Duc Minh Vu
ACPO: AI-Enabled Compiler-Driven Program Optimization
Dec 15, 2023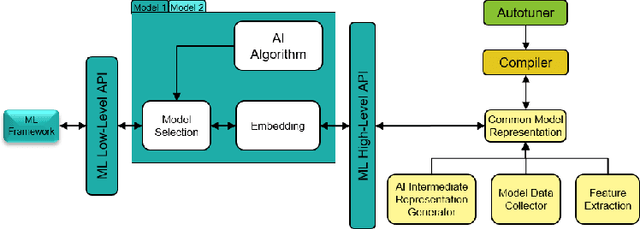
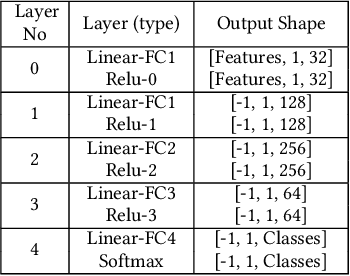
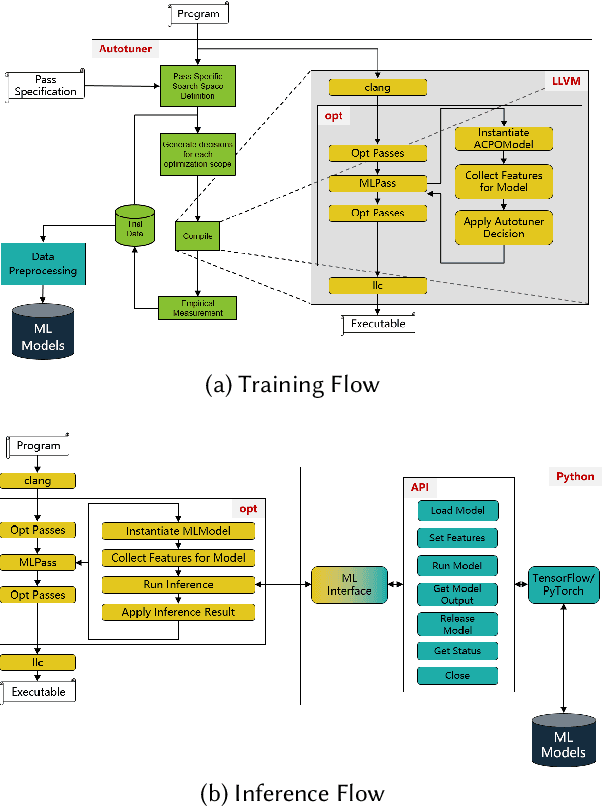
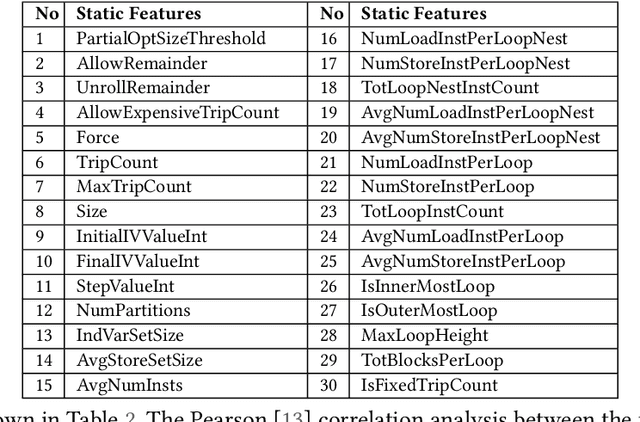
Abstract:The key to performance optimization of a program is to decide correctly when a certain transformation should be applied by a compiler. Traditionally, such profitability decisions are made by hand-coded algorithms tuned for a very small number of benchmarks, usually requiring a great deal of effort to be retuned when the benchmark suite changes. This is an ideal opportunity to apply machine-learning models to speed up the tuning process; while this realization has been around since the late 90s, only recent advancements in ML enabled a practical application of ML to compilers as an end-to-end framework. Even so, seamless integration of ML into the compiler would require constant rebuilding of the compiler when models are updated. This paper presents ACPO: \textbf{\underline{A}}I-Enabled \textbf{\underline{C}}ompiler-driven \textbf{\underline{P}}rogram \textbf{\underline{O}}ptimization; a novel framework to provide LLVM with simple and comprehensive tools to benefit from employing ML models for different optimization passes. We first showcase the high-level view, class hierarchy, and functionalities of ACPO and subsequently, demonstrate \taco{a couple of use cases of ACPO by ML-enabling the Loop Unroll and Function Inlining passes and describe how ACPO can be leveraged to optimize other passes. Experimental results reveal that ACPO model for Loop Unroll is able to gain on average 4\% and 3\%, 5.4\%, 0.2\% compared to LLVM's O3 optimization when deployed on Polybench, Coral-2, CoreMark, and Graph-500, respectively. Furthermore, by adding the Inliner model as well, ACPO is able to provide up to 4.5\% and 2.4\% on Polybench and Cbench compared with LLVM's O3 optimization, respectively.
A* search algorithm for an optimal investment problem in vehicle-sharing systems
Nov 15, 2023Abstract:We study an optimal investment problem that arises in the context of the vehicle-sharing system. Given a set of locations to build stations, we need to determine i) the sequence of stations to be built and the number of vehicles to acquire in order to obtain the target state where all stations are built, and ii) the number of vehicles to acquire and their allocation in order to maximize the total profit returned by operating the system when some or all stations are open. The profitability associated with operating open stations, measured over a specific time period, is represented as a linear optimization problem applied to a collection of open stations. With operating capital, the owner of the system can open new stations. This property introduces a set-dependent aspect to the duration required for opening a new station, and the optimal investment problem can be viewed as a variant of the Traveling Salesman Problem (TSP) with set-dependent cost. We propose an A* search algorithm to address this particular variant of the TSP. Computational experiments highlight the benefits of the proposed algorithm in comparison to the widely recognized Dijkstra algorithm and propose future research to explore new possibilities and applications for both exact and approximate A* algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge