Maximizing Conditional Entropy for Batch-Mode Active Learning of Perceptual Metrics
Paper and Code
Mar 16, 2021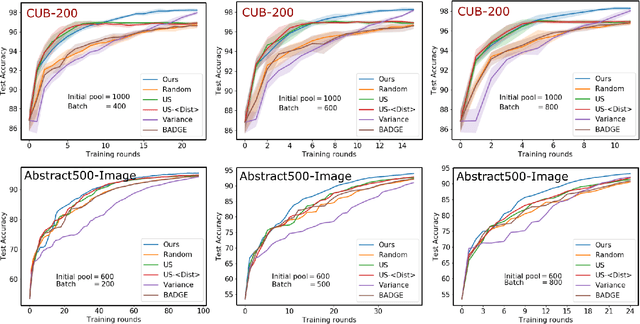
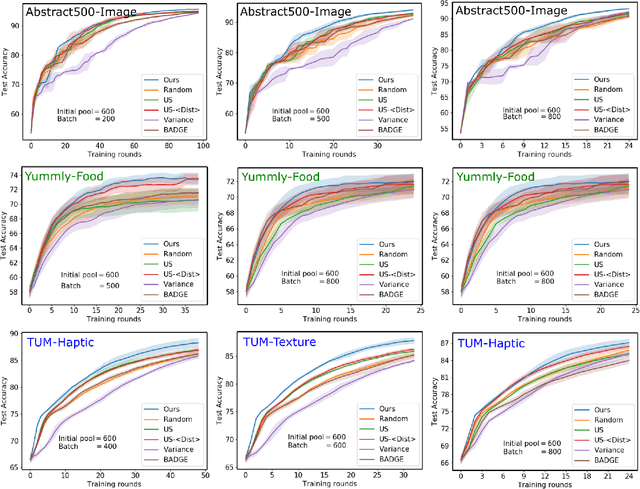
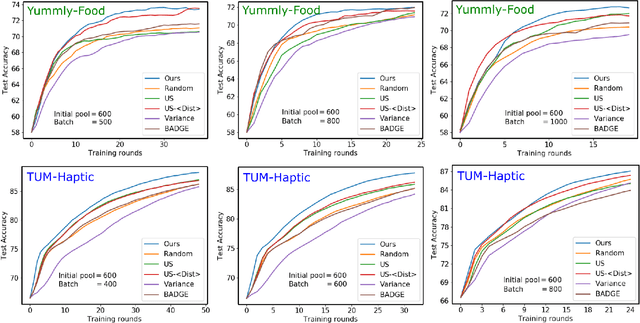
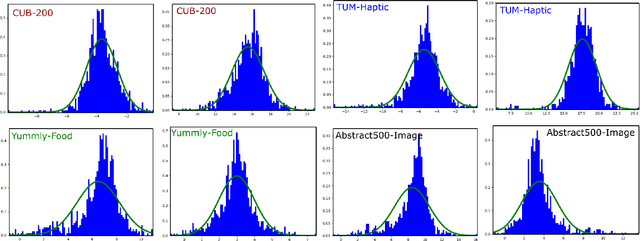
Active metric learning is the problem of incrementally selecting batches of training data (typically, ordered triplets) to annotate, in order to progressively improve a learned model of a metric over some input domain as rapidly as possible. Standard approaches, which independently select each triplet in a batch, are susceptible to highly correlated batches with many redundant triplets and hence low overall utility. While there has been recent work on selecting decorrelated batches for metric learning \cite{kumari2020batch}, these methods rely on ad hoc heuristics to estimate the correlation between two triplets at a time. We present a novel approach for batch mode active metric learning using the Maximum Entropy Principle that seeks to collectively select batches with maximum joint entropy, which captures both the informativeness and the diversity of the triplets. The entropy is derived from the second-order statistics estimated by dropout. We take advantage of the monotonically increasing submodular entropy function to construct an efficient greedy algorithm based on Gram-Schmidt orthogonalization that is provably $\left( 1 - \frac{1}{e} \right)$-optimal. Our approach is the first batch-mode active metric learning method to define a unified score that balances informativeness and diversity for an entire batch of triplets. Experiments with several real-world datasets demonstrate that our algorithm is robust and consistently outperforms the state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge