DECOLLAGE: 3D Detailization by Controllable, Localized, and Learned Geometry Enhancement

We present a 3D modeling method which enables end-users to refine or detailize 3D shapes using machine learning, expanding the capabilities of AI-assisted 3D content creation. Given a coarse voxel shape (e.g., one produced with a simple box extrusion tool or via generative modeling), a user can directly "paint" desired target styles representing compelling geometric details, from input exemplar shapes, over different regions of the coarse shape. These regions are then up-sampled into high-resolution geometries which adhere with the painted styles. To achieve such controllable and localized 3D detailization, we build on top of a Pyramid GAN by making it masking-aware. We devise novel structural losses and priors to ensure that our method preserves both desired coarse structures and fine-grained features even if the painted styles are borrowed from diverse sources, e.g., different semantic parts and even different shape categories. Through extensive experiments, we show that our ability to localize details enables novel interactive creative workflows and applications. Our experiments further demonstrate that in comparison to prior techniques built on global detailization, our method generates structure-preserving, high-resolution stylized geometries with more coherent shape details and style transitions.

Temporal Residual Jacobians For Rig-free Motion Transfer

We introduce Temporal Residual Jacobians as a novel representation to enable data-driven motion transfer. Our approach does not assume access to any rigging or intermediate shape keyframes, produces geometrically and temporally consistent motions, and can be used to transfer long motion sequences. Central to our approach are two coupled neural networks that individually predict local geometric and temporal changes that are subsequently integrated, spatially and temporally, to produce the final animated meshes. The two networks are jointly trained, complement each other in producing spatial and temporal signals, and are supervised directly with 3D positional information. During inference, in the absence of keyframes, our method essentially solves a motion extrapolation problem. We test our setup on diverse meshes (synthetic and scanned shapes) to demonstrate its superiority in generating realistic and natural-looking animations on unseen body shapes against SoTA alternatives. Supplemental video and code are available at https://temporaljacobians.github.io/ .

Learning to Infer Generative Template Programs for Visual Concepts

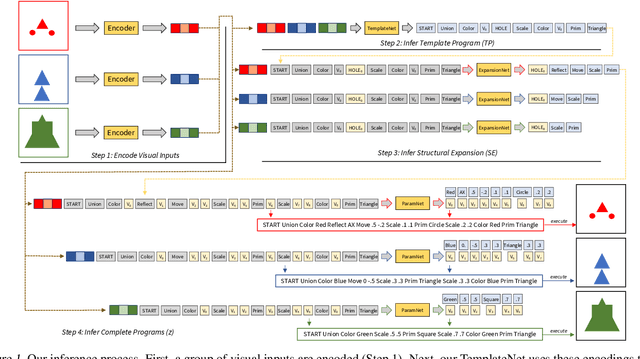
People grasp flexible visual concepts from a few examples. We explore a neurosymbolic system that learns how to infer programs that capture visual concepts in a domain-general fashion. We introduce Template Programs: programmatic expressions from a domain-specific language that specify structural and parametric patterns common to an input concept. Our framework supports multiple concept-related tasks, including few-shot generation and co-segmentation through parsing. We develop a learning paradigm that allows us to train networks that infer Template Programs directly from visual datasets that contain concept groupings. We run experiments across multiple visual domains: 2D layouts, Omniglot characters, and 3D shapes. We find that our method outperforms task-specific alternatives, and performs competitively against domain-specific approaches for the limited domains where they exist.

GEM3D: GEnerative Medial Abstractions for 3D Shape Synthesis

We introduce GEM3D -- a new deep, topology-aware generative model of 3D shapes. The key ingredient of our method is a neural skeleton-based representation encoding information on both shape topology and geometry. Through a denoising diffusion probabilistic model, our method first generates skeleton-based representations following the Medial Axis Transform (MAT), then generates surfaces through a skeleton-driven neural implicit formulation. The neural implicit takes into account the topological and geometric information stored in the generated skeleton representations to yield surfaces that are more topologically and geometrically accurate compared to previous neural field formulations. We discuss applications of our method in shape synthesis and point cloud reconstruction tasks, and evaluate our method both qualitatively and quantitatively. We demonstrate significantly more faithful surface reconstruction and diverse shape generation results compared to the state-of-the-art, also involving challenging scenarios of reconstructing and synthesizing structurally complex, high-genus shape surfaces from Thingi10K and ShapeNet.

Explorable Mesh Deformation Subspaces from Unstructured Generative Models

Exploring variations of 3D shapes is a time-consuming process in traditional 3D modeling tools. Deep generative models of 3D shapes often feature continuous latent spaces that can, in principle, be used to explore potential variations starting from a set of input shapes. In practice, doing so can be problematic: latent spaces are high dimensional and hard to visualize, contain shapes that are not relevant to the input shapes, and linear paths through them often lead to sub-optimal shape transitions. Furthermore, one would ideally be able to explore variations in the original high-quality meshes used to train the generative model, not its lower-quality output geometry. In this paper, we present a method to explore variations among a given set of landmark shapes by constructing a mapping from an easily-navigable 2D exploration space to a subspace of a pre-trained generative model. We first describe how to find a mapping that spans the set of input landmark shapes and exhibits smooth variations between them. We then show how to turn the variations in this subspace into deformation fields, to transfer those variations to high-quality meshes for the landmark shapes. Our results show that our method can produce visually-pleasing and easily-navigable 2D exploration spaces for several different shape categories, especially as compared to prior work on learning deformation spaces for 3D shapes.

Unsupervised 3D Shape Reconstruction by Part Retrieval and Assembly

Representing a 3D shape with a set of primitives can aid perception of structure, improve robotic object manipulation, and enable editing, stylization, and compression of 3D shapes. Existing methods either use simple parametric primitives or learn a generative shape space of parts. Both have limitations: parametric primitives lead to coarse approximations, while learned parts offer too little control over the decomposition. We instead propose to decompose shapes using a library of 3D parts provided by the user, giving full control over the choice of parts. The library can contain parts with high-quality geometry that are suitable for a given category, resulting in meaningful decompositions with clean geometry. The type of decomposition can also be controlled through the choice of parts in the library. Our method works via a self-supervised approach that iteratively retrieves parts from the library and refines their placements. We show that this approach gives higher reconstruction accuracy and more desirable decompositions than existing approaches. Additionally, we show how the decomposition can be controlled through the part library by using different part libraries to reconstruct the same shapes.

PatchRD: Detail-Preserving Shape Completion by Learning Patch Retrieval and Deformation

This paper introduces a data-driven shape completion approach that focuses on completing geometric details of missing regions of 3D shapes. We observe that existing generative methods lack the training data and representation capacity to synthesize plausible, fine-grained details with complex geometry and topology. Our key insight is to copy and deform patches from the partial input to complete missing regions. This enables us to preserve the style of local geometric features, even if it drastically differs from the training data. Our fully automatic approach proceeds in two stages. First, we learn to retrieve candidate patches from the input shape. Second, we select and deform some of the retrieved candidates to seamlessly blend them into the complete shape. This method combines the advantages of the two most common completion methods: similarity-based single-instance completion, and completion by learning a shape space. We leverage repeating patterns by retrieving patches from the partial input, and learn global structural priors by using a neural network to guide the retrieval and deformation steps. Experimental results show our approach considerably outperforms baselines across multiple datasets and shape categories. Code and data are available at https://github.com/GitBoSun/PatchRD.

Neural Jacobian Fields: Learning Intrinsic Mappings of Arbitrary Meshes

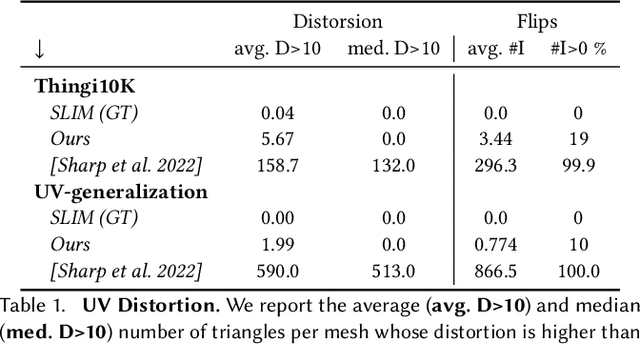
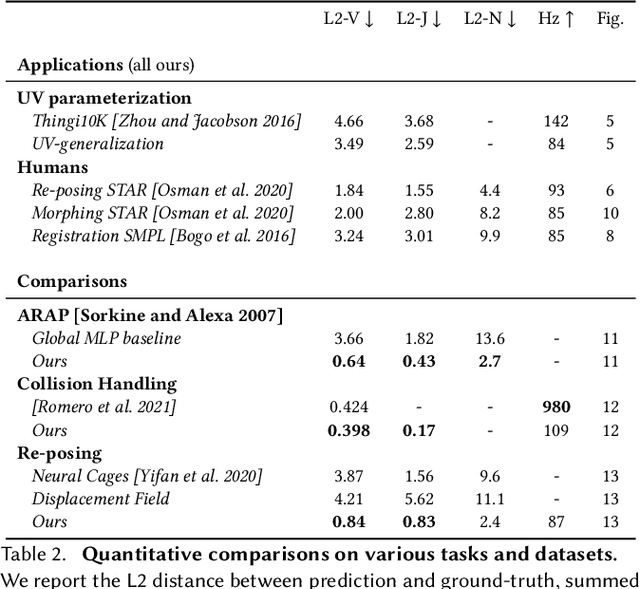
This paper introduces a framework designed to accurately predict piecewise linear mappings of arbitrary meshes via a neural network, enabling training and evaluating over heterogeneous collections of meshes that do not share a triangulation, as well as producing highly detail-preserving maps whose accuracy exceeds current state of the art. The framework is based on reducing the neural aspect to a prediction of a matrix for a single given point, conditioned on a global shape descriptor. The field of matrices is then projected onto the tangent bundle of the given mesh, and used as candidate jacobians for the predicted map. The map is computed by a standard Poisson solve, implemented as a differentiable layer with cached pre-factorization for efficient training. This construction is agnostic to the triangulation of the input, thereby enabling applications on datasets with varying triangulations. At the same time, by operating in the intrinsic gradient domain of each individual mesh, it allows the framework to predict highly-accurate mappings. We validate these properties by conducting experiments over a broad range of scenarios, from semantic ones such as morphing, registration, and deformation transfer, to optimization-based ones, such as emulating elastic deformations and contact correction, as well as being the first work, to our knowledge, to tackle the task of learning to compute UV parameterizations of arbitrary meshes. The results exhibit the high accuracy of the method as well as its versatility, as it is readily applied to the above scenarios without any changes to the framework.

The Shape Part Slot Machine: Contact-based Reasoning for Generating 3D Shapes from Parts

We present the Shape Part Slot Machine, a new method for assembling novel 3D shapes from existing parts by performing contact-based reasoning. Our method represents each shape as a graph of "slots," where each slot is a region of contact between two shape parts. Based on this representation, we design a graph-neural-network-based model for generating new slot graphs and retrieving compatible parts, as well as a gradient-descent-based optimization scheme for assembling the retrieved parts into a complete shape that respects the generated slot graph. This approach does not require any semantic part labels; interestingly, it also does not require complete part geometries -- reasoning about the regions where parts connect proves sufficient to generate novel, high-quality 3D shapes. We demonstrate that our method generates shapes that outperform existing modeling-by-assembly approaches in terms of quality, diversity, and structural complexity.

ReGroup: Recursive Neural Networks for Hierarchical Grouping of Vector Graphic Primitives

Selection functionality is as fundamental to vector graphics as it is for raster data. But vector selection is quite different: instead of pixel-level labeling, we make a binary decision to include or exclude each vector primitive. In the absence of intelligible metadata, this becomes a perceptual grouping problem. These have previously relied on heuristics derived from empirical principles like Gestalt Theory, but since these are ill-defined and subjective, they often result in ambiguity. Here we take a data-centric approach to the problem. By exploiting the recursive nature of perceptual grouping, we interpret the task as constructing a hierarchy over the primitives of a vector graphic, which is amenable to learning with recursive neural networks with few human annotations. We verify this by building a dataset of these hierarchies on which we train a hierarchical grouping network. We then demonstrate how this can underpin a prototype selection tool.