Residual Primitive Fitting of 3D Shapes with SuperFrusta

We introduce a framework for converting 3D shapes into compact and editable assemblies of analytic primitives, directly addressing the persistent trade-off between reconstruction fidelity and parsimony. Our approach combines two key contributions: a novel primitive, termed SuperFrustum, and an iterative fiting algorithm, Residual Primitive Fitting (ResFit). SuperFrustum is an analytical primitive that is simultaneously (1) expressive, being able to model various common solids such as cylinders, spheres, cones & their tapered and bent forms, (2) editable, being compactly parameterized with 8 parameters, and (3) optimizable, with a sign distance field differentiable w.r.t. its parameters almost everywhere. ResFit is an unsupervised procedure that interleaves global shape analysis with local optimization, iteratively fitting primitives to the unexplained residual of a shape to discover a parsimonious yet accurate decompositions for each input shape. On diverse 3D benchmarks, our method achieves state-of-the-art results, improving IoU by over 9 points while using nearly half as many primitives as prior work. The resulting assemblies bridge the gap between dense 3D data and human-controllable design, producing high-fidelity and editable shape programs.

ART-DECO: Arbitrary Text Guidance for 3D Detailizer Construction

We introduce a 3D detailizer, a neural model which can instantaneously (in <1s) transform a coarse 3D shape proxy into a high-quality asset with detailed geometry and texture as guided by an input text prompt. Our model is trained using the text prompt, which defines the shape class and characterizes the appearance and fine-grained style of the generated details. The coarse 3D proxy, which can be easily varied and adjusted (e.g., via user editing), provides structure control over the final shape. Importantly, our detailizer is not optimized for a single shape; it is the result of distilling a generative model, so that it can be reused, without retraining, to generate any number of shapes, with varied structures, whose local details all share a consistent style and appearance. Our detailizer training utilizes a pretrained multi-view image diffusion model, with text conditioning, to distill the foundational knowledge therein into our detailizer via Score Distillation Sampling (SDS). To improve SDS and enable our detailizer architecture to learn generalizable features over complex structures, we train our model in two training stages to generate shapes with increasing structural complexity. Through extensive experiments, we show that our method generates shapes of superior quality and details compared to existing text-to-3D models under varied structure control. Our detailizer can refine a coarse shape in less than a second, making it possible to interactively author and adjust 3D shapes. Furthermore, the user-imposed structure control can lead to creative, and hence out-of-distribution, 3D asset generations that are beyond the current capabilities of leading text-to-3D generative models. We demonstrate an interactive 3D modeling workflow our method enables, and its strong generalizability over styles, structures, and object categories.

DECOLLAGE: 3D Detailization by Controllable, Localized, and Learned Geometry Enhancement

We present a 3D modeling method which enables end-users to refine or detailize 3D shapes using machine learning, expanding the capabilities of AI-assisted 3D content creation. Given a coarse voxel shape (e.g., one produced with a simple box extrusion tool or via generative modeling), a user can directly "paint" desired target styles representing compelling geometric details, from input exemplar shapes, over different regions of the coarse shape. These regions are then up-sampled into high-resolution geometries which adhere with the painted styles. To achieve such controllable and localized 3D detailization, we build on top of a Pyramid GAN by making it masking-aware. We devise novel structural losses and priors to ensure that our method preserves both desired coarse structures and fine-grained features even if the painted styles are borrowed from diverse sources, e.g., different semantic parts and even different shape categories. Through extensive experiments, we show that our ability to localize details enables novel interactive creative workflows and applications. Our experiments further demonstrate that in comparison to prior techniques built on global detailization, our method generates structure-preserving, high-resolution stylized geometries with more coherent shape details and style transitions.

Text-guided Controllable Mesh Refinement for Interactive 3D Modeling

We propose a novel technique for adding geometric details to an input coarse 3D mesh guided by a text prompt. Our method is composed of three stages. First, we generate a single-view RGB image conditioned on the input coarse geometry and the input text prompt. This single-view image generation step allows the user to pre-visualize the result and offers stronger conditioning for subsequent multi-view generation. Second, we use our novel multi-view normal generation architecture to jointly generate six different views of the normal images. The joint view generation reduces inconsistencies and leads to sharper details. Third, we optimize our mesh with respect to all views and generate a fine, detailed geometry as output. The resulting method produces an output within seconds and offers explicit user control over the coarse structure, pose, and desired details of the resulting 3D mesh. Project page: https://text-mesh-refinement.github.io.

DAE-Net: Deforming Auto-Encoder for fine-grained shape co-segmentation

We present an unsupervised 3D shape co-segmentation method which learns a set of deformable part templates from a shape collection. To accommodate structural variations in the collection, our network composes each shape by a selected subset of template parts which are affine-transformed. To maximize the expressive power of the part templates, we introduce a per-part deformation network to enable the modeling of diverse parts with substantial geometry variations, while imposing constraints on the deformation capacity to ensure fidelity to the originally represented parts. We also propose a training scheme to effectively overcome local minima. Architecturally, our network is a branched autoencoder, with a CNN encoder taking a voxel shape as input and producing per-part transformation matrices, latent codes, and part existence scores, and the decoder outputting point occupancies to define the reconstruction loss. Our network, coined DAE-Net for Deforming Auto-Encoder, can achieve unsupervised 3D shape co-segmentation that yields fine-grained, compact, and meaningful parts that are consistent across diverse shapes. We conduct extensive experiments on the ShapeNet Part dataset, DFAUST, and an animal subset of Objaverse to show superior performance over prior methods.

ShaDDR: Real-Time Example-Based Geometry and Texture Generation via 3D Shape Detailization and Differentiable Rendering

We present ShaDDR, an example-based deep generative neural network which produces a high-resolution textured 3D shape through geometry detailization and conditional texture generation applied to an input coarse voxel shape. Trained on a small set of detailed and textured exemplar shapes, our method learns to detailize the geometry via multi-resolution voxel upsampling and generate textures on voxel surfaces via differentiable rendering against exemplar texture images from a few views. The generation is real-time, taking less than 1 second to produce a 3D model with voxel resolutions up to 512^3. The generated shape preserves the overall structure of the input coarse voxel model, while the style of the generated geometric details and textures can be manipulated through learned latent codes. In the experiments, we show that our method can generate higher-resolution shapes with plausible and improved geometric details and clean textures compared to prior works. Furthermore, we showcase the ability of our method to learn geometric details and textures from shapes reconstructed from real-world photos. In addition, we have developed an interactive modeling application to demonstrate the generalizability of our method to various user inputs and the controllability it offers, allowing users to interactively sculpt a coarse voxel shape to define the overall structure of the detailized 3D shape.

A Review of Deep Learning-Powered Mesh Reconstruction Methods

With the recent advances in hardware and rendering techniques, 3D models have emerged everywhere in our life. Yet creating 3D shapes is arduous and requires significant professional knowledge. Meanwhile, Deep learning has enabled high-quality 3D shape reconstruction from various sources, making it a viable approach to acquiring 3D shapes with minimal effort. Importantly, to be used in common 3D applications, the reconstructed shapes need to be represented as polygonal meshes, which is a challenge for neural networks due to the irregularity of mesh tessellations. In this survey, we provide a comprehensive review of mesh reconstruction methods that are powered by machine learning. We first describe various representations for 3D shapes in the deep learning context. Then we review the development of 3D mesh reconstruction methods from voxels, point clouds, single images, and multi-view images. Finally, we identify several challenges in this field and propose potential future directions.

MobileNeRF: Exploiting the Polygon Rasterization Pipeline for Efficient Neural Field Rendering on Mobile Architectures

Neural Radiance Fields (NeRFs) have demonstrated amazing ability to synthesize images of 3D scenes from novel views. However, they rely upon specialized volumetric rendering algorithms based on ray marching that are mismatched to the capabilities of widely deployed graphics hardware. This paper introduces a new NeRF representation based on textured polygons that can synthesize novel images efficiently with standard rendering pipelines. The NeRF is represented as a set of polygons with textures representing binary opacities and feature vectors. Traditional rendering of the polygons with a z-buffer yields an image with features at every pixel, which are interpreted by a small, view-dependent MLP running in a fragment shader to produce a final pixel color. This approach enables NeRFs to be rendered with the traditional polygon rasterization pipeline, which provides massive pixel-level parallelism, achieving interactive frame rates on a wide range of compute platforms, including mobile phones.

AUV-Net: Learning Aligned UV Maps for Texture Transfer and Synthesis

In this paper, we address the problem of texture representation for 3D shapes for the challenging and underexplored tasks of texture transfer and synthesis. Previous works either apply spherical texture maps which may lead to large distortions, or use continuous texture fields that yield smooth outputs lacking details. We argue that the traditional way of representing textures with images and linking them to a 3D mesh via UV mapping is more desirable, since synthesizing 2D images is a well-studied problem. We propose AUV-Net which learns to embed 3D surfaces into a 2D aligned UV space, by mapping the corresponding semantic parts of different 3D shapes to the same location in the UV space. As a result, textures are aligned across objects, and can thus be easily synthesized by generative models of images. Texture alignment is learned in an unsupervised manner by a simple yet effective texture alignment module, taking inspiration from traditional works on linear subspace learning. The learned UV mapping and aligned texture representations enable a variety of applications including texture transfer, texture synthesis, and textured single view 3D reconstruction. We conduct experiments on multiple datasets to demonstrate the effectiveness of our method. Project page: https://nv-tlabs.github.io/AUV-NET.

Neural Dual Contouring

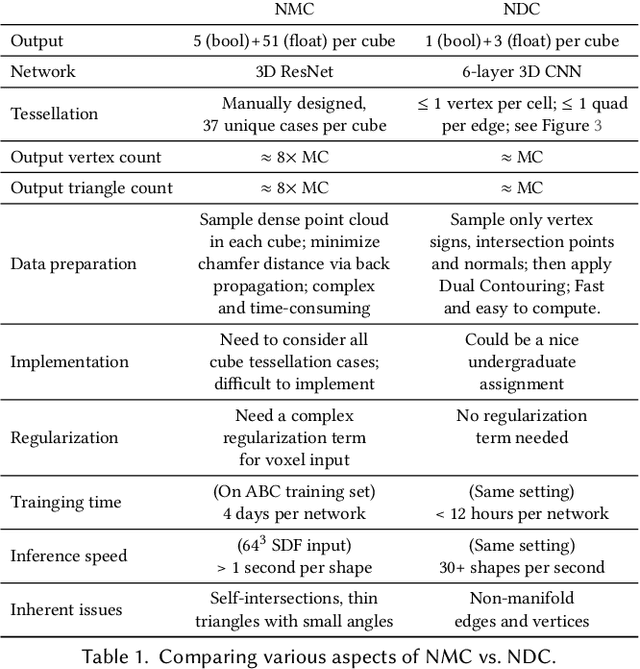
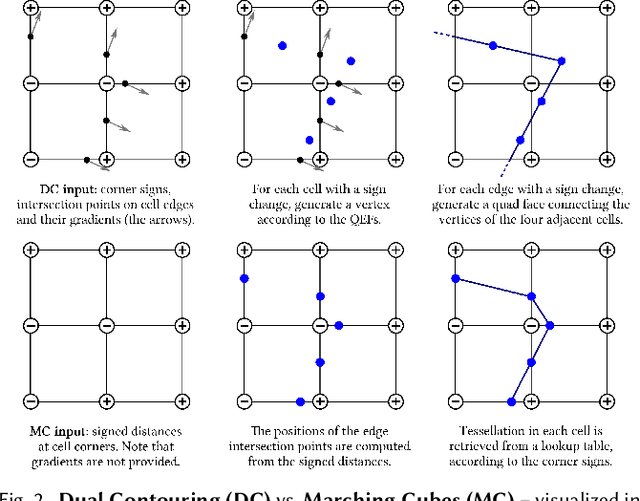
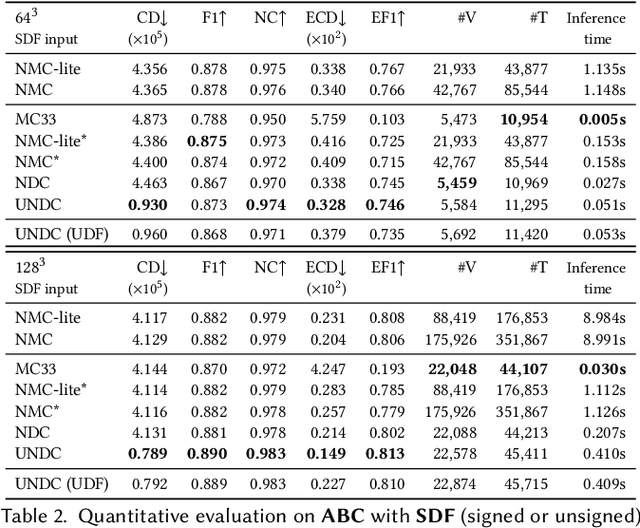
We introduce neural dual contouring (NDC), a new data-driven approach to mesh reconstruction based on dual contouring (DC). Like traditional DC, it produces exactly one vertex per grid cell and one quad for each grid edge intersection, a natural and efficient structure for reproducing sharp features. However, rather than computing vertex locations and edge crossings with hand-crafted functions that depend directly on difficult-to-obtain surface gradients, NDC uses a neural network to predict them. As a result, NDC can be trained to produce meshes from signed or unsigned distance fields, binary voxel grids, or point clouds (with or without normals); and it can produce open surfaces in cases where the input represents a sheet or partial surface. During experiments with five prominent datasets, we find that NDC, when trained on one of the datasets, generalizes well to the others. Furthermore, NDC provides better surface reconstruction accuracy, feature preservation, output complexity, triangle quality, and inference time in comparison to previous learned (e.g., neural marching cubes, convolutional occupancy networks) and traditional (e.g., Poisson) methods.