Learning Mesh Representations via Binary Space Partitioning Tree Networks
Paper and Code
Jul 02, 2021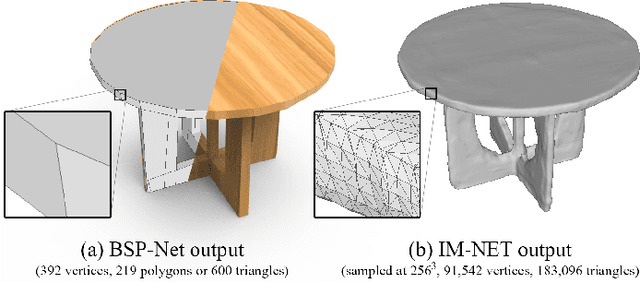


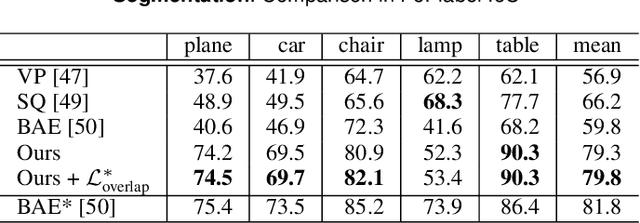
Polygonal meshes are ubiquitous, but have only played a relatively minor role in the deep learning revolution. State-of-the-art neural generative models for 3D shapes learn implicit functions and generate meshes via expensive iso-surfacing. We overcome these challenges by employing a classical spatial data structure from computer graphics, Binary Space Partitioning (BSP), to facilitate 3D learning. The core operation of BSP involves recursive subdivision of 3D space to obtain convex sets. By exploiting this property, we devise BSP-Net, a network that learns to represent a 3D shape via convex decomposition without supervision. The network is trained to reconstruct a shape using a set of convexes obtained from a BSP-tree built over a set of planes, where the planes and convexes are both defined by learned network weights. BSP-Net directly outputs polygonal meshes from the inferred convexes. The generated meshes are watertight, compact (i.e., low-poly), and well suited to represent sharp geometry. We show that the reconstruction quality by BSP-Net is competitive with those from state-of-the-art methods while using much fewer primitives. We also explore variations to BSP-Net including using a more generic decoder for reconstruction, more general primitives than planes, as well as training a generative model with variational auto-encoders. Code is available at https://github.com/czq142857/BSP-NET-original.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge