Quantifying Normality: Convergence Rate to Gaussian Limit for Stochastic Approximation and Unadjusted OU Algorithm

Stochastic approximation (SA) is a method for finding the root of an operator perturbed by noise. There is a rich literature establishing the asymptotic normality of rescaled SA iterates under fairly mild conditions. However, these asymptotic results do not quantify the accuracy of the Gaussian approximation in finite time. In this paper, we establish explicit non-asymptotic bounds on the Wasserstein distance between the distribution of the rescaled iterate at time k and the asymptotic Gaussian limit for various choices of step-sizes including constant and polynomially decaying. As an immediate consequence, we obtain tail bounds on the error of SA iterates at any time. We obtain the sharp rates by first studying the convergence rate of the discrete Ornstein-Uhlenbeck (O-U) process driven by general noise, whose stationary distribution is identical to the limiting Gaussian distribution of the rescaled SA iterates. We believe that this is of independent interest, given its connection to sampling literature. The analysis involves adapting Stein's method for Gaussian approximation to handle the matrix weighted sum of i.i.d. random variables. The desired finite-time bounds for SA are obtained by characterizing the error dynamics between the rescaled SA iterate and the discrete time O-U process and combining it with the convergence rate of the latter process.

A Non-Asymptotic Theory of Seminorm Lyapunov Stability: From Deterministic to Stochastic Iterative Algorithms

We study the problem of solving fixed-point equations for seminorm-contractive operators and establish foundational results on the non-asymptotic behavior of iterative algorithms in both deterministic and stochastic settings. Specifically, in the deterministic setting, we prove a fixed-point theorem for seminorm-contractive operators, showing that iterates converge geometrically to the kernel of the seminorm. In the stochastic setting, we analyze the corresponding stochastic approximation (SA) algorithm under seminorm-contractive operators and Markovian noise, providing a finite-sample analysis for various stepsize choices. A benchmark for equation solving is linear systems of equations, where the convergence behavior of fixed-point iteration is closely tied to the stability of linear dynamical systems. In this special case, our results provide a complete characterization of system stability with respect to a seminorm, linking it to the solution of a Lyapunov equation in terms of positive semi-definite matrices. In the stochastic setting, we establish a finite-sample analysis for linear Markovian SA without requiring the Hurwitzness assumption. Our theoretical results offer a unified framework for deriving finite-sample bounds for various reinforcement learning algorithms in the average reward setting, including TD($\lambda$) for policy evaluation (which is a special case of solving a Poisson equation) and Q-learning for control.

Stochastic Approximation with Unbounded Markovian Noise: A General-Purpose Theorem

Motivated by engineering applications such as resource allocation in networks and inventory systems, we consider average-reward Reinforcement Learning with unbounded state space and reward function. Recent works studied this problem in the actor-critic framework and established finite sample bounds assuming access to a critic with certain error guarantees. We complement their work by studying Temporal Difference (TD) learning with linear function approximation and establishing finite-time bounds with the optimal $\mathcal{O}\left(1/\epsilon^2\right)$ sample complexity. These results are obtained using the following general-purpose theorem for non-linear Stochastic Approximation (SA). Suppose that one constructs a Lyapunov function for a non-linear SA with certain drift condition. Then, our theorem establishes finite-time bounds when this SA is driven by unbounded Markovian noise under suitable conditions. It serves as a black box tool to generalize sample guarantees on SA from i.i.d. or martingale difference case to potentially unbounded Markovian noise. The generality and the mild assumption of the setup enables broad applicability of our theorem. We illustrate its power by studying two more systems: (i) We improve upon the finite-time bounds of $Q$-learning by tightening the error bounds and also allowing for a larger class of behavior policies. (ii) We establish the first ever finite-time bounds for distributed stochastic optimization of high-dimensional smooth strongly convex function using cyclic block coordinate descent.

Tight Finite Time Bounds of Two-Time-Scale Linear Stochastic Approximation with Markovian Noise

Stochastic approximation (SA) is an iterative algorithm to find the fixed point of an operator given noisy samples of this operator. SA appears in many areas such as optimization and Reinforcement Learning (RL). When implemented in practice, the noise that appears in the update of RL algorithms is naturally Markovian. Furthermore, in some settings, such as gradient TD, SA is employed in a two-time-scale manner. The mix of Markovian noise along with the two-time-scale structure results in an algorithm which is complex to analyze theoretically. In this paper, we characterize a tight convergence bound for the iterations of linear two-time-scale SA with Markovian noise. Our results show the convergence behavior of this algorithm given various choices of step sizes. Applying our result to the well-known TDC algorithm, we show the first $O(1/\epsilon)$ sample complexity for the convergence of this algorithm, outperforming all the previous work. Similarly, our results can be applied to establish the convergence behavior of a variety of RL algorithms, such as TD-learning with Polyak averaging, GTD, and GTD2.

Concentration bounds for SSP Q-learning for average cost MDPs

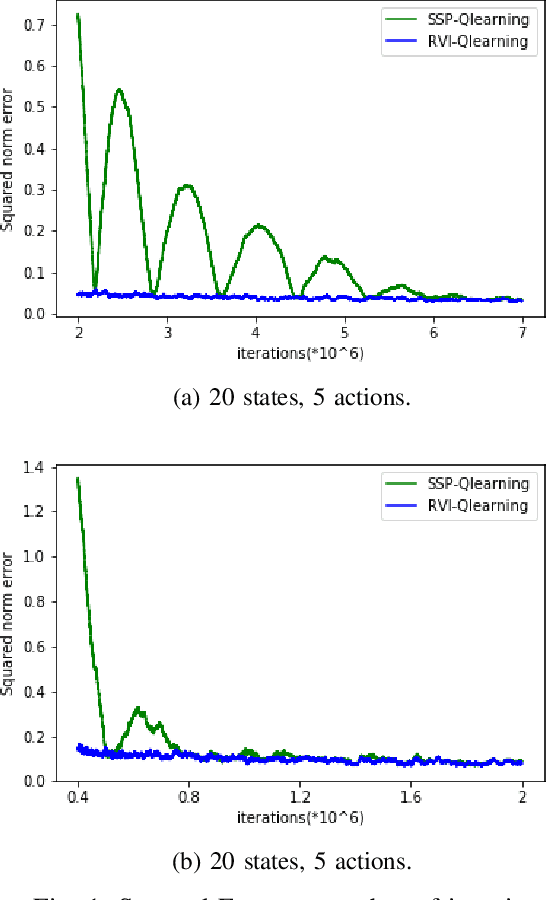
We derive a concentration bound for a Q-learning algorithm for average cost Markov decision processes based on an equivalent shortest path problem, and compare it numerically with the alternative scheme based on relative value iteration.