Leveraging High-Fidelity Digital Models and Reinforcement Learning for Mission Engineering: A Case Study of Aerial Firefighting Under Perfect Information

As systems engineering (SE) objectives evolve from design and operation of monolithic systems to complex System of Systems (SoS), the discipline of Mission Engineering (ME) has emerged which is increasingly being accepted as a new line of thinking for the SE community. Moreover, mission environments are uncertain, dynamic, and mission outcomes are a direct function of how the mission assets will interact with this environment. This proves static architectures brittle and calls for analytically rigorous approaches for ME. To that end, this paper proposes an intelligent mission coordination methodology that integrates digital mission models with Reinforcement Learning (RL), that specifically addresses the need for adaptive task allocation and reconfiguration. More specifically, we are leveraging a Digital Engineering (DE) based infrastructure that is composed of a high-fidelity digital mission model and agent-based simulation; and then we formulate the mission tactics management problem as a Markov Decision Process (MDP), and employ an RL agent trained via Proximal Policy Optimization. By leveraging the simulation as a sandbox, we map the system states to actions, refining the policy based on realized mission outcomes. The utility of the RL-based intelligent mission coordinator is demonstrated through an aerial firefighting case study. Our findings indicate that the RL-based intelligent mission coordinator not only surpasses baseline performance but also significantly reduces the variability in mission performance. Thus, this study serves as a proof of concept demonstrating that DE-enabled mission simulations combined with advanced analytical tools offer a mission-agnostic framework for improving ME practice; which can be extended to more complicated fleet design and selection problems in the future from a mission-first perspective.

Optimistic Reinforcement Learning with Quantile Objectives

Reinforcement Learning (RL) has achieved tremendous success in recent years. However, the classical foundations of RL do not account for the risk sensitivity of the objective function, which is critical in various fields, including healthcare and finance. A popular approach to incorporate risk sensitivity is to optimize a specific quantile of the cumulative reward distribution. In this paper, we develop UCB-QRL, an optimistic learning algorithm for the $τ$-quantile objective in finite-horizon Markov decision processes (MDPs). UCB-QRL is an iterative algorithm in which, at each iteration, we first estimate the underlying transition probability and then optimize the quantile value function over a confidence ball around this estimate. We show that UCB-QRL yields a high-probability regret bound $\mathcal O\left((2/κ)^{H+1}H\sqrt{SATH\log(2SATH/δ)}\right)$ in the episodic setting with $S$ states, $A$ actions, $T$ episodes, and $H$ horizons. Here, $κ>0$ is a problem-dependent constant that captures the sensitivity of the underlying MDP's quantile value.

A General-Purpose Theorem for High-Probability Bounds of Stochastic Approximation with Polyak Averaging

Polyak-Ruppert averaging is a widely used technique to achieve the optimal asymptotic variance of stochastic approximation (SA) algorithms, yet its high-probability performance guarantees remain underexplored in general settings. In this paper, we present a general framework for establishing non-asymptotic concentration bounds for the error of averaged SA iterates. Our approach assumes access to individual concentration bounds for the unaveraged iterates and yields a sharp bound on the averaged iterates. We also construct an example, showing the tightness of our result up to constant multiplicative factors. As direct applications, we derive tight concentration bounds for contractive SA algorithms and for algorithms such as temporal difference learning and Q-learning with averaging, obtaining new bounds in settings where traditional analysis is challenging.

Tight Finite Time Bounds of Two-Time-Scale Linear Stochastic Approximation with Markovian Noise

Stochastic approximation (SA) is an iterative algorithm to find the fixed point of an operator given noisy samples of this operator. SA appears in many areas such as optimization and Reinforcement Learning (RL). When implemented in practice, the noise that appears in the update of RL algorithms is naturally Markovian. Furthermore, in some settings, such as gradient TD, SA is employed in a two-time-scale manner. The mix of Markovian noise along with the two-time-scale structure results in an algorithm which is complex to analyze theoretically. In this paper, we characterize a tight convergence bound for the iterations of linear two-time-scale SA with Markovian noise. Our results show the convergence behavior of this algorithm given various choices of step sizes. Applying our result to the well-known TDC algorithm, we show the first $O(1/\epsilon)$ sample complexity for the convergence of this algorithm, outperforming all the previous work. Similarly, our results can be applied to establish the convergence behavior of a variety of RL algorithms, such as TD-learning with Polyak averaging, GTD, and GTD2.

Federated Reinforcement Learning: Linear Speedup Under Markovian Sampling

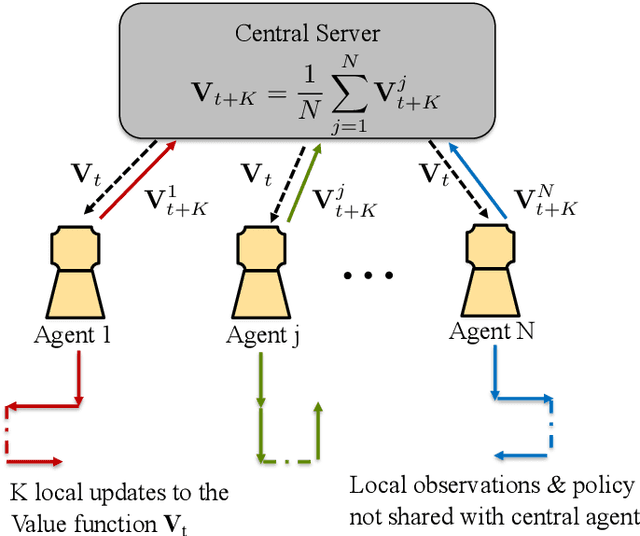
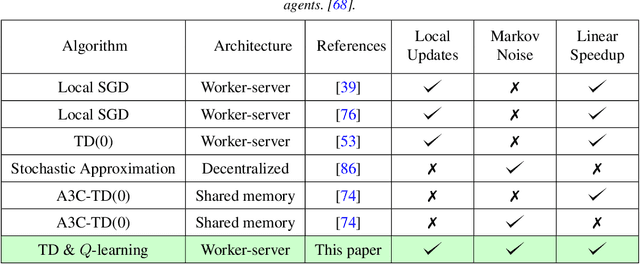
Since reinforcement learning algorithms are notoriously data-intensive, the task of sampling observations from the environment is usually split across multiple agents. However, transferring these observations from the agents to a central location can be prohibitively expensive in terms of the communication cost, and it can also compromise the privacy of each agent's local behavior policy. In this paper, we consider a federated reinforcement learning framework where multiple agents collaboratively learn a global model, without sharing their individual data and policies. Each agent maintains a local copy of the model and updates it using locally sampled data. Although having N agents enables the sampling of N times more data, it is not clear if it leads to proportional convergence speedup. We propose federated versions of on-policy TD, off-policy TD and Q-learning, and analyze their convergence. For all these algorithms, to the best of our knowledge, we are the first to consider Markovian noise and multiple local updates, and prove a linear convergence speedup with respect to the number of agents. To obtain these results, we show that federated TD and Q-learning are special cases of a general framework for federated stochastic approximation with Markovian noise, and we leverage this framework to provide a unified convergence analysis that applies to all the algorithms.

Information Theoretic Measures for Fairness-aware Feature Selection

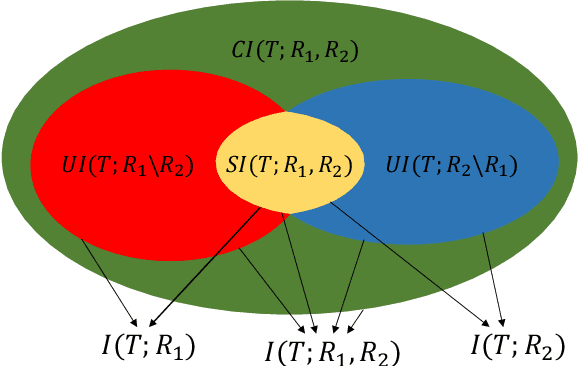
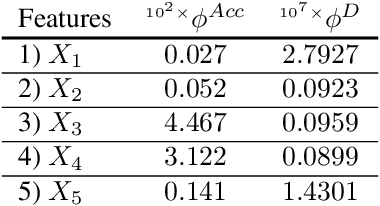
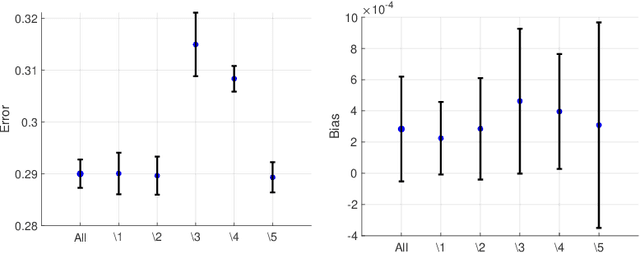
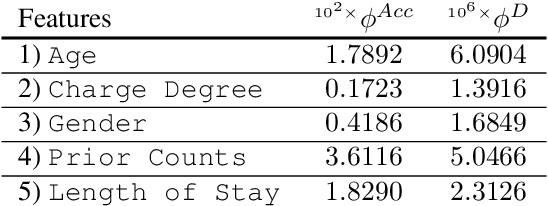
Machine learning algorithms are increasingly used for consequential decision making regarding individuals based on their relevant features. Features that are relevant for accurate decisions may however lead to either explicit or implicit forms of discrimination against unprivileged groups, such as those of certain race or gender. This happens due to existing biases in the training data, which are often replicated or even exacerbated by the learning algorithm. Identifying and measuring these biases at the data level is a challenging problem due to the interdependence among the features, and the decision outcome. In this work, we develop a framework for fairness-aware feature selection which takes into account the correlation among the features and the decision outcome, and is based on information theoretic measures for the accuracy and discriminatory impacts of features. In particular, we first propose information theoretic measures which quantify the impact of different subsets of features on the accuracy and discrimination of the decision outcomes. We then deduce the marginal impact of each feature using Shapley value function; a solution concept in cooperative game theory used to estimate marginal contributions of players in a coalitional game. Finally, we design a fairness utility score for each feature (for feature selection) which quantifies how this feature influences accurate as well as nondiscriminatory decisions. Our framework depends on the joint statistics of the data rather than a particular classifier design. We examine our proposed framework on real and synthetic data to evaluate its performance.

Finite-Sample Analysis of Off-Policy Natural Actor-Critic with Linear Function Approximation

In this paper, we develop a novel variant of off-policy natural actor-critic algorithm with linear function approximation and we establish a sample complexity of $\mathcal{O}(\epsilon^{-3})$, outperforming all the previously known convergence bounds of such algorithms. In order to overcome the divergence due to deadly triad in off-policy policy evaluation under function approximation, we develop a critic that employs $n$-step TD-learning algorithm with a properly chosen $n$. We present finite-sample convergence bounds on this critic under both constant and diminishing step sizes, which are of independent interest. Furthermore, we develop a variant of natural policy gradient under function approximation, with an improved convergence rate of $\mathcal{O}(1/T)$ after $T$ iterations. Combining the finite sample error bounds of actor and the critic, we obtain the $\mathcal{O}(\epsilon^{-3})$ sample complexity. We derive our sample complexity bounds solely based on the assumption that the behavior policy sufficiently explores all the states and actions, which is a much lighter assumption compared to the related literature.

On the Linear convergence of Natural Policy Gradient Algorithm

Markov Decision Processes are classically solved using Value Iteration and Policy Iteration algorithms. Recent interest in Reinforcement Learning has motivated the study of methods inspired by optimization, such as gradient ascent. Among these, a popular algorithm is the Natural Policy Gradient, which is a mirror descent variant for MDPs. This algorithm forms the basis of several popular Reinforcement Learning algorithms such as Natural actor-critic, TRPO, PPO, etc, and so is being studied with growing interest. It has been shown that Natural Policy Gradient with constant step size converges with a sublinear rate of O(1/k) to the global optimal. In this paper, we present improved finite time convergence bounds, and show that this algorithm has geometric (also known as linear) asymptotic convergence rate. We further improve this convergence result by introducing a variant of Natural Policy Gradient with adaptive step sizes. Finally, we compare different variants of policy gradient methods experimentally.

Finite-Sample Analysis of Off-Policy Natural Actor-Critic Algorithm

In this paper, we provide finite-sample convergence guarantees for an off-policy variant of the natural actor-critic (NAC) algorithm based on Importance Sampling. In particular, we show that the algorithm converges to a global optimal policy with a sample complexity of $\mathcal{O}(\epsilon^{-3}\log^2(1/\epsilon))$ under an appropriate choice of stepsizes. In order to overcome the issue of large variance due to Importance Sampling, we propose the $Q$-trace algorithm for the critic, which is inspired by the V-trace algorithm (Espeholt et al., 2018). This enables us to explicitly control the bias and variance, and characterize the trade-off between them. As an advantage of off-policy sampling, a major feature of our result is that we do not need any additional assumptions, beyond the ergodicity of the Markov chain induced by the behavior policy.

Impact of Data Processing on Fairness in Supervised Learning

We study the impact of pre and post processing for reducing discrimination in data-driven decision makers. We first analyze the fundamental trade-off between fairness and accuracy in a pre-processing approach, and propose a design for a pre-processing module based on a convex optimization program, which can be added before the original classifier. This leads to a fundamental lower bound on attainable discrimination, given any acceptable distortion in the outcome. Furthermore, we reformulate an existing post-processing method in terms of our accuracy and fairness measures, which allows comparing post-processing and pre-processing approaches. We show that under some mild conditions, pre-processing outperforms post-processing. Finally, we show that by appropriate choice of the discrimination measure, the optimization problem for both pre and post processing approaches will reduce to a linear program and hence can be solved efficiently.