Centralized and Federated Heart Disease Classification Models Using UCI Dataset and their Shapley-value Based Interpretability

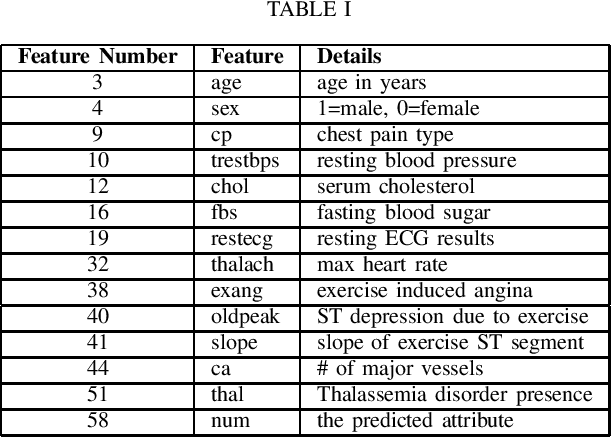
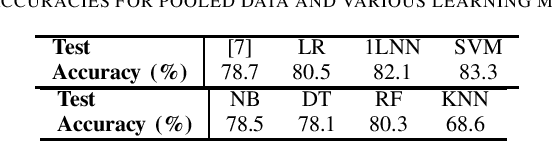
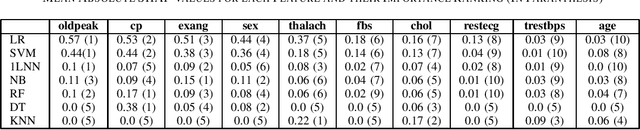
Cardiovascular diseases are a leading cause of mortality worldwide, highlighting the need for accurate diagnostic methods. This study benchmarks centralized and federated machine learning algorithms for heart disease classification using the UCI dataset which includes 920 patient records from four hospitals in the USA, Hungary and Switzerland. Our benchmark is supported by Shapley-value interpretability analysis to quantify features' importance for classification. In the centralized setup, various binary classification algorithms are trained on pooled data, with a support vector machine (SVM) achieving the highest testing accuracy of 83.3\%, surpassing the established benchmark of 78.7\% with logistic regression. Additionally, federated learning algorithms with four clients (hospitals) are explored, leveraging the dataset's natural partition to enhance privacy without sacrificing accuracy. Federated SVM, an uncommon approach in the literature, achieves a top testing accuracy of 73.8\%. Our interpretability analysis aligns with existing medical knowledge of heart disease indicators. Overall, this study establishes a benchmark for efficient and interpretable pre-screening tools for heart disease while maintaining patients' privacy.

Causal Discovery in Linear Models with Unobserved Variables and Measurement Error

The presence of unobserved common causes and the presence of measurement error are two of the most limiting challenges in the task of causal structure learning. Ignoring either of the two challenges can lead to detecting spurious causal links among variables of interest. In this paper, we study the problem of causal discovery in systems where these two challenges can be present simultaneously. We consider linear models which include four types of variables: variables that are directly observed, variables that are not directly observed but are measured with error, the corresponding measurements, and variables that are neither observed nor measured. We characterize the extent of identifiability of such model under separability condition (i.e., the matrix indicating the independent exogenous noise terms pertaining to the observed variables is identifiable) together with two versions of faithfulness assumptions and propose a notion of observational equivalence. We provide graphical characterization of the models that are equivalent and present a recovery algorithm that could return models equivalent to the ground truth.

Causal Discovery in Linear Latent Variable Models Subject to Measurement Error

We focus on causal discovery in the presence of measurement error in linear systems where the mixing matrix, i.e., the matrix indicating the independent exogenous noise terms pertaining to the observed variables, is identified up to permutation and scaling of the columns. We demonstrate a somewhat surprising connection between this problem and causal discovery in the presence of unobserved parentless causes, in the sense that there is a mapping, given by the mixing matrix, between the underlying models to be inferred in these problems. Consequently, any identifiability result based on the mixing matrix for one model translates to an identifiability result for the other model. We characterize to what extent the causal models can be identified under a two-part faithfulness assumption. Under only the first part of the assumption (corresponding to the conventional definition of faithfulness), the structure can be learned up to the causal ordering among an ordered grouping of the variables but not all the edges across the groups can be identified. We further show that if both parts of the faithfulness assumption are imposed, the structure can be learned up to a more refined ordered grouping. As a result of this refinement, for the latent variable model with unobserved parentless causes, the structure can be identified. Based on our theoretical results, we propose causal structure learning methods for both models, and evaluate their performance on synthetic data.

Causal Discovery in Linear Structural Causal Models with Deterministic Relations

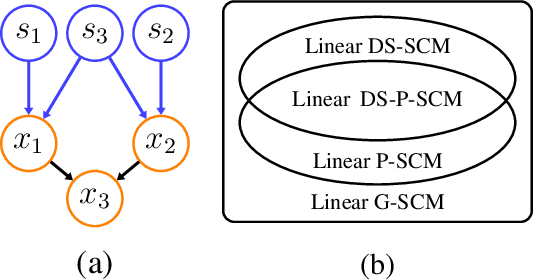
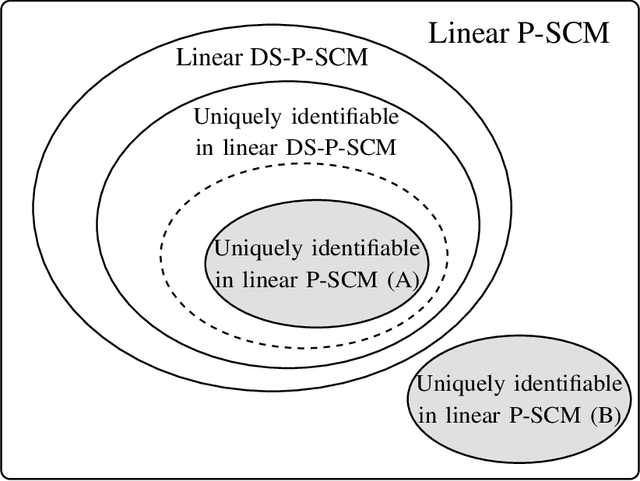
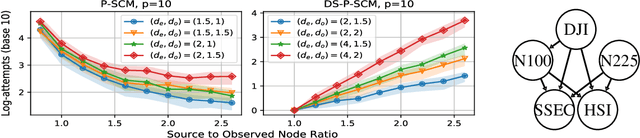
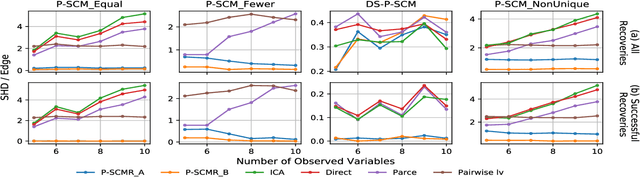
Linear structural causal models (SCMs) -- in which each observed variable is generated by a subset of the other observed variables as well as a subset of the exogenous sources -- are pervasive in causal inference and casual discovery. However, for the task of causal discovery, existing work almost exclusively focus on the submodel where each observed variable is associated with a distinct source with non-zero variance. This results in the restriction that no observed variable can deterministically depend on other observed variables or latent confounders. In this paper, we extend the results on structure learning by focusing on a subclass of linear SCMs which do not have this property, i.e., models in which observed variables can be causally affected by any subset of the sources, and are allowed to be a deterministic function of other observed variables or latent confounders. This allows for a more realistic modeling of influence or information propagation in systems. We focus on the task of causal discovery form observational data generated from a member of this subclass. We derive a set of necessary and sufficient conditions for unique identifiability of the causal structure. To the best of our knowledge, this is the first work that gives identifiability results for causal discovery under both latent confounding and deterministic relationships. Further, we propose an algorithm for recovering the underlying causal structure when the aforementioned conditions are satisfied. We validate our theoretical results both on synthetic and real datasets.

Information Theoretic Measures for Fairness-aware Feature Selection

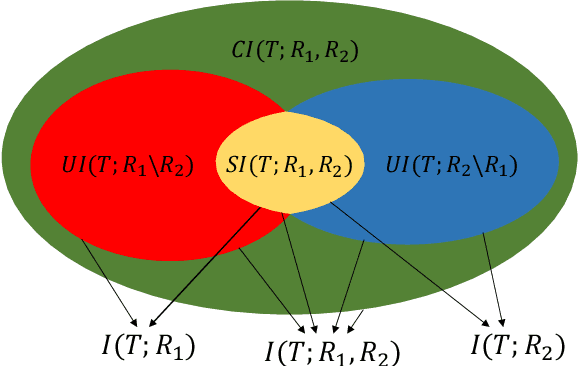
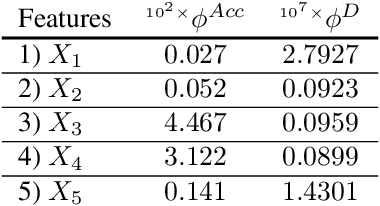
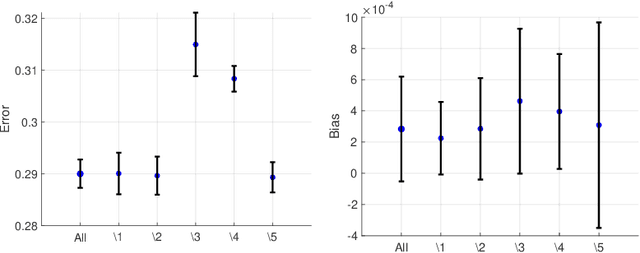
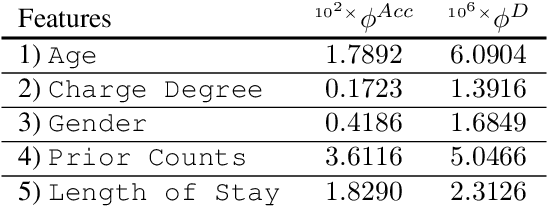
Machine learning algorithms are increasingly used for consequential decision making regarding individuals based on their relevant features. Features that are relevant for accurate decisions may however lead to either explicit or implicit forms of discrimination against unprivileged groups, such as those of certain race or gender. This happens due to existing biases in the training data, which are often replicated or even exacerbated by the learning algorithm. Identifying and measuring these biases at the data level is a challenging problem due to the interdependence among the features, and the decision outcome. In this work, we develop a framework for fairness-aware feature selection which takes into account the correlation among the features and the decision outcome, and is based on information theoretic measures for the accuracy and discriminatory impacts of features. In particular, we first propose information theoretic measures which quantify the impact of different subsets of features on the accuracy and discrimination of the decision outcomes. We then deduce the marginal impact of each feature using Shapley value function; a solution concept in cooperative game theory used to estimate marginal contributions of players in a coalitional game. Finally, we design a fairness utility score for each feature (for feature selection) which quantifies how this feature influences accurate as well as nondiscriminatory decisions. Our framework depends on the joint statistics of the data rather than a particular classifier design. We examine our proposed framework on real and synthetic data to evaluate its performance.