ChatRex: Taming Multimodal LLM for Joint Perception and Understanding

Perception and understanding are two pillars of computer vision. While multimodal large language models (MLLM) have demonstrated remarkable visual understanding capabilities, they arguably lack accurate perception abilities, e.g. the stage-of-the-art model Qwen2-VL only achieves a 43.9 recall rate on the COCO dataset, limiting many tasks requiring the combination of perception and understanding. In this work, we aim to bridge this perception gap from both model designing and data development perspectives. We first introduce ChatRex, an MLLM with a decoupled perception design. Instead of having the LLM directly predict box coordinates, we feed the output boxes from a universal proposal network into the LLM, allowing it to output the corresponding box indices to represent its detection results, turning the regression task into a retrieval-based task that LLM handles more proficiently. From the data perspective, we build a fully automated data engine and construct the Rexverse-2M dataset which possesses multiple granularities to support the joint training of perception and understanding. After standard two-stage training, ChatRex demonstrates strong perception capabilities while preserving multimodal understanding performance. The combination of these two capabilities simultaneously unlocks many attractive applications, demonstrating the complementary roles of both perception and understanding in MLLM. Code is available at \url{https://github.com/IDEA-Research/ChatRex}.

Causal Discovery in Linear Models with Unobserved Variables and Measurement Error

The presence of unobserved common causes and the presence of measurement error are two of the most limiting challenges in the task of causal structure learning. Ignoring either of the two challenges can lead to detecting spurious causal links among variables of interest. In this paper, we study the problem of causal discovery in systems where these two challenges can be present simultaneously. We consider linear models which include four types of variables: variables that are directly observed, variables that are not directly observed but are measured with error, the corresponding measurements, and variables that are neither observed nor measured. We characterize the extent of identifiability of such model under separability condition (i.e., the matrix indicating the independent exogenous noise terms pertaining to the observed variables is identifiable) together with two versions of faithfulness assumptions and propose a notion of observational equivalence. We provide graphical characterization of the models that are equivalent and present a recovery algorithm that could return models equivalent to the ground truth.

Learning Unknown Intervention Targets in Structural Causal Models from Heterogeneous Data

We study the problem of identifying the unknown intervention targets in structural causal models where we have access to heterogeneous data collected from multiple environments. The unknown intervention targets are the set of endogenous variables whose corresponding exogenous noises change across the environments. We propose a two-phase approach which in the first phase recovers the exogenous noises corresponding to unknown intervention targets whose distributions have changed across environments. In the second phase, the recovered noises are matched with the corresponding endogenous variables. For the recovery phase, we provide sufficient conditions for learning these exogenous noises up to some component-wise invertible transformation. For the matching phase, under the causal sufficiency assumption, we show that the proposed method uniquely identifies the intervention targets. In the presence of latent confounders, the intervention targets among the observed variables cannot be determined uniquely. We provide a candidate intervention target set which is a superset of the true intervention targets. Our approach improves upon the state of the art as the returned candidate set is always a subset of the target set returned by previous work. Moreover, we do not require restrictive assumptions such as linearity of the causal model or performing invariance tests to learn whether a distribution is changing across environments which could be highly sample inefficient. Our experimental results show the effectiveness of our proposed algorithm in practice.

Causal Discovery in Linear Latent Variable Models Subject to Measurement Error

We focus on causal discovery in the presence of measurement error in linear systems where the mixing matrix, i.e., the matrix indicating the independent exogenous noise terms pertaining to the observed variables, is identified up to permutation and scaling of the columns. We demonstrate a somewhat surprising connection between this problem and causal discovery in the presence of unobserved parentless causes, in the sense that there is a mapping, given by the mixing matrix, between the underlying models to be inferred in these problems. Consequently, any identifiability result based on the mixing matrix for one model translates to an identifiability result for the other model. We characterize to what extent the causal models can be identified under a two-part faithfulness assumption. Under only the first part of the assumption (corresponding to the conventional definition of faithfulness), the structure can be learned up to the causal ordering among an ordered grouping of the variables but not all the edges across the groups can be identified. We further show that if both parts of the faithfulness assumption are imposed, the structure can be learned up to a more refined ordered grouping. As a result of this refinement, for the latent variable model with unobserved parentless causes, the structure can be identified. Based on our theoretical results, we propose causal structure learning methods for both models, and evaluate their performance on synthetic data.

Causal Discovery in Linear Structural Causal Models with Deterministic Relations

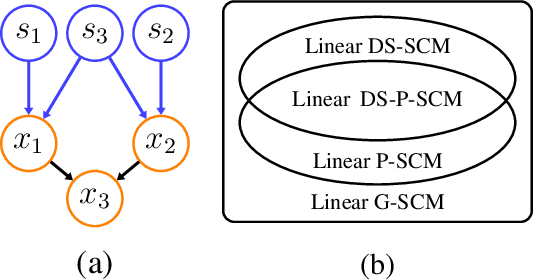
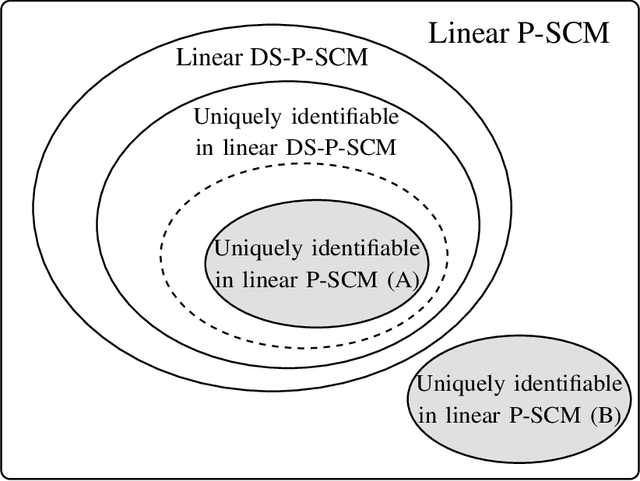
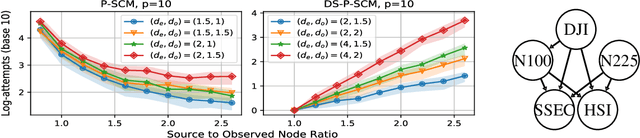
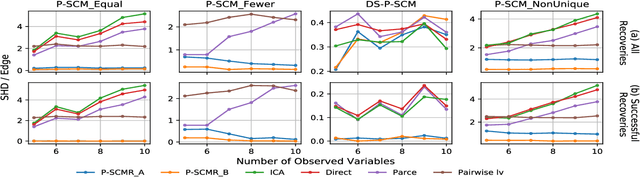
Linear structural causal models (SCMs) -- in which each observed variable is generated by a subset of the other observed variables as well as a subset of the exogenous sources -- are pervasive in causal inference and casual discovery. However, for the task of causal discovery, existing work almost exclusively focus on the submodel where each observed variable is associated with a distinct source with non-zero variance. This results in the restriction that no observed variable can deterministically depend on other observed variables or latent confounders. In this paper, we extend the results on structure learning by focusing on a subclass of linear SCMs which do not have this property, i.e., models in which observed variables can be causally affected by any subset of the sources, and are allowed to be a deterministic function of other observed variables or latent confounders. This allows for a more realistic modeling of influence or information propagation in systems. We focus on the task of causal discovery form observational data generated from a member of this subclass. We derive a set of necessary and sufficient conditions for unique identifiability of the causal structure. To the best of our knowledge, this is the first work that gives identifiability results for causal discovery under both latent confounding and deterministic relationships. Further, we propose an algorithm for recovering the underlying causal structure when the aforementioned conditions are satisfied. We validate our theoretical results both on synthetic and real datasets.