Federated Reinforcement Learning: Linear Speedup Under Markovian Sampling
Paper and Code
Jun 21, 2022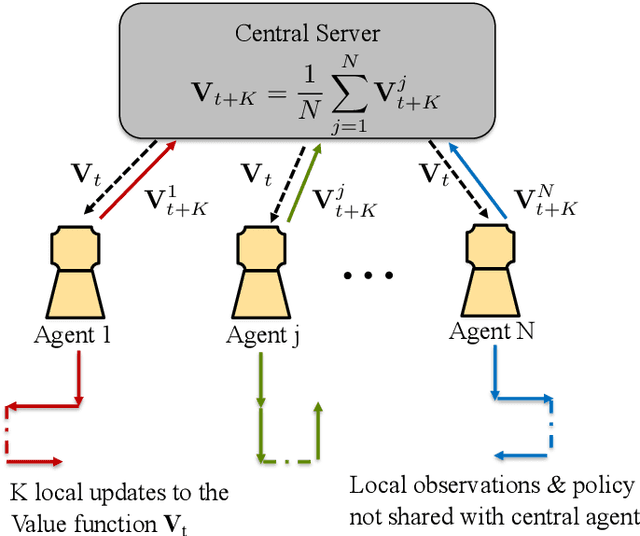
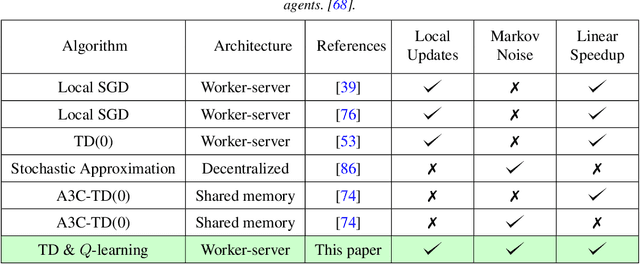
Since reinforcement learning algorithms are notoriously data-intensive, the task of sampling observations from the environment is usually split across multiple agents. However, transferring these observations from the agents to a central location can be prohibitively expensive in terms of the communication cost, and it can also compromise the privacy of each agent's local behavior policy. In this paper, we consider a federated reinforcement learning framework where multiple agents collaboratively learn a global model, without sharing their individual data and policies. Each agent maintains a local copy of the model and updates it using locally sampled data. Although having N agents enables the sampling of N times more data, it is not clear if it leads to proportional convergence speedup. We propose federated versions of on-policy TD, off-policy TD and Q-learning, and analyze their convergence. For all these algorithms, to the best of our knowledge, we are the first to consider Markovian noise and multiple local updates, and prove a linear convergence speedup with respect to the number of agents. To obtain these results, we show that federated TD and Q-learning are special cases of a general framework for federated stochastic approximation with Markovian noise, and we leverage this framework to provide a unified convergence analysis that applies to all the algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge