Online Reinforcement Learning of Optimal Threshold Policies for Markov Decision Processes

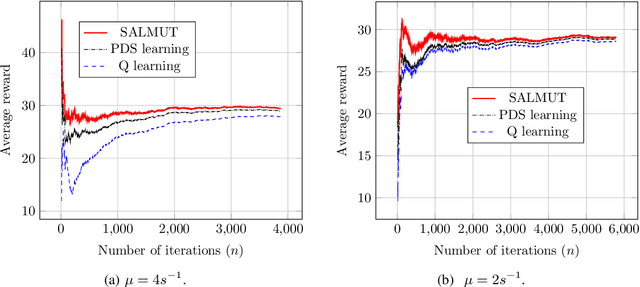
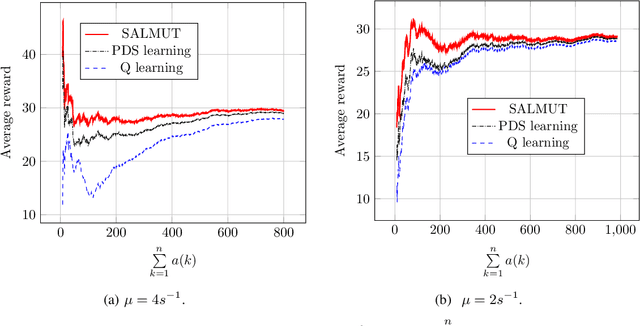
Markov Decision Process (MDP) problems can be solved using Dynamic Programming (DP) methods which suffer from the curse of dimensionality and the curse of modeling. To overcome these issues, Reinforcement Learning (RL) methods are adopted in practice. In this paper, we aim to obtain the optimal admission control policy in a system where different classes of customers are present. Using DP techniques, we prove that it is optimal to admit the $i$ th class of customers only upto a threshold $\tau(i)$ which is a non-increasing function of $i$. Contrary to traditional RL algorithms which do not take into account the structural properties of the optimal policy while learning, we propose a structure-aware learning algorithm which exploits the threshold structure of the optimal policy. We prove the asymptotic convergence of the proposed algorithm to the optimal policy. Due to the reduction in the policy space, the structure-aware learning algorithm provides remarkable improvements in storage and computational complexities over classical RL algorithms. Simulation results also establish the gain in the convergence rate of the proposed algorithm over other RL algorithms. The techniques presented in the paper can be applied to any general MDP problem covering various applications such as inventory management, financial planning and communication networking.

A Structure-aware Online Learning Algorithm for Markov Decision Processes

To overcome the curse of dimensionality and curse of modeling in Dynamic Programming (DP) methods for solving classical Markov Decision Process (MDP) problems, Reinforcement Learning (RL) algorithms are popular. In this paper, we consider an infinite-horizon average reward MDP problem and prove the optimality of the threshold policy under certain conditions. Traditional RL techniques do not exploit the threshold nature of optimal policy while learning. In this paper, we propose a new RL algorithm which utilizes the known threshold structure of the optimal policy while learning by reducing the feasible policy space. We establish that the proposed algorithm converges to the optimal policy. It provides a significant improvement in convergence speed and computational and storage complexity over traditional RL algorithms. The proposed technique can be applied to a wide variety of optimization problems that include energy efficient data transmission and management of queues. We exhibit the improvement in convergence speed of the proposed algorithm over other RL algorithms through simulations.

Rate Constrained Random Access over a Fading Channel

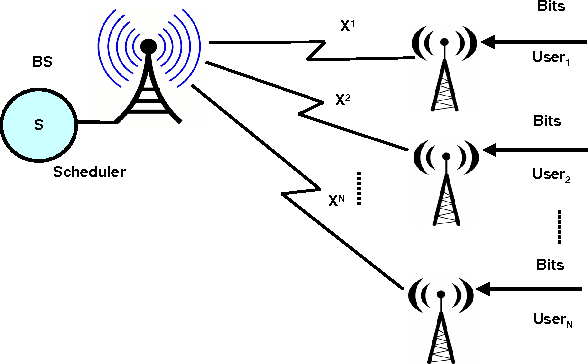
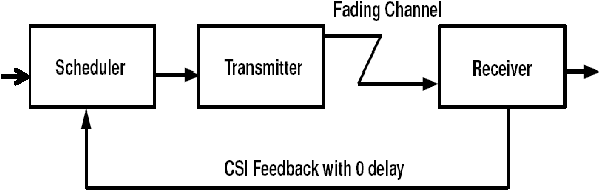
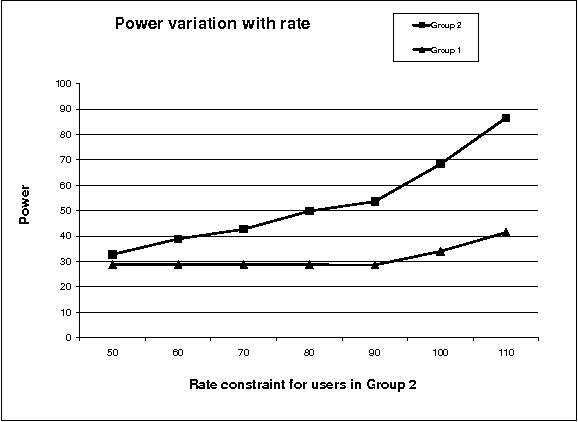
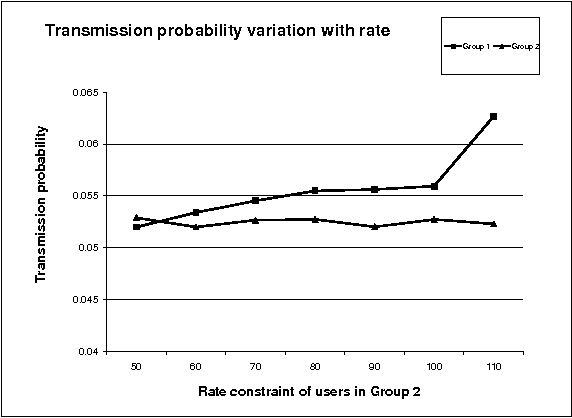
In this paper, we consider uplink transmissions involving multiple users communicating with a base station over a fading channel. We assume that the base station does not coordinate the transmissions of the users and hence the users employ random access communication. The situation is modeled as a non-cooperative repeated game with incomplete information. Each user attempts to minimize its long term power consumption subject to a minimum rate requirement. We propose a two timescale stochastic gradient algorithm (TTSGA) for tuning the users' transmission probabilities. The algorithm includes a 'waterfilling threshold update mechanism' that ensures that the rate constraints are satisfied. We prove that under the algorithm, the users' transmission probabilities converge to a Nash equilibrium. Moreover, we also prove that the rate constraints are satisfied; this is also demonstrated using simulation studies.