Nitin Salodkar
Rate Constrained Random Access over a Fading Channel
Aug 22, 2009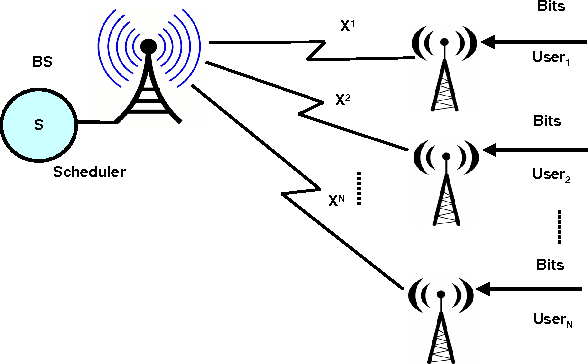
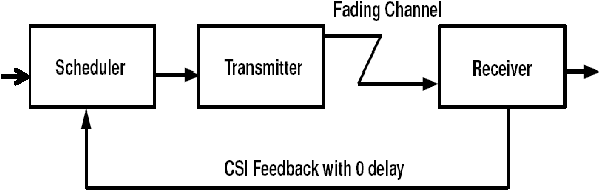
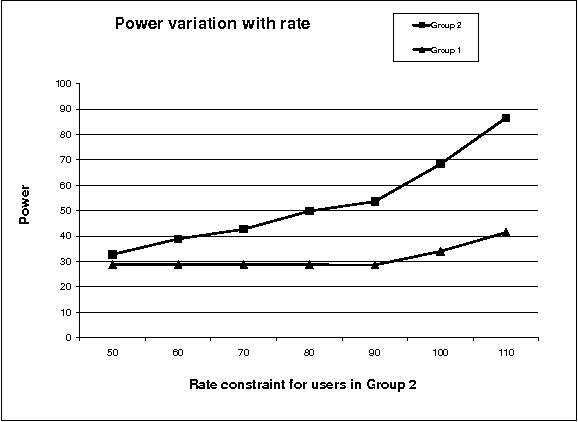
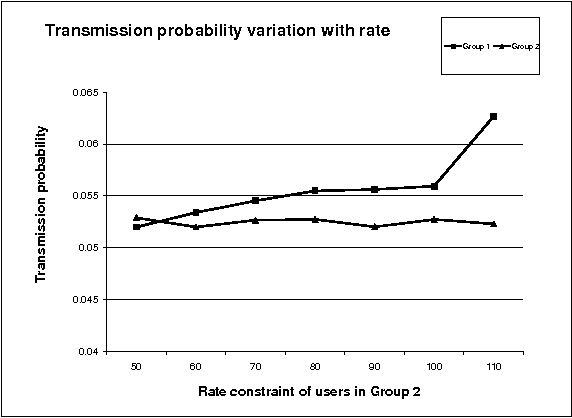
Abstract:In this paper, we consider uplink transmissions involving multiple users communicating with a base station over a fading channel. We assume that the base station does not coordinate the transmissions of the users and hence the users employ random access communication. The situation is modeled as a non-cooperative repeated game with incomplete information. Each user attempts to minimize its long term power consumption subject to a minimum rate requirement. We propose a two timescale stochastic gradient algorithm (TTSGA) for tuning the users' transmission probabilities. The algorithm includes a 'waterfilling threshold update mechanism' that ensures that the rate constraints are satisfied. We prove that under the algorithm, the users' transmission probabilities converge to a Nash equilibrium. Moreover, we also prove that the rate constraints are satisfied; this is also demonstrated using simulation studies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge