A network community detection method with integration of data from multiple layers and node attributes

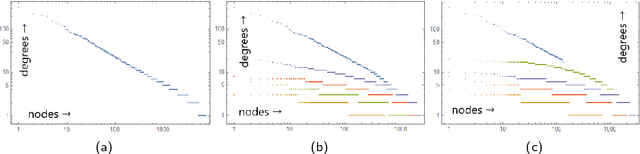
Multilayer networks are in the focus of the current complex network study. In such networks multiple types of links may exist as well as many attributes for nodes. To fully use multilayer -- and other types of complex networks in applications, the merging of various data with topological information renders a powerful analysis. First, we suggest a simple way of representing network data in a data matrix where rows correspond to the nodes, and columns correspond to the data items. The number of columns is allowed to be arbitrary, so that the data matrix can be easily expanded by adding columns. The data matrix can be chosen according to targets of the analysis, and may vary a lot from case to case. Next, we partition the rows of the data matrix into communities using a method which allows maximal compression of the data matrix. For compressing a data matrix, we suggest to extend so called regular decomposition method for non-square matrices. We illustrate our method for several types of data matrices, in particular, distance matrices, and matrices obtained by augmenting a distance matrix by a column of node degrees, or by concatenating several distances matrices corresponding to layers of a multilayer network. We illustrate our method with synthetic power-law graphs and two real networks: an Internet autonomous systems graph and a world airline graph. We compare the outputs of different community recovery methods on these graphs, and discuss how incorporating node degrees as a separate column to the data matrix leads our method to identify community structures well-aligned with tiered hierarchical structures commonly encountered in complex scale-free networks.

Multilayer hypergraph clustering using the aggregate similarity matrix

We consider the community recovery problem on a multilayer variant of the hypergraph stochastic block model (HSBM). Each layer is associated with an independent realization of a d-uniform HSBM on N vertices. Given the aggregated number of hyperedges incident to each pair of vertices, represented using a similarity matrix, the goal is to obtain a partition of the N vertices into disjoint communities. In this work, we investigate a semidefinite programming (SDP) approach and obtain information-theoretic conditions on the model parameters that guarantee exact recovery both in the assortative and the disassortative cases.

Estimation of Static Community Memberships from Temporal Network Data

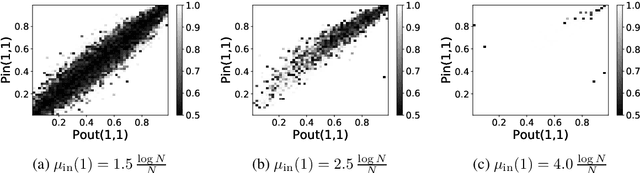
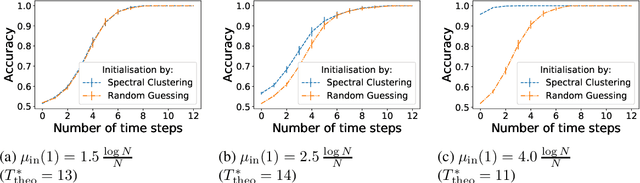
This article studies the estimation of static community memberships from temporally correlated pair interactions represented by an $N$-by-$N$-by-$T$ tensor where $N$ is the number of nodes and $T$ is the length of the time horizon. We present several estimation algorithms, both offline and online, which fully utilise the temporal nature of the observed data. As an information-theoretic benchmark, we study data sets generated by a dynamic stochastic block model, and derive fundamental information criteria for the recoverability of the community memberships as $N \to \infty$ both for bounded and diverging $T$. These results show that (i) even a small increase in $T$ may have a big impact on the recoverability of community memberships, (ii) consistent recovery is possible even for very sparse data (e.g. bounded average degree) when $T$ is large enough. We analyse the accuracy of the proposed estimation algorithms under various assumptions on data sparsity and identifiability, and prove that an efficient online algorithm is strongly consistent up to the information-theoretic threshold under suitable initialisation. Numerical experiments show that even a poor initial estimate (e.g., blind random guess) of the community assignment leads to high accuracy after a small number of iterations, and remarkably so also in very sparse regimes.

Towards analyzing large graphs with quantum annealing and quantum gate computers

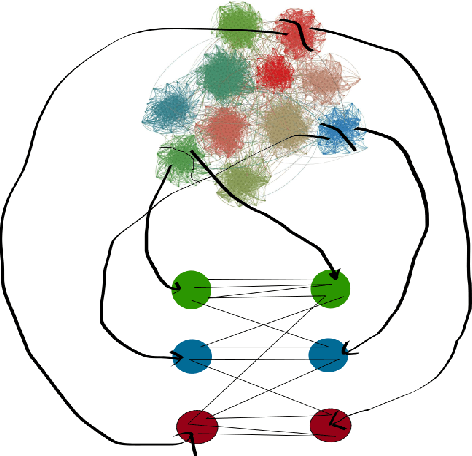
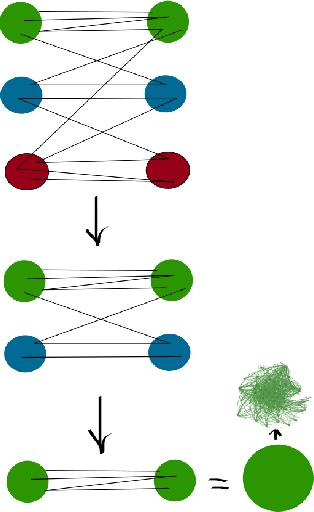
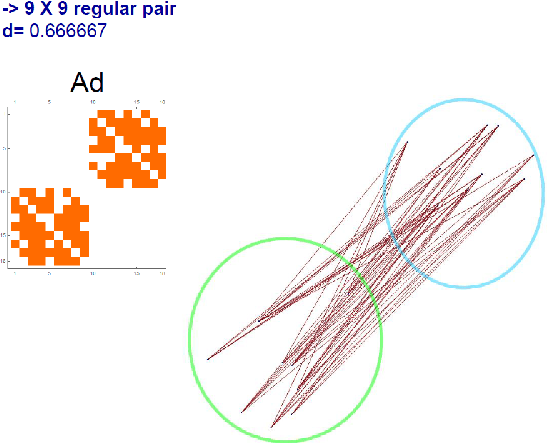
The use of quantum computing in graph community detection and regularity checking related to Szemeredi's Regularity Lemma (SRL) are demonstrated with D-Wave Systems' quantum annealer and simulations. We demonstrate the capability of quantum computing in solving hard problems relevant to big data. A new community detection algorithm based on SRL is also introduced and tested. In worst case scenario of regularity check we use Grover's algorithm and quantum phase estimation algorithm, in order to speed-up computations using a quantum gate computers.