Recycling History: Efficient Recommendations from Contextual Dueling Bandits

The contextual duelling bandit problem models adaptive recommender systems, where the algorithm presents a set of items to the user, and the user's choice reveals their preference. This setup is well suited for implicit choices users make when navigating a content platform, but does not capture other possible comparison queries. Motivated by the fact that users provide more reliable feedback after consuming items, we propose a new bandit model that can be described as follows. The algorithm recommends one item per time step; after consuming that item, the user is asked to compare it with another item chosen from the user's consumption history. Importantly, in our model, this comparison item can be chosen without incurring any additional regret, potentially leading to better performance. However, the regret analysis is challenging because of the temporal dependency in the user's history. To overcome this challenge, we first show that the algorithm can construct informative queries provided the history is rich, i.e., satisfies a certain diversity condition. We then show that a short initial random exploration phase is sufficient for the algorithm to accumulate a rich history with high probability. This result, proven via matrix concentration bounds, yields $O(\sqrt{T})$ regret guarantees. Additionally, our simulations show that reusing past items for comparisons can lead to significantly lower regret than only comparing between simultaneously recommended items.

Measuring IIA Violations in Similarity Choices with Bayesian Models

Similarity choice data occur when humans make choices among alternatives based on their similarity to a target, e.g., in the context of information retrieval and in embedding learning settings. Classical metric-based models of similarity choice assume independence of irrelevant alternatives (IIA), a property that allows for a simpler formulation. While IIA violations have been detected in many discrete choice settings, the similarity choice setting has received scant attention. This is because the target-dependent nature of the choice complicates IIA testing. We propose two statistical methods to test for IIA: a classical goodness-of-fit test and a Bayesian counterpart based on the framework of Posterior Predictive Checks (PPC). This Bayesian approach, our main technical contribution, quantifies the degree of IIA violation beyond its mere significance. We curate two datasets: one with choice sets designed to elicit IIA violations, and another with randomly generated choice sets from the same item universe. Our tests confirmed significant IIA violations on both datasets, and notably, we find a comparable degree of violation between them. Further, we devise a new PPC test for population homogeneity. Results show that the population is indeed homogenous, suggesting that the IIA violations are driven by context effects -- specifically, interactions within the choice sets. These results highlight the need for new similarity choice models that account for such context effects.

Recommendations from Sparse Comparison Data: Provably Fast Convergence for Nonconvex Matrix Factorization

This paper provides a theoretical analysis of a new learning problem for recommender systems where users provide feedback by comparing pairs of items instead of rating them individually. We assume that comparisons stem from latent user and item features, which reduces the task of predicting preferences to learning these features from comparison data. Similar to the classical matrix factorization problem, the main challenge in this learning task is that the resulting loss function is nonconvex. Our analysis shows that the loss function exhibits (restricted) strong convexity near the true solution, which ensures gradient-based methods converge exponentially, given an appropriate warm start. Importantly, this result holds in a sparse data regime, where each user compares only a few pairs of items. Our main technical contribution is to extend certain concentration inequalities commonly used in matrix completion to our model. Our work demonstrates that learning personalized recommendations from comparison data is computationally and statistically efficient.

Community Recovery in a Preferential Attachment Graph

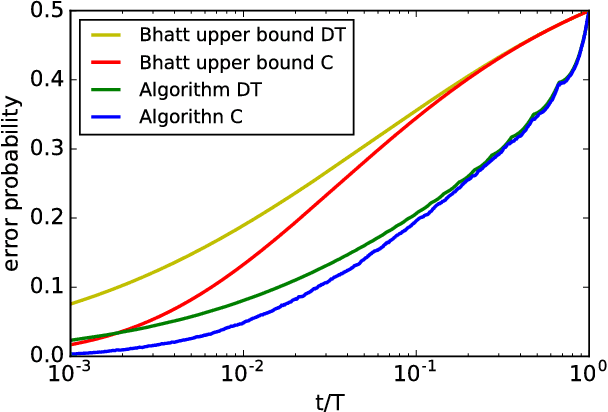
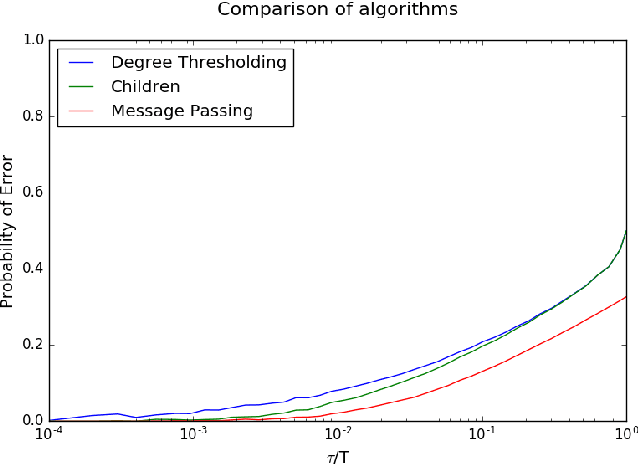
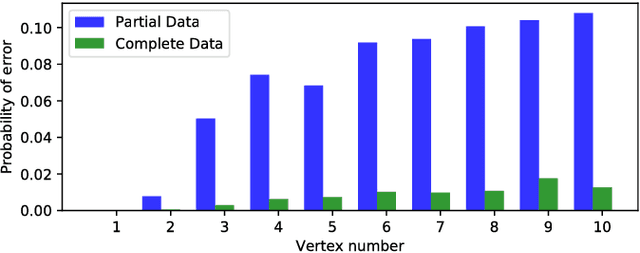
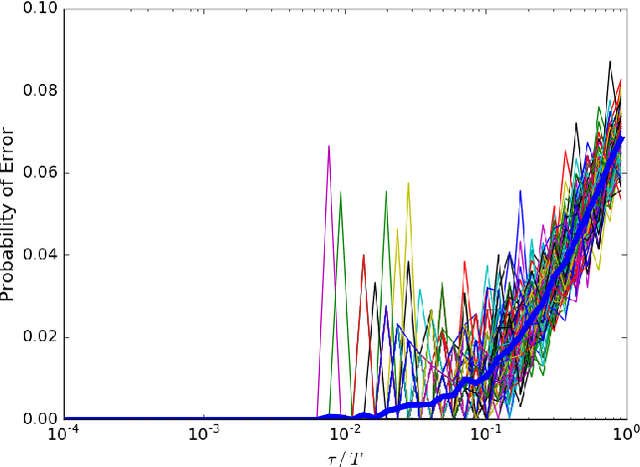
A message passing algorithm is derived for recovering communities within a graph generated by a variation of the Barab\'{a}si-Albert preferential attachment model. The estimator is assumed to know the arrival times, or order of attachment, of the vertices. The derivation of the algorithm is based on belief propagation under an independence assumption. Two precursors to the message passing algorithm are analyzed: the first is a degree thresholding (DT) algorithm and the second is an algorithm based on the arrival times of the children (C) of a given vertex, where the children of a given vertex are the vertices that attached to it. Comparison of the performance of the algorithms shows it is beneficial to know the arrival times, not just the number, of the children. The probability of correct classification of a vertex is asymptotically determined by the fraction of vertices arriving before it. Two extensions of Algorithm C are given: the first is based on joint likelihood of the children of a fixed set of vertices; it can sometimes be used to seed the message passing algorithm. The second is the message passing algorithm. Simulation results are given.

Preferential Attachment Graphs with Planted Communities

A variation of the preferential attachment random graph model of Barab\'asi and Albert is defined that incorporates planted communities. The graph is built progressively, with new vertices attaching to the existing ones one-by-one. At every step, the incoming vertex is randomly assigned a label, which represents a community it belongs to. This vertex then chooses certain vertices as its neighbors, with the choice of each vertex being proportional to the degree of the vertex multiplied by an affinity depending on the labels of the new vertex and a potential neighbor. It is shown that the fraction of half-edges attached to vertices with a given label converges almost surely for some classes of affinity matrices. In addition, the empirical degree distribution for the set of vertices with a given label converges to a heavy tailed distribution, such that the tail decay parameter can be different for different communities. Our proof method may be of independent interest, both for the classical Barab\'asi -Albert model and for other possible extensions.