Get our free extension to see links to code for papers anywhere online!

Chrome logo Add to Chrome

Firefox logo Add to Firefox
Picture for Bruce Hajek

Bruce Hajek

Regenerative Particle Thompson Sampling


Mar 15, 2022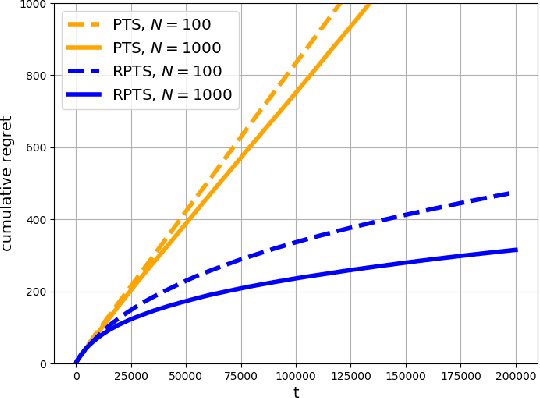
Zeyu Zhou, Bruce Hajek, Nakjung Choi, Anwar Walid

Figure 1 for Regenerative Particle Thompson Sampling
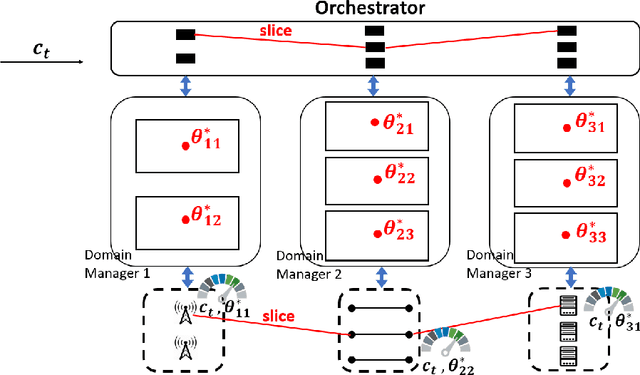
Figure 2 for Regenerative Particle Thompson Sampling
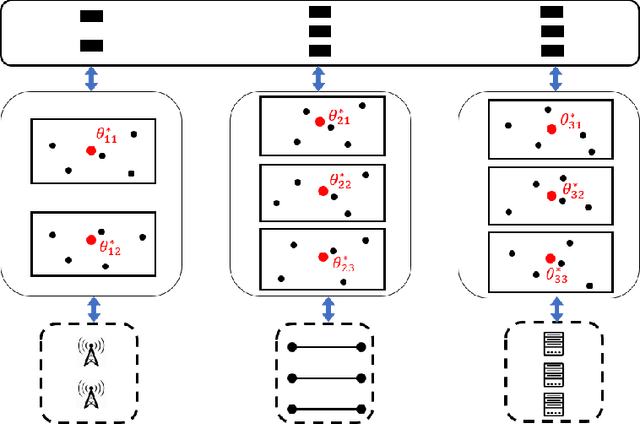
Figure 3 for Regenerative Particle Thompson Sampling
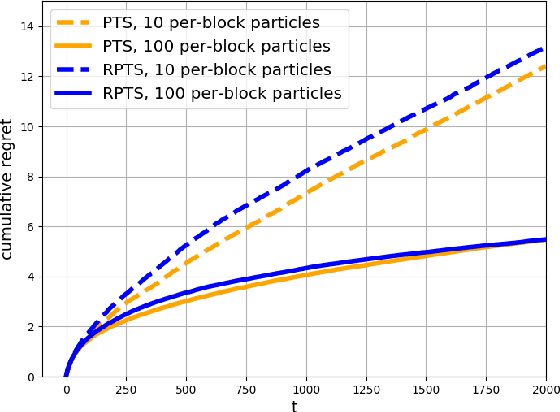
Figure 4 for Regenerative Particle Thompson Sampling
* Mainbody 14 pages, appendix 32 pages, 16 figures 
  Access Paper or Ask Questions

Community Recovery in a Preferential Attachment Graph


Jul 20, 2018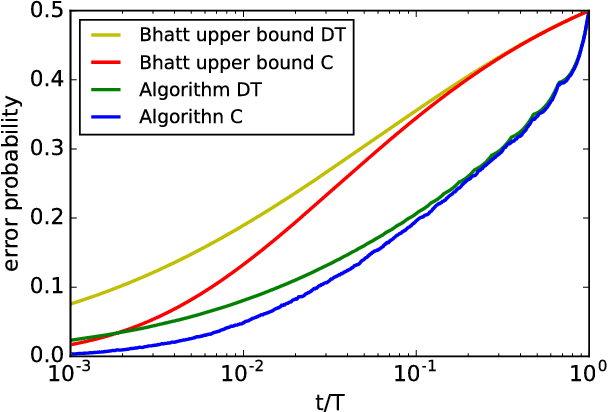
Bruce Hajek, Suryanarayana Sankagiri

Figure 1 for Community Recovery in a Preferential Attachment Graph
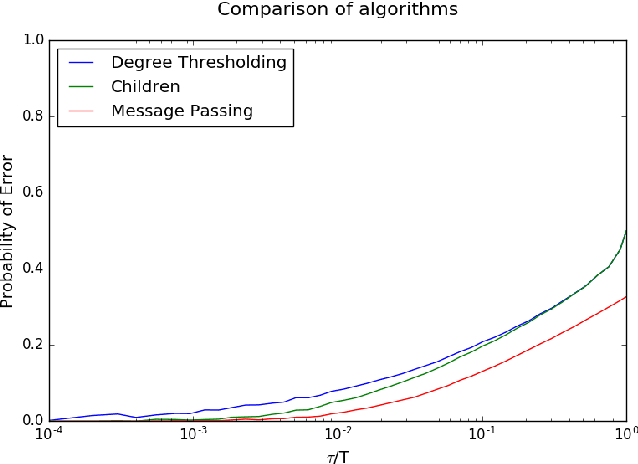
Figure 2 for Community Recovery in a Preferential Attachment Graph
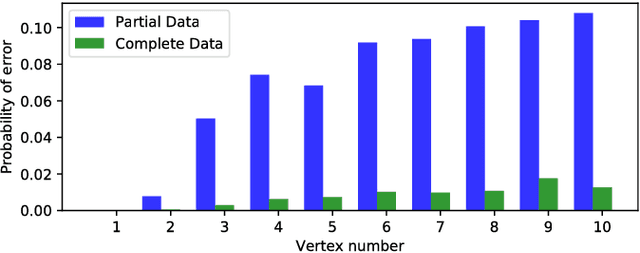
Figure 3 for Community Recovery in a Preferential Attachment Graph
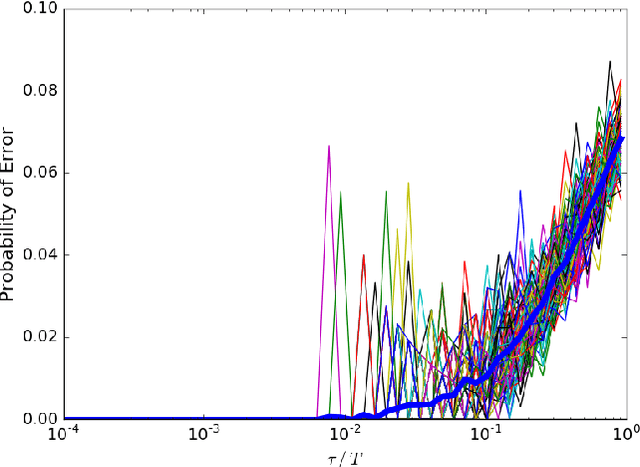
Figure 4 for Community Recovery in a Preferential Attachment Graph
* arXiv admin note: text overlap with arXiv:1801.06816 
  Access Paper or Ask Questions

Preferential Attachment Graphs with Planted Communities


Jan 27, 2018
Bruce Hajek, Suryanarayana Sankagiri

* Discovered large overlap with J. Jordan, Geometric preferential attachment in non-uniform metric spaces (2013) Electronic J. Prob, Vol. 18, no. 8, pp 1-15. New aspects of our approach will be moved to: Recovering a Hidden Community in a Preferential Attachment Graph, arXiv:1801.06818 
  Access Paper or Ask Questions

Recovering a Hidden Community Beyond the Kesten-Stigum Threshold in $O(|E| \log^*|V|)$ Time


Jan 16, 2018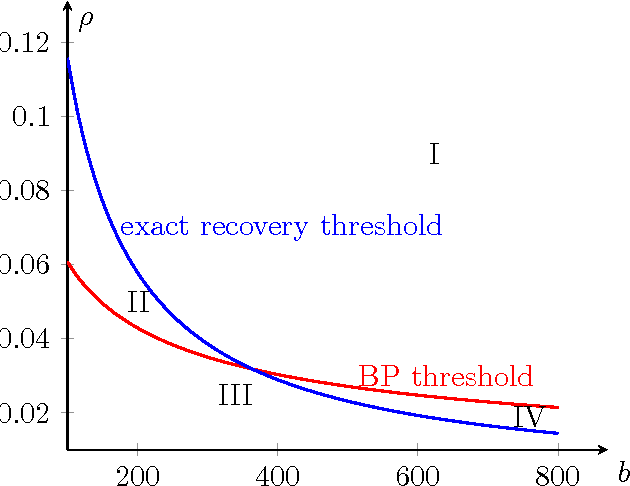
Bruce Hajek, Yihong Wu, Jiaming Xu

Figure 1 for Recovering a Hidden Community Beyond the Kesten-Stigum Threshold in $O(|E| \log^*|V|)$ Time
* New title replaces spectral limit by Kesten-Stigum threshold 
  Access Paper or Ask Questions

Achieving Exact Cluster Recovery Threshold via Semidefinite Programming: Extensions


Jun 15, 2016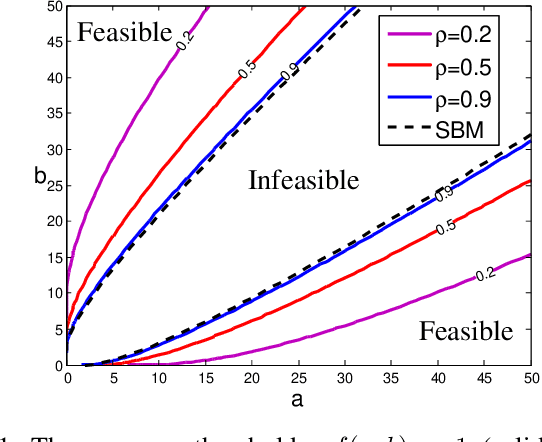
Bruce Hajek, Yihong Wu, Jiaming Xu

Figure 1 for Achieving Exact Cluster Recovery Threshold via Semidefinite Programming: Extensions
* This paper was accepted to IEEE Transactions on Information Theory on April 25, 2016. The material was presented in part at the 2015 49th Asilomar Conference on Signals, Systems and Computers and the 2015 IEEE Information Theory Workshop. This work was also in part presented at the Workshop on Community Detection, February 26-27, Institut Henri Poincar\'e, Paris 
  Access Paper or Ask Questions

Semidefinite Programs for Exact Recovery of a Hidden Community


Jun 03, 2016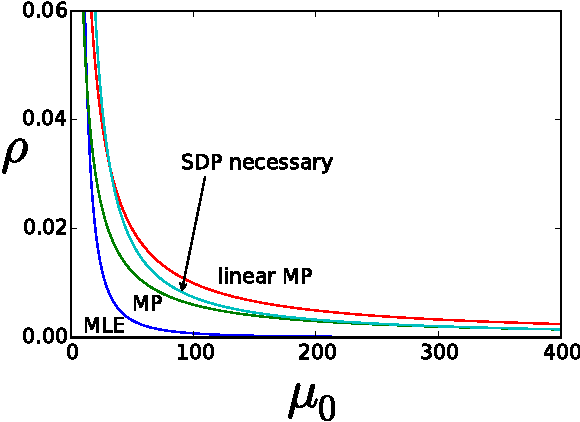
Bruce Hajek, Yihong Wu, Jiaming Xu

Figure 1 for Semidefinite Programs for Exact Recovery of a Hidden Community

  Access Paper or Ask Questions

Information Limits for Recovering a Hidden Community


Jan 25, 2016
Bruce Hajek, Yihong Wu, Jiaming Xu

* v2 establishes information limits of both weak and exact recovery with sharp constants for general P and Q 
  Access Paper or Ask Questions

Achieving Exact Cluster Recovery Threshold via Semidefinite Programming


Jan 05, 2016
Bruce Hajek, Yihong Wu, Jiaming Xu

Figure 1 for Achieving Exact Cluster Recovery Threshold via Semidefinite Programming
* This paper was accepted to IEEE Transactions on Information Theory on January 3, 2016 
  Access Paper or Ask Questions

Clustering and Inference From Pairwise Comparisons


Dec 17, 2015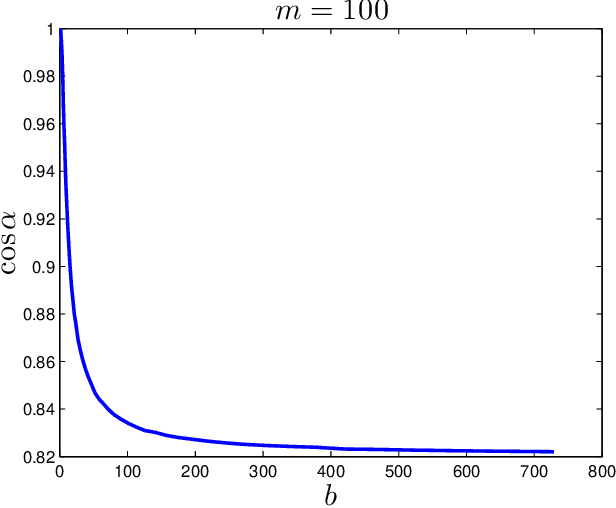
Rui Wu, Jiaming Xu, R. Srikant, Laurent Massoulié, Marc Lelarge, Bruce Hajek

Figure 1 for Clustering and Inference From Pairwise Comparisons
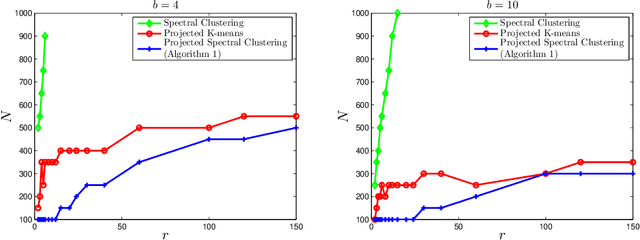
Figure 2 for Clustering and Inference From Pairwise Comparisons
Figure 3 for Clustering and Inference From Pairwise Comparisons
* Corrected typos in the abstract 
  Access Paper or Ask Questions

Submatrix localization via message passing


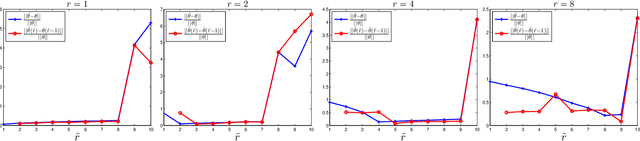
Oct 30, 2015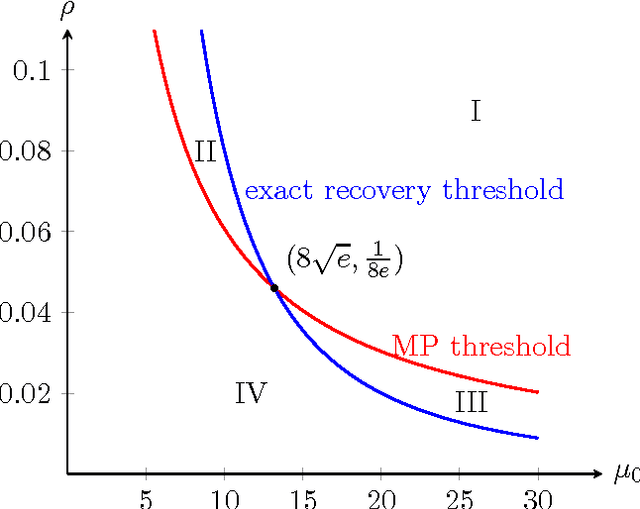
Bruce Hajek, Yihong Wu, Jiaming Xu

Figure 1 for Submatrix localization via message passing
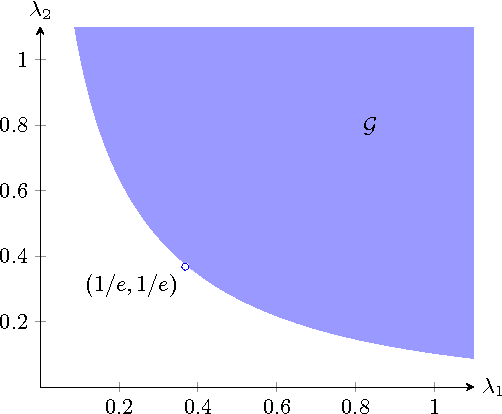
Figure 2 for Submatrix localization via message passing
Figure 3 for Submatrix localization via message passing

  Access Paper or Ask Questions

Computational Lower Bounds for Community Detection on Random Graphs


Mar 11, 2015
Bruce Hajek, Yihong Wu, Jiaming Xu

* 28 pages 
  Access Paper or Ask Questions

Minimax-optimal Inference from Partial Rankings


Jun 21, 2014
Bruce Hajek, Sewoong Oh, Jiaming Xu

Figure 1 for Minimax-optimal Inference from Partial Rankings
* 16 pages, 2 figures 
  Access Paper or Ask Questions

Jointly Clustering Rows and Columns of Binary Matrices: Algorithms and Trade-offs


Feb 04, 2014
Jiaming Xu, Rui Wu, Kai Zhu, Bruce Hajek, R. Srikant, Lei Ying

Figure 1 for Jointly Clustering Rows and Columns of Binary Matrices: Algorithms and Trade-offs
Figure 2 for Jointly Clustering Rows and Columns of Binary Matrices: Algorithms and Trade-offs
Figure 3 for Jointly Clustering Rows and Columns of Binary Matrices: Algorithms and Trade-offs
Figure 4 for Jointly Clustering Rows and Columns of Binary Matrices: Algorithms and Trade-offs

  Access Paper or Ask Questions