Semidefinite Programs for Exact Recovery of a Hidden Community
Paper and Code
Jun 03, 2016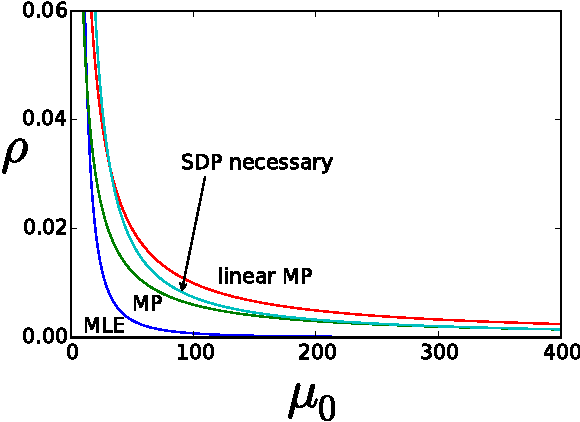
We study a semidefinite programming (SDP) relaxation of the maximum likelihood estimation for exactly recovering a hidden community of cardinality $K$ from an $n \times n$ symmetric data matrix $A$, where for distinct indices $i,j$, $A_{ij} \sim P$ if $i, j$ are both in the community and $A_{ij} \sim Q$ otherwise, for two known probability distributions $P$ and $Q$. We identify a sufficient condition and a necessary condition for the success of SDP for the general model. For both the Bernoulli case ($P={{\rm Bern}}(p)$ and $Q={{\rm Bern}}(q)$ with $p>q$) and the Gaussian case ($P=\mathcal{N}(\mu,1)$ and $Q=\mathcal{N}(0,1)$ with $\mu>0$), which correspond to the problem of planted dense subgraph recovery and submatrix localization respectively, the general results lead to the following findings: (1) If $K=\omega( n /\log n)$, SDP attains the information-theoretic recovery limits with sharp constants; (2) If $K=\Theta(n/\log n)$, SDP is order-wise optimal, but strictly suboptimal by a constant factor; (3) If $K=o(n/\log n)$ and $K \to \infty$, SDP is order-wise suboptimal. The same critical scaling for $K$ is found to hold, up to constant factors, for the performance of SDP on the stochastic block model of $n$ vertices partitioned into multiple communities of equal size $K$. A key ingredient in the proof of the necessary condition is a construction of a primal feasible solution based on random perturbation of the true cluster matrix.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge