Graph Alignment via Birkhoff Relaxation

We consider the graph alignment problem, wherein the objective is to find a vertex correspondence between two graphs that maximizes the edge overlap. The graph alignment problem is an instance of the quadratic assignment problem (QAP), known to be NP-hard in the worst case even to approximately solve. In this paper, we analyze Birkhoff relaxation, a tight convex relaxation of QAP, and present theoretical guarantees on its performance when the inputs follow the Gaussian Wigner Model. More specifically, the weighted adjacency matrices are correlated Gaussian Orthogonal Ensemble with correlation $1/\sqrt{1+\sigma^2}$. Denote the optimal solutions of the QAP and Birkhoff relaxation by $\Pi^\star$ and $X^\star$ respectively. We show that $\|X^\star-\Pi^\star\|_F^2 = o(n)$ when $\sigma = o(n^{-1.25})$ and $\|X^\star-\Pi^\star\|_F^2 = \Omega(n)$ when $\sigma = \Omega(n^{-0.5})$. Thus, the optimal solution $X^\star$ transitions from a small perturbation of $\Pi^\star$ for small $\sigma$ to being well separated from $\Pi^\star$ as $\sigma$ becomes larger than $n^{-0.5}$. This result allows us to guarantee that simple rounding procedures on $X^\star$ align $1-o(1)$ fraction of vertices correctly whenever $\sigma = o(n^{-1.25})$. This condition on $\sigma$ to ensure the success of the Birkhoff relaxation is state-of-the-art.

The feasibility of multi-graph alignment: a Bayesian approach

We establish thresholds for the feasibility of random multi-graph alignment in two models. In the Gaussian model, we demonstrate an "all-or-nothing" phenomenon: above a critical threshold, exact alignment is achievable with high probability, while below it, even partial alignment is statistically impossible. In the sparse Erd\H{o}s-R\'enyi model, we rigorously identify a threshold below which no meaningful partial alignment is possible and conjecture that above this threshold, partial alignment can be achieved. To prove these results, we develop a general Bayesian estimation framework over metric spaces, which provides insight into a broader class of high-dimensional statistical problems.

Meta-learning of shared linear representations beyond well-specified linear regression

Motivated by multi-task and meta-learning approaches, we consider the problem of learning structure shared by tasks or users, such as shared low-rank representations or clustered structures. While all previous works focus on well-specified linear regression, we consider more general convex objectives, where the structural low-rank and cluster assumptions are expressed on the optima of each function. We show that under mild assumptions such as \textit{Hessian concentration} and \textit{noise concentration at the optimum}, rank and clustered regularized estimators recover such structure, provided the number of samples per task and the number of tasks are large enough. We then study the problem of recovering the subspace in which all the solutions lie, in the setting where there is only a single sample per task: we show that in that case, the rank-constrained estimator can recover the subspace, but that the number of tasks needs to scale exponentially large with the dimension of the subspace. Finally, we provide a polynomial-time algorithm via nuclear norm constraints for learning a shared linear representation in the context of convex learning objectives.

In-depth Analysis of Low-rank Matrix Factorisation in a Federated Setting

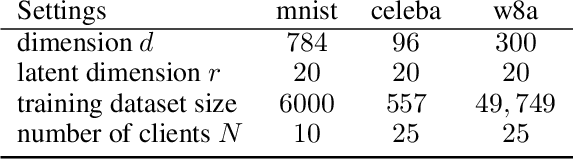
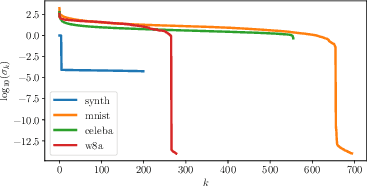
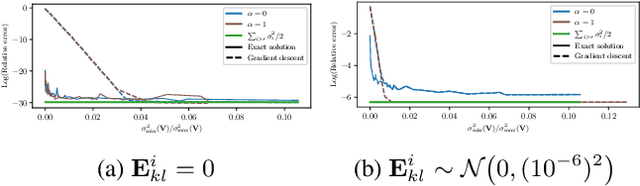
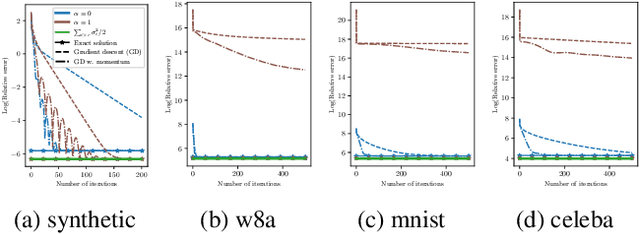
We analyze a distributed algorithm to compute a low-rank matrix factorization on $N$ clients, each holding a local dataset $\mathbf{S}^i \in \mathbb{R}^{n_i \times d}$, mathematically, we seek to solve $min_{\mathbf{U}^i \in \mathbb{R}^{n_i\times r}, \mathbf{V}\in \mathbb{R}^{d \times r} } \frac{1}{2} \sum_{i=1}^N \|\mathbf{S}^i - \mathbf{U}^i \mathbf{V}^\top\|^2_{\text{F}}$. Considering a power initialization of $\mathbf{V}$, we rewrite the previous smooth non-convex problem into a smooth strongly-convex problem that we solve using a parallel Nesterov gradient descent potentially requiring a single step of communication at the initialization step. For any client $i$ in $\{1, \dots, N\}$, we obtain a global $\mathbf{V}$ in $\mathbb{R}^{d \times r}$ common to all clients and a local variable $\mathbf{U}^i$ in $\mathbb{R}^{n_i \times r}$. We provide a linear rate of convergence of the excess loss which depends on $\sigma_{\max} / \sigma_{r}$, where $\sigma_{r}$ is the $r^{\mathrm{th}}$ singular value of the concatenation $\mathbf{S}$ of the matrices $(\mathbf{S}^i)_{i=1}^N$. This result improves the rates of convergence given in the literature, which depend on $\sigma_{\max}^2 / \sigma_{\min}^2$. We provide an upper bound on the Frobenius-norm error of reconstruction under the power initialization strategy. We complete our analysis with experiments on both synthetic and real data.

Aligning Embeddings and Geometric Random Graphs: Informational Results and Computational Approaches for the Procrustes-Wasserstein Problem

The Procrustes-Wasserstein problem consists in matching two high-dimensional point clouds in an unsupervised setting, and has many applications in natural language processing and computer vision. We consider a planted model with two datasets $X,Y$ that consist of $n$ datapoints in $\mathbb{R}^d$, where $Y$ is a noisy version of $X$, up to an orthogonal transformation and a relabeling of the data points. This setting is related to the graph alignment problem in geometric models. In this work, we focus on the euclidean transport cost between the point clouds as a measure of performance for the alignment. We first establish information-theoretic results, in the high ($d \gg \log n$) and low ($d \ll \log n$) dimensional regimes. We then study computational aspects and propose the Ping-Pong algorithm, alternatively estimating the orthogonal transformation and the relabeling, initialized via a Franke-Wolfe convex relaxation. We give sufficient conditions for the method to retrieve the planted signal after one single step. We provide experimental results to compare the proposed approach with the state-of-the-art method of Grave et al. (2019).

Asynchronous SGD on Graphs: a Unified Framework for Asynchronous Decentralized and Federated Optimization

Decentralized and asynchronous communications are two popular techniques to speedup communication complexity of distributed machine learning, by respectively removing the dependency over a central orchestrator and the need for synchronization. Yet, combining these two techniques together still remains a challenge. In this paper, we take a step in this direction and introduce Asynchronous SGD on Graphs (AGRAF SGD) -- a general algorithmic framework that covers asynchronous versions of many popular algorithms including SGD, Decentralized SGD, Local SGD, FedBuff, thanks to its relaxed communication and computation assumptions. We provide rates of convergence under much milder assumptions than previous decentralized asynchronous works, while still recovering or even improving over the best know results for all the algorithms covered.

Generalization Error of First-Order Methods for Statistical Learning with Generic Oracles

In this paper, we provide a novel framework for the analysis of generalization error of first-order optimization algorithms for statistical learning when the gradient can only be accessed through partial observations given by an oracle. Our analysis relies on the regularity of the gradient w.r.t. the data samples, and allows to derive near matching upper and lower bounds for the generalization error of multiple learning problems, including supervised learning, transfer learning, robust learning, distributed learning and communication efficient learning using gradient quantization. These results hold for smooth and strongly-convex optimization problems, as well as smooth non-convex optimization problems verifying a Polyak-Lojasiewicz assumption. In particular, our upper and lower bounds depend on a novel quantity that extends the notion of conditional standard deviation, and is a measure of the extent to which the gradient can be approximated by having access to the oracle. As a consequence, our analysis provides a precise meaning to the intuition that optimization of the statistical learning objective is as hard as the estimation of its gradient. Finally, we show that, in the case of standard supervised learning, mini-batch gradient descent with increasing batch sizes and a warm start can reach a generalization error that is optimal up to a multiplicative factor, thus motivating the use of this optimization scheme in practical applications.

Statistical limits of correlation detection in trees

In this paper we address the problem of testing whether two observed trees $(t,t')$ are sampled either independently or from a joint distribution under which they are correlated. This problem, which we refer to as correlation detection in trees, plays a key role in the study of graph alignment for two correlated random graphs. Motivated by graph alignment, we investigate the conditions of existence of one-sided tests, i.e. tests which have vanishing type I error and non-vanishing power in the limit of large tree depth. For the correlated Galton-Watson model with Poisson offspring of mean $\lambda>0$ and correlation parameter $s \in (0,1)$, we identify a phase transition in the limit of large degrees at $s = \sqrt{\alpha}$, where $\alpha \sim 0.3383$ is Otter's constant. Namely, we prove that no such test exists for $s \leq \sqrt{\alpha}$, and that such a test exists whenever $s > \sqrt{\alpha}$, for $\lambda$ large enough. This result sheds new light on the graph alignment problem in the sparse regime (with $O(1)$ average node degrees) and on the performance of the MPAlign method studied in Ganassali et al. (2021), Piccioli et al. (2021), proving in particular the conjecture of Piccioli et al. (2021) that MPAlign succeeds in the partial recovery task for correlation parameter $s>\sqrt{\alpha}$ provided the average node degree $\lambda$ is large enough.

Muffliato: Peer-to-Peer Privacy Amplification for Decentralized Optimization and Averaging

Decentralized optimization is increasingly popular in machine learning for its scalability and efficiency. Intuitively, it should also provide better privacy guarantees, as nodes only observe the messages sent by their neighbors in the network graph. But formalizing and quantifying this gain is challenging: existing results are typically limited to Local Differential Privacy (LDP) guarantees that overlook the advantages of decentralization. In this work, we introduce pairwise network differential privacy, a relaxation of LDP that captures the fact that the privacy leakage from a node $u$ to a node $v$ may depend on their relative position in the graph. We then analyze the combination of local noise injection with (simple or randomized) gossip averaging protocols on fixed and random communication graphs. We also derive a differentially private decentralized optimization algorithm that alternates between local gradient descent steps and gossip averaging. Our results show that our algorithms amplify privacy guarantees as a function of the distance between nodes in the graph, matching the privacy-utility trade-off of the trusted curator, up to factors that explicitly depend on the graph topology. Finally, we illustrate our privacy gains with experiments on synthetic and real-world datasets.

Correlation detection in trees for partial graph alignment

We consider alignment of sparse graphs, which consists in finding a mapping between the nodes of two graphs which preserves most of the edges. Our approach is to compare local structures in the two graphs, matching two nodes if their neighborhoods are 'close enough': for correlated Erd\H{o}s-R\'enyi random graphs, this problem can be locally rephrased in terms of testing whether a pair of branching trees is drawn from either a product distribution, or a correlated distribution. We design an optimal test for this problem which gives rise to a message-passing algorithm for graph alignment, which provably returns in polynomial time a positive fraction of correctly matched vertices, and a vanishing fraction of mismatches. With an average degree $\lambda = O(1)$ in the graphs, and a correlation parameter $s \in [0,1]$, this result holds with $\lambda s$ large enough, and $1-s$ small enough, completing the recent state-of-the-art diagram. Tighter conditions for determining whether partial graph alignment (or correlation detection in trees) is feasible in polynomial time are given in terms of Kullback-Leibler divergences.