Differentiable short-time Fourier transform with respect to the hop length

In this paper, we propose a differentiable version of the short-time Fourier transform (STFT) that allows for gradient-based optimization of the hop length or the frame temporal position by making these parameters continuous. Our approach provides improved control over the temporal positioning of frames, as the continuous nature of the hop length allows for a more finely-tuned optimization. Furthermore, our contribution enables the use of optimization methods such as gradient descent, which are more computationally efficient than conventional discrete optimization methods. Our differentiable STFT can also be easily integrated into existing algorithms and neural networks. We present a simulated illustration to demonstrate the efficacy of our approach and to garner interest from the research community.

Differentiable adaptive short-time Fourier transform with respect to the window length

This paper presents a gradient-based method for on-the-fly optimization for both per-frame and per-frequency window length of the short-time Fourier transform (STFT), related to previous work in which we developed a differentiable version of STFT by making the window length a continuous parameter. The resulting differentiable adaptive STFT possesses commendable properties, such as the ability to adapt in the same time-frequency representation to both transient and stationary components, while being easily optimized by gradient descent. We validate the performance of our method in vibration analysis.

A differentiable short-time Fourier transform with respect to the window length

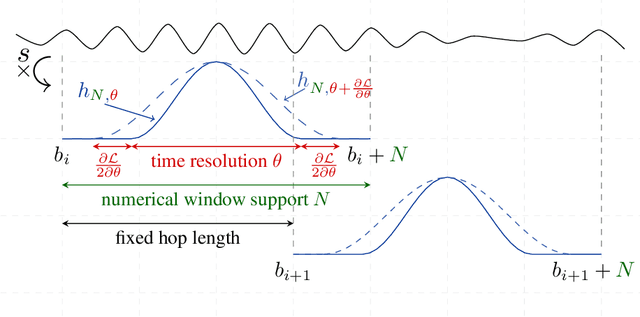
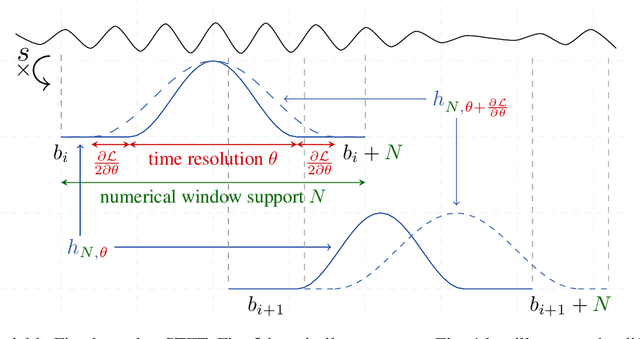
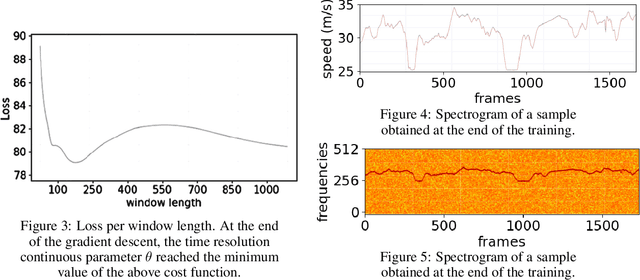
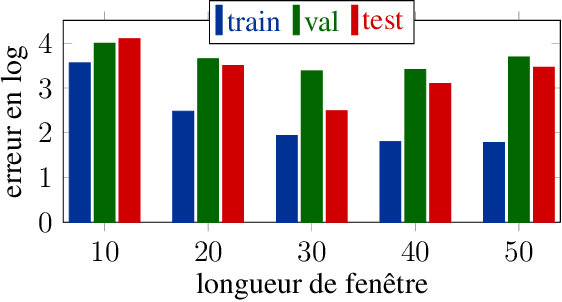
In this paper, we revisit the use of spectrograms in neural networks, by making the window length a continuous parameter optimizable by gradient descent instead of an empirically tuned integer-valued hyperparameter. The contribution is mostly theoretical at this point, but plugging the modified STFT into any existing neural network is straightforward. We first define a differentiable version of the STFT in the case where local bins centers are fixed and independent of the window length parameter. We then discuss the more difficult case where the window length affects the position and number of bins. We illustrate the benefits of this new tool on an estimation and a classification problems, showing it can be of interest not only to neural networks but to any STFT-based signal processing algorithm.

A Variational Bayesian Approach for Image Restoration. Application to Image Deblurring with Poisson-Gaussian Noise

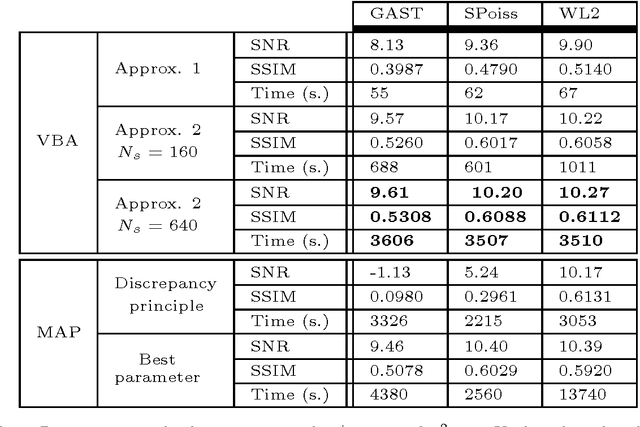
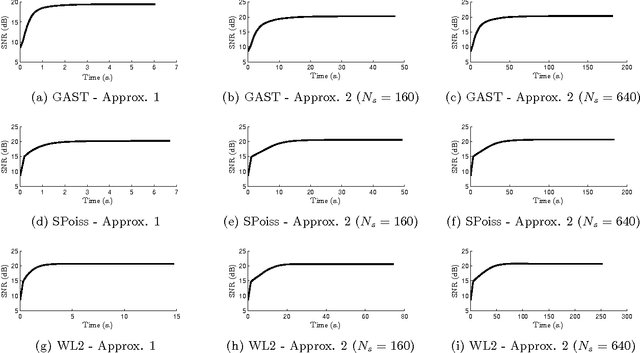
In this paper, a methodology is investigated for signal recovery in the presence of non-Gaussian noise. In contrast with regularized minimization approaches often adopted in the literature, in our algorithm the regularization parameter is reliably estimated from the observations. As the posterior density of the unknown parameters is analytically intractable, the estimation problem is derived in a variational Bayesian framework where the goal is to provide a good approximation to the posterior distribution in order to compute posterior mean estimates. Moreover, a majorization technique is employed to circumvent the difficulties raised by the intricate forms of the non-Gaussian likelihood and of the prior density. We demonstrate the potential of the proposed approach through comparisons with state-of-the-art techniques that are specifically tailored to signal recovery in the presence of mixed Poisson-Gaussian noise. Results show that the proposed approach is efficient and achieves performance comparable with other methods where the regularization parameter is manually tuned from the ground truth.