Yuling Zheng
A Variational Bayesian Approach for Image Restoration. Application to Image Deblurring with Poisson-Gaussian Noise
Jan 20, 2017

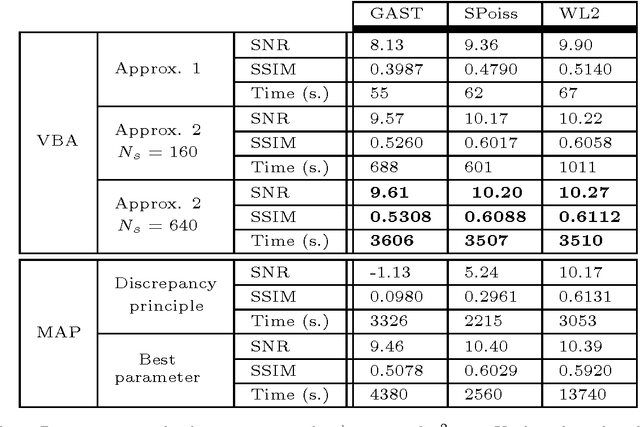
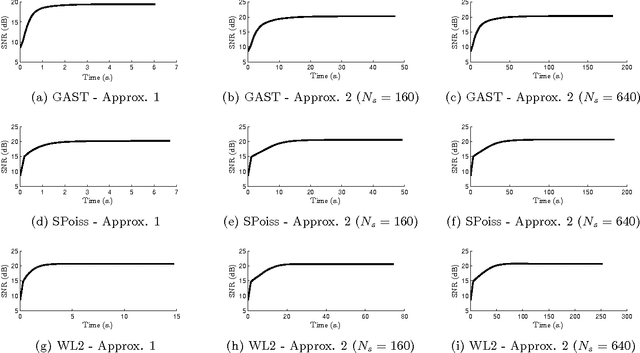
Abstract:In this paper, a methodology is investigated for signal recovery in the presence of non-Gaussian noise. In contrast with regularized minimization approaches often adopted in the literature, in our algorithm the regularization parameter is reliably estimated from the observations. As the posterior density of the unknown parameters is analytically intractable, the estimation problem is derived in a variational Bayesian framework where the goal is to provide a good approximation to the posterior distribution in order to compute posterior mean estimates. Moreover, a majorization technique is employed to circumvent the difficulties raised by the intricate forms of the non-Gaussian likelihood and of the prior density. We demonstrate the potential of the proposed approach through comparisons with state-of-the-art techniques that are specifically tailored to signal recovery in the presence of mixed Poisson-Gaussian noise. Results show that the proposed approach is efficient and achieves performance comparable with other methods where the regularization parameter is manually tuned from the ground truth.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge