In-depth Analysis of Low-rank Matrix Factorisation in a Federated Setting

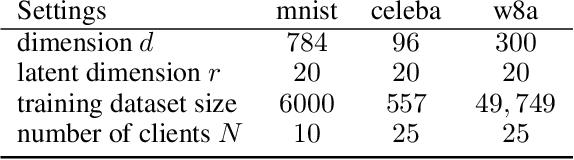
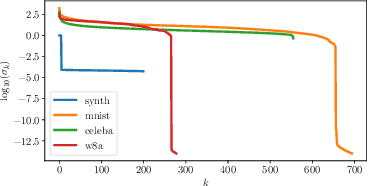
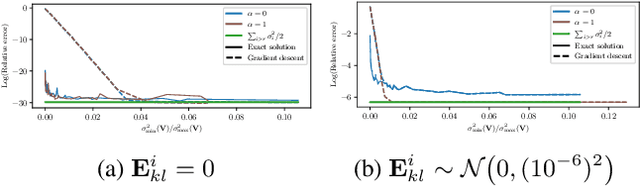
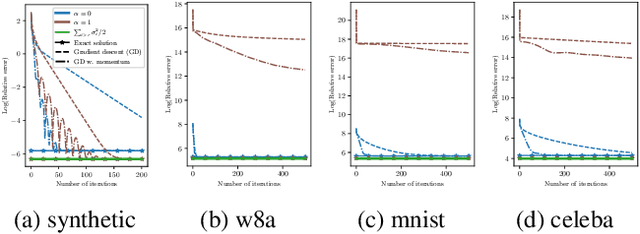
We analyze a distributed algorithm to compute a low-rank matrix factorization on $N$ clients, each holding a local dataset $\mathbf{S}^i \in \mathbb{R}^{n_i \times d}$, mathematically, we seek to solve $min_{\mathbf{U}^i \in \mathbb{R}^{n_i\times r}, \mathbf{V}\in \mathbb{R}^{d \times r} } \frac{1}{2} \sum_{i=1}^N \|\mathbf{S}^i - \mathbf{U}^i \mathbf{V}^\top\|^2_{\text{F}}$. Considering a power initialization of $\mathbf{V}$, we rewrite the previous smooth non-convex problem into a smooth strongly-convex problem that we solve using a parallel Nesterov gradient descent potentially requiring a single step of communication at the initialization step. For any client $i$ in $\{1, \dots, N\}$, we obtain a global $\mathbf{V}$ in $\mathbb{R}^{d \times r}$ common to all clients and a local variable $\mathbf{U}^i$ in $\mathbb{R}^{n_i \times r}$. We provide a linear rate of convergence of the excess loss which depends on $\sigma_{\max} / \sigma_{r}$, where $\sigma_{r}$ is the $r^{\mathrm{th}}$ singular value of the concatenation $\mathbf{S}$ of the matrices $(\mathbf{S}^i)_{i=1}^N$. This result improves the rates of convergence given in the literature, which depend on $\sigma_{\max}^2 / \sigma_{\min}^2$. We provide an upper bound on the Frobenius-norm error of reconstruction under the power initialization strategy. We complete our analysis with experiments on both synthetic and real data.

Compressed and distributed least-squares regression: convergence rates with applications to Federated Learning

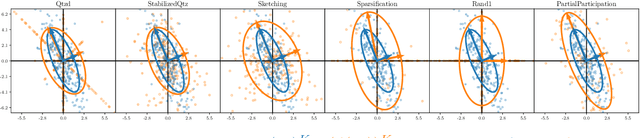
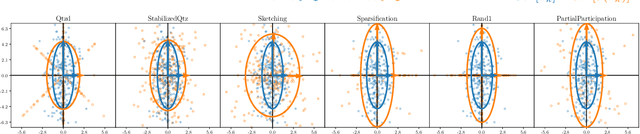
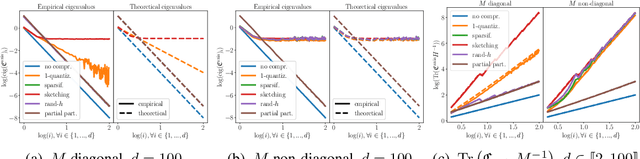
In this paper, we investigate the impact of compression on stochastic gradient algorithms for machine learning, a technique widely used in distributed and federated learning. We underline differences in terms of convergence rates between several unbiased compression operators, that all satisfy the same condition on their variance, thus going beyond the classical worst-case analysis. To do so, we focus on the case of least-squares regression (LSR) and analyze a general stochastic approximation algorithm for minimizing quadratic functions relying on a random field. We consider weak assumptions on the random field, tailored to the analysis (specifically, expected H\"older regularity), and on the noise covariance, enabling the analysis of various randomizing mechanisms, including compression. We then extend our results to the case of federated learning. More formally, we highlight the impact on the convergence of the covariance $\mathfrak{C}_{\mathrm{ania}}$ of the additive noise induced by the algorithm. We demonstrate despite the non-regularity of the stochastic field, that the limit variance term scales with $\mathrm{Tr}(\mathfrak{C}_{\mathrm{ania}} H^{-1})/K$ (where $H$ is the Hessian of the optimization problem and $K$ the number of iterations) generalizing the rate for the vanilla LSR case where it is $\sigma^2 \mathrm{Tr}(H H^{-1}) / K = \sigma^2 d / K$ (Bach and Moulines, 2013). Then, we analyze the dependency of $\mathfrak{C}_{\mathrm{ania}}$ on the compression strategy and ultimately its impact on convergence, first in the centralized case, then in two heterogeneous FL frameworks.

FLamby: Datasets and Benchmarks for Cross-Silo Federated Learning in Realistic Healthcare Settings

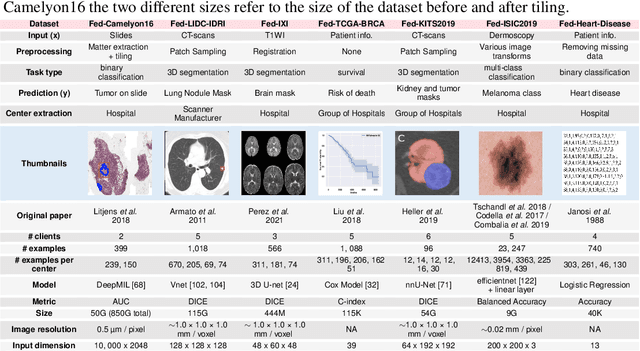
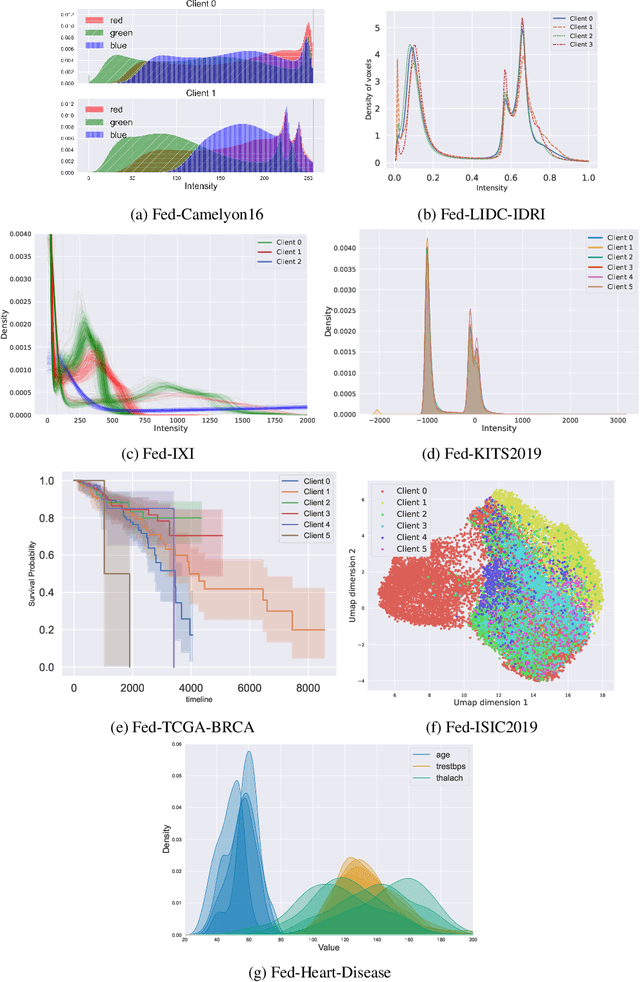
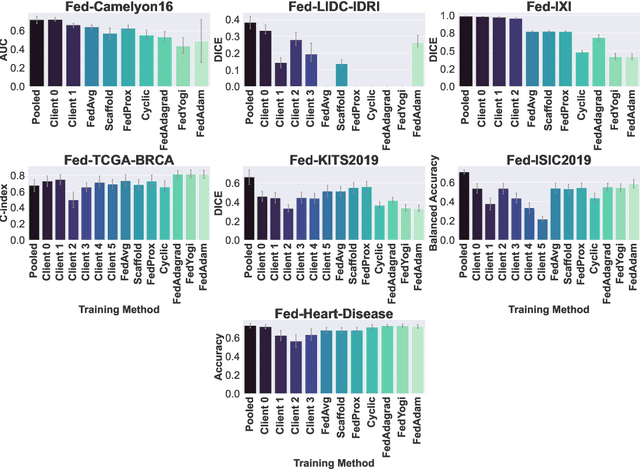
Federated Learning (FL) is a novel approach enabling several clients holding sensitive data to collaboratively train machine learning models, without centralizing data. The cross-silo FL setting corresponds to the case of few ($2$--$50$) reliable clients, each holding medium to large datasets, and is typically found in applications such as healthcare, finance, or industry. While previous works have proposed representative datasets for cross-device FL, few realistic healthcare cross-silo FL datasets exist, thereby slowing algorithmic research in this critical application. In this work, we propose a novel cross-silo dataset suite focused on healthcare, FLamby (Federated Learning AMple Benchmark of Your cross-silo strategies), to bridge the gap between theory and practice of cross-silo FL. FLamby encompasses 7 healthcare datasets with natural splits, covering multiple tasks, modalities, and data volumes, each accompanied with baseline training code. As an illustration, we additionally benchmark standard FL algorithms on all datasets. Our flexible and modular suite allows researchers to easily download datasets, reproduce results and re-use the different components for their research. FLamby is available at~\url{www.github.com/owkin/flamby}.

Preserved central model for faster bidirectional compression in distributed settings

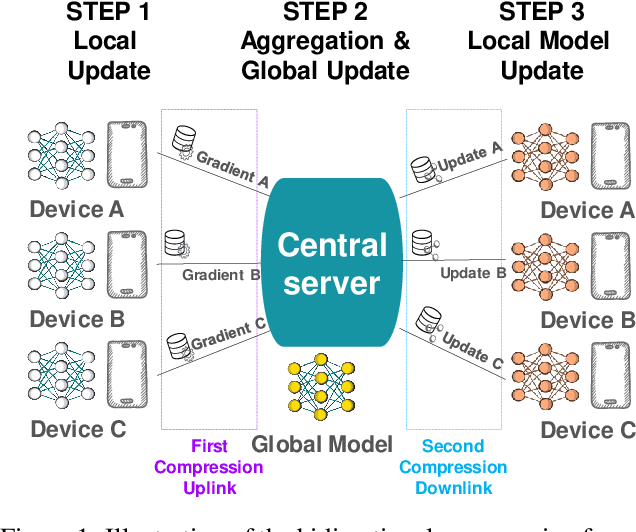
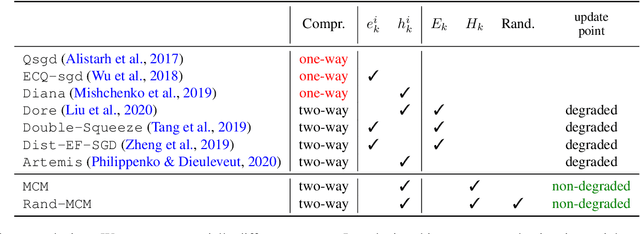
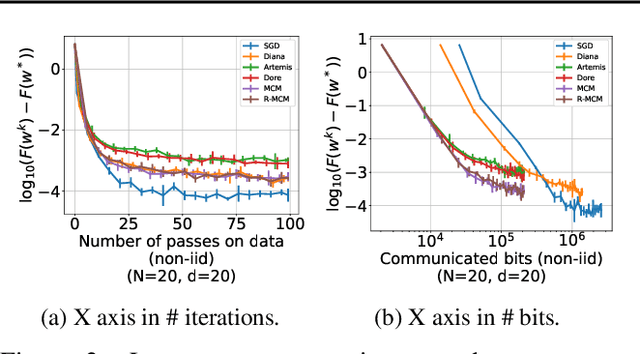
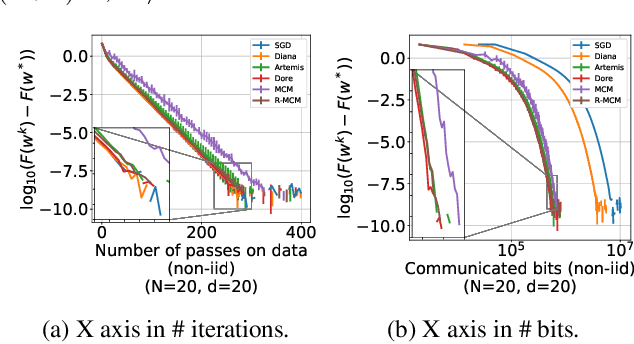
We develop a new approach to tackle communication constraints in a distributed learning problem with a central server. We propose and analyze a new algorithm that performs bidirectional compression and achieves the same convergence rate as algorithms using only uplink (from the local workers to the central server) compression. To obtain this improvement, we design MCM, an algorithm such that the downlink compression only impacts local models, while the global model is preserved. As a result, and contrary to previous works, the gradients on local servers are computed on perturbed models. Consequently, convergence proofs are more challenging and require a precise control of this perturbation. To ensure it, MCM additionally combines model compression with a memory mechanism. This analysis opens new doors, e.g. incorporating worker dependent randomized-models and partial participation.

Artemis: tight convergence guarantees for bidirectional compression in Federated Learning

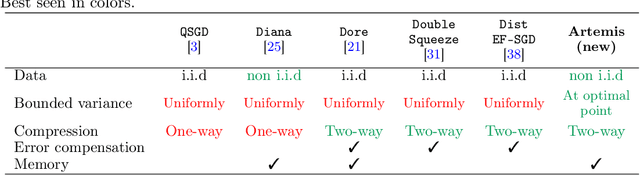
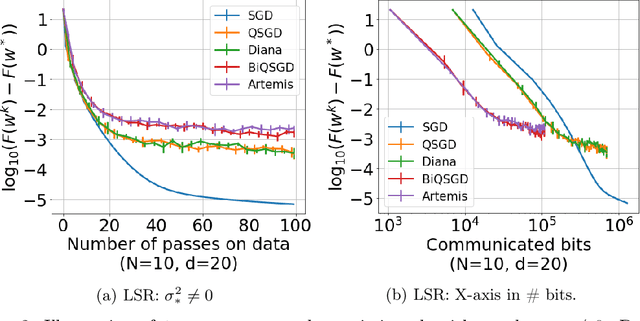
We introduce a new algorithm - Artemis - tackling the problem of learning in a distributed framework with communication constraints. Several workers perform the optimization process using a central server to aggregate their computation. To alleviate the communication cost, Artemis compresses the information sent in both directions (from the workers to the server and conversely) combined with a memory mechanism. It improves on existing quantized federated learning algorithms that only consider unidirectional compression (to the server), or use very strong assumptions on the compression operator. We provide fast rates of convergence (linear up to a threshold) under weak assumptions on the stochastic gradients (noise's variance bounded only at optimal point) in non-i.i.d. setting, highlight the impact of memory for unidirectional and bidirectional compression, analyze Polyak-Ruppert averaging, use convergence in distribution to obtain a lower bound of the asymptotic variance that highlights practical limits of compression, and provide experimental results to demonstrate the validity of our analysis.