Preserved central model for faster bidirectional compression in distributed settings
Paper and Code
Feb 24, 2021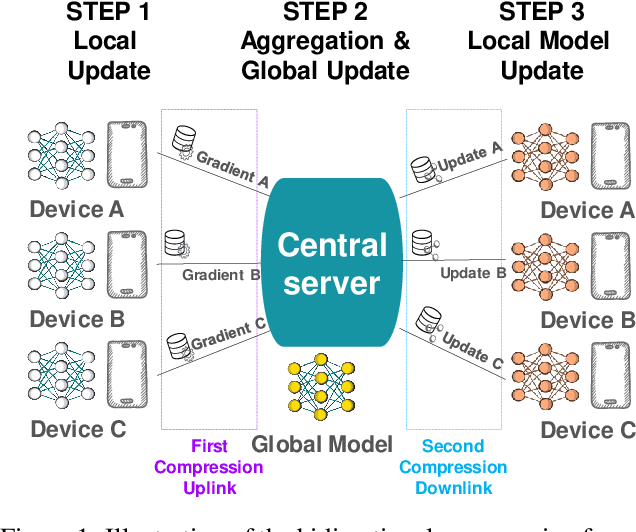
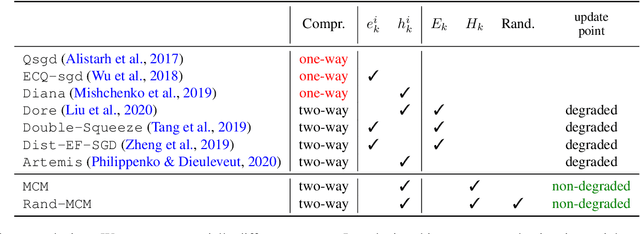
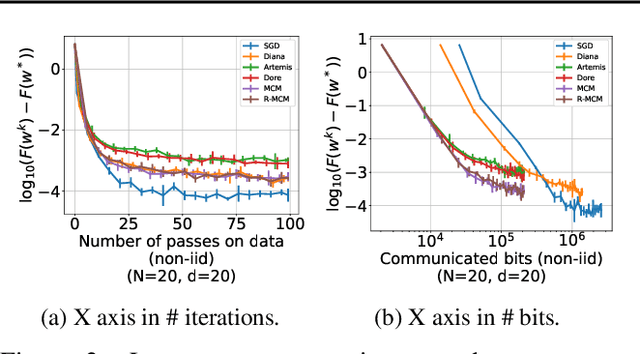
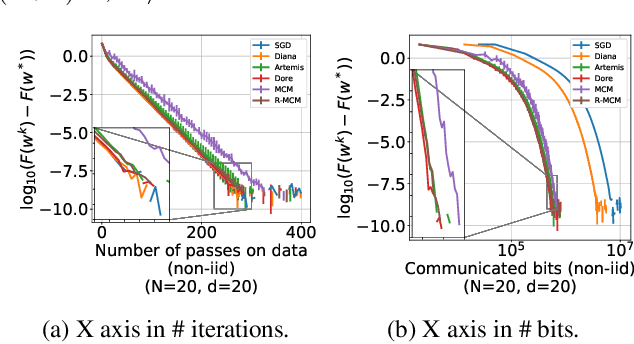
We develop a new approach to tackle communication constraints in a distributed learning problem with a central server. We propose and analyze a new algorithm that performs bidirectional compression and achieves the same convergence rate as algorithms using only uplink (from the local workers to the central server) compression. To obtain this improvement, we design MCM, an algorithm such that the downlink compression only impacts local models, while the global model is preserved. As a result, and contrary to previous works, the gradients on local servers are computed on perturbed models. Consequently, convergence proofs are more challenging and require a precise control of this perturbation. To ensure it, MCM additionally combines model compression with a memory mechanism. This analysis opens new doors, e.g. incorporating worker dependent randomized-models and partial participation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge