Artemis: tight convergence guarantees for bidirectional compression in Federated Learning

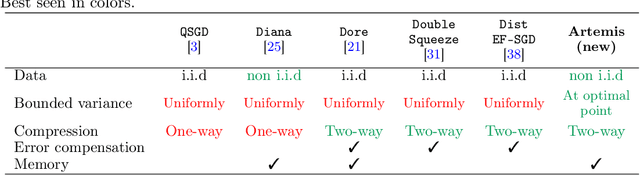
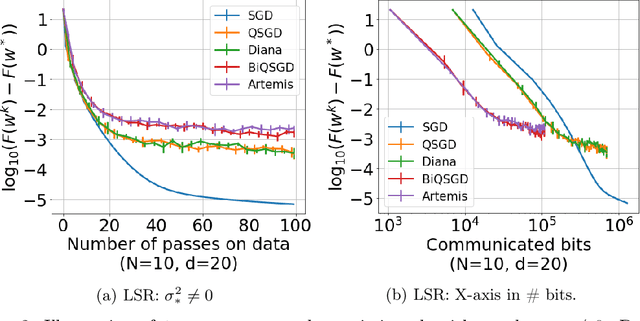
We introduce a new algorithm - Artemis - tackling the problem of learning in a distributed framework with communication constraints. Several workers perform the optimization process using a central server to aggregate their computation. To alleviate the communication cost, Artemis compresses the information sent in both directions (from the workers to the server and conversely) combined with a memory mechanism. It improves on existing quantized federated learning algorithms that only consider unidirectional compression (to the server), or use very strong assumptions on the compression operator. We provide fast rates of convergence (linear up to a threshold) under weak assumptions on the stochastic gradients (noise's variance bounded only at optimal point) in non-i.i.d. setting, highlight the impact of memory for unidirectional and bidirectional compression, analyze Polyak-Ruppert averaging, use convergence in distribution to obtain a lower bound of the asymptotic variance that highlights practical limits of compression, and provide experimental results to demonstrate the validity of our analysis.