Metric space valued Fréchet regression

We consider the problem of estimating the Fréchet and conditional Fréchet mean from data taking values in separable metric spaces. Unlike Euclidean spaces, where well-established methods are available, there is no practical estimator that works universally for all metric spaces. Therefore, we introduce a computable estimator for the Fréchet mean based on random quantization techniques and establish its universal consistency across any separable metric spaces. Additionally, we propose another estimator for the conditional Fréchet mean, leveraging data-driven partitioning and quantization, and demonstrate its universal consistency when the output space is any Banach space.

Adaptive collaboration for online personalized distributed learning with heterogeneous clients

We study the problem of online personalized decentralized learning with $N$ statistically heterogeneous clients collaborating to accelerate local training. An important challenge in this setting is to select relevant collaborators to reduce gradient variance while mitigating the introduced bias. To tackle this, we introduce a gradient-based collaboration criterion, allowing each client to dynamically select peers with similar gradients during the optimization process. Our criterion is motivated by a refined and more general theoretical analysis of the All-for-one algorithm, proved to be optimal in Even et al. (2022) for an oracle collaboration scheme. We derive excess loss upper-bounds for smooth objective functions, being either strongly convex, non-convex, or satisfying the Polyak-Lojasiewicz condition; our analysis reveals that the algorithm acts as a variance reduction method where the speed-up depends on a sufficient variance. We put forward two collaboration methods instantiating the proposed general schema; and we show that one variant preserves the optimality of All-for-one. We validate our results with experiments on synthetic and real datasets.

TAMIS: Tailored Membership Inference Attacks on Synthetic Data

Membership Inference Attacks (MIA) enable to empirically assess the privacy of a machine learning algorithm. In this paper, we propose TAMIS, a novel MIA against differentially-private synthetic data generation methods that rely on graphical models. This attack builds upon MAMA-MIA, a recently-published state-of-the-art method. It lowers its computational cost and requires less attacker knowledge. Our attack is the product of a two-fold improvement. First, we recover the graphical model having generated a synthetic dataset by using solely that dataset, rather than shadow-modeling over an auxiliary one. This proves less costly and more performant. Second, we introduce a more mathematically-grounded attack score, that provides a natural threshold for binary predictions. In our experiments, TAMIS achieves better or similar performance as MAMA-MIA on replicas of the SNAKE challenge.

Marginal and training-conditional guarantees in one-shot federated conformal prediction

We study conformal prediction in the one-shot federated learning setting. The main goal is to compute marginally and training-conditionally valid prediction sets, at the server-level, in only one round of communication between the agents and the server. Using the quantile-of-quantiles family of estimators and split conformal prediction, we introduce a collection of computationally-efficient and distribution-free algorithms that satisfy the aforementioned requirements. Our approaches come from theoretical results related to order statistics and the analysis of the Beta-Beta distribution. We also prove upper bounds on the coverage of all proposed algorithms when the nonconformity scores are almost surely distinct. For algorithms with training-conditional guarantees, these bounds are of the same order of magnitude as those of the centralized case. Remarkably, this implies that the one-shot federated learning setting entails no significant loss compared to the centralized case. Our experiments confirm that our algorithms return prediction sets with coverage and length similar to those obtained in a centralized setting.

Improved Stability and Generalization Analysis of the Decentralized SGD Algorithm

This paper presents a new generalization error analysis for the Decentralized Stochastic Gradient Descent (D-SGD) algorithm based on algorithmic stability. The obtained results largely improve upon state-of-the-art results, and even invalidate their claims that the communication graph has a detrimental effect on generalization. For instance, we show that in convex settings, D-SGD has the same generalization bounds as the classical SGD algorithm, no matter the choice of graph. We exhibit that this counter-intuitive result comes from considering the average of local parameters, which hides a final global averaging step incompatible with the decentralized scenario. In light of this observation, we advocate to analyze the supremum over local parameters and show that in this case, the graph does have an impact on the generalization. Unlike prior results, our analysis yields non-vacuous bounds even for non-connected graphs.

One-Shot Federated Conformal Prediction

In this paper, we introduce a conformal prediction method to construct prediction sets in a oneshot federated learning setting. More specifically, we define a quantile-of-quantiles estimator and prove that for any distribution, it is possible to output prediction sets with desired coverage in only one round of communication. To mitigate privacy issues, we also describe a locally differentially private version of our estimator. Finally, over a wide range of experiments, we show that our method returns prediction sets with coverage and length very similar to those obtained in a centralized setting. Overall, these results demonstrate that our method is particularly well-suited to perform conformal predictions in a one-shot federated learning setting.

Robust Kernel Density Estimation with Median-of-Means principle

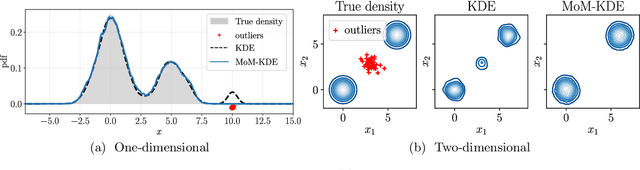
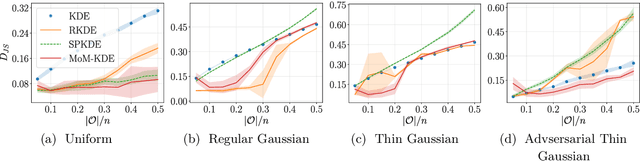
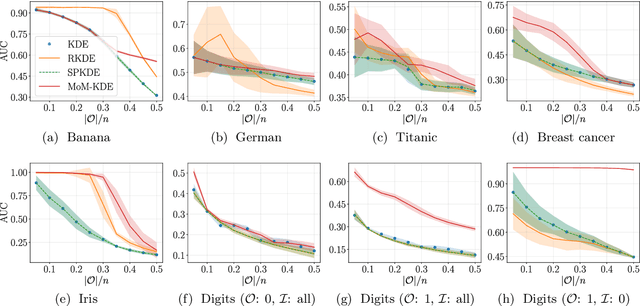
In this paper, we introduce a robust nonparametric density estimator combining the popular Kernel Density Estimation method and the Median-of-Means principle (MoM-KDE). This estimator is shown to achieve robustness to any kind of anomalous data, even in the case of adversarial contamination. In particular, while previous works only prove consistency results under known contamination model, this work provides finite-sample high-probability error-bounds without a priori knowledge on the outliers. Finally, when compared with other robust kernel estimators, we show that MoM-KDE achieves competitive results while having significant lower computational complexity.

Detecting multiple change-points in the time-varying Ising model

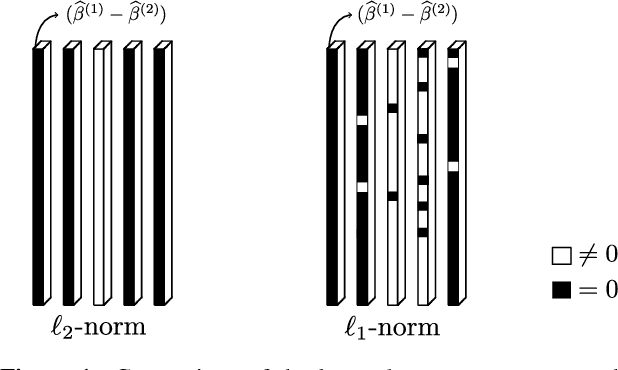
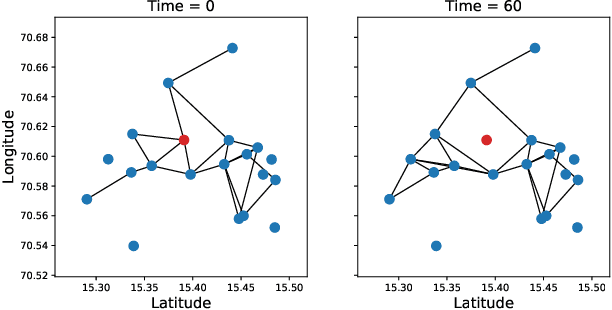
This work focuses on the estimation of change-points in a time-varying Ising graphical model (outputs $-1$ or $1$) evolving in a piecewise constant fashion. The occurring changes alter the graphical structure of the model, a structure which we also estimate in the present paper. For this purpose, we propose a new optimization program consisting in the minimization of a penalized negative conditional log-likelihood. The objective of the penalization is twofold: it imposes the learned graphs to be sparse and, thanks to a fused-type penalty, it enforces them to evolve piecewise constantly. Using few assumptions, we then give a change-point consistency theorem. Up to our knowledge, we are the first to present such theoretical result in the context of time-varying Ising model. Finally, experimental results on several synthetic examples and a real-world dataset demonstrate the empirical performance of our method.

A Probabilistic Framework to Node-level Anomaly Detection in Communication Networks

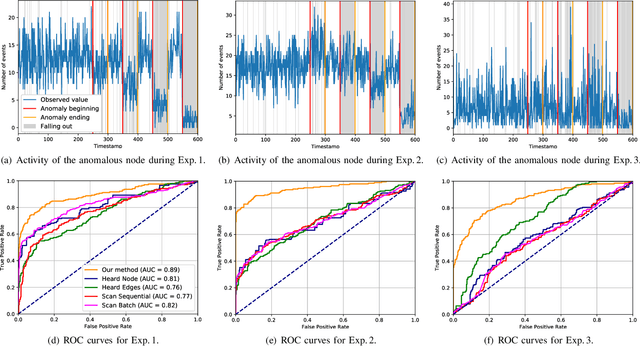
In this paper we consider the task of detecting abnormal communication volume occurring at node-level in communication networks. The signal of the communication activity is modeled by means of a clique stream: each occurring communication event is instantaneous and activates an undirected subgraph spanning over a set of equally participating nodes. We present a probabilistic framework to model and assess the communication volume observed at any single node. Specifically, we employ non-parametric regression to learn the probability that a node takes part in a certain event knowing the set of other nodes that are involved. On the top of that, we present a concentration inequality around the estimated volume of events in which a node could participate, which in turn allows us to build an efficient and interpretable anomaly scoring function. Finally, the superior performance of the proposed approach is empirically demonstrated in real-world sensor network data, as well as using synthetic communication activity that is in accordance with that latter setting.