Marginal and training-conditional guarantees in one-shot federated conformal prediction

We study conformal prediction in the one-shot federated learning setting. The main goal is to compute marginally and training-conditionally valid prediction sets, at the server-level, in only one round of communication between the agents and the server. Using the quantile-of-quantiles family of estimators and split conformal prediction, we introduce a collection of computationally-efficient and distribution-free algorithms that satisfy the aforementioned requirements. Our approaches come from theoretical results related to order statistics and the analysis of the Beta-Beta distribution. We also prove upper bounds on the coverage of all proposed algorithms when the nonconformity scores are almost surely distinct. For algorithms with training-conditional guarantees, these bounds are of the same order of magnitude as those of the centralized case. Remarkably, this implies that the one-shot federated learning setting entails no significant loss compared to the centralized case. Our experiments confirm that our algorithms return prediction sets with coverage and length similar to those obtained in a centralized setting.

One-Shot Federated Conformal Prediction

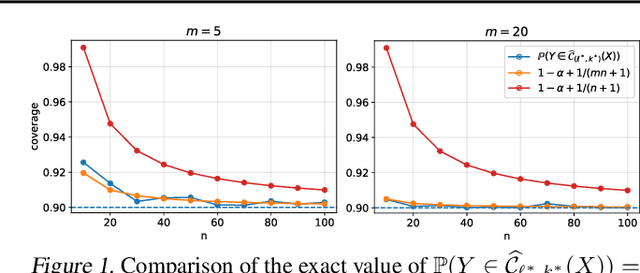
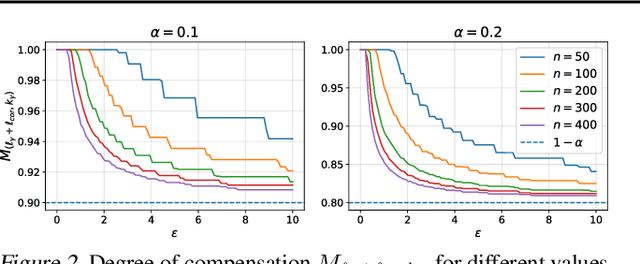
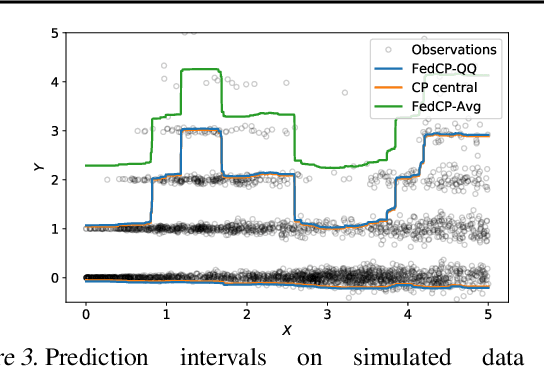
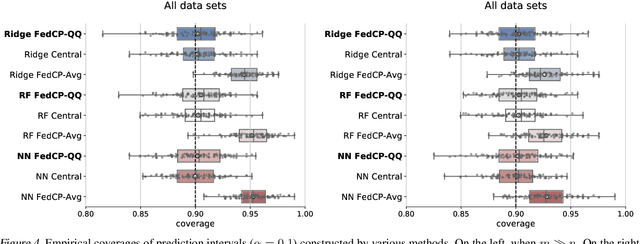
In this paper, we introduce a conformal prediction method to construct prediction sets in a oneshot federated learning setting. More specifically, we define a quantile-of-quantiles estimator and prove that for any distribution, it is possible to output prediction sets with desired coverage in only one round of communication. To mitigate privacy issues, we also describe a locally differentially private version of our estimator. Finally, over a wide range of experiments, we show that our method returns prediction sets with coverage and length very similar to those obtained in a centralized setting. Overall, these results demonstrate that our method is particularly well-suited to perform conformal predictions in a one-shot federated learning setting.

A Conditional Randomization Test for Sparse Logistic Regression in High-Dimension

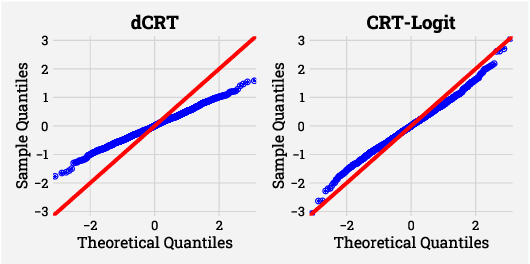
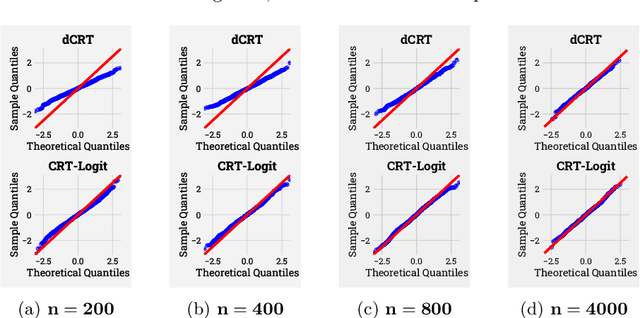
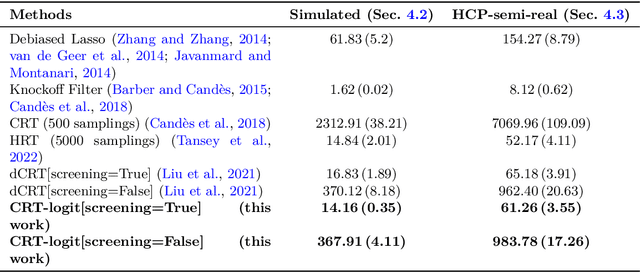
Identifying the relevant variables for a classification model with correct confidence levels is a central but difficult task in high-dimension. Despite the core role of sparse logistic regression in statistics and machine learning, it still lacks a good solution for accurate inference in the regime where the number of features $p$ is as large as or larger than the number of samples $n$. Here, we tackle this problem by improving the Conditional Randomization Test (CRT). The original CRT algorithm shows promise as a way to output p-values while making few assumptions on the distribution of the test statistics. As it comes with a prohibitive computational cost even in mildly high-dimensional problems, faster solutions based on distillation have been proposed. Yet, they rely on unrealistic hypotheses and result in low-power solutions. To improve this, we propose \emph{CRT-logit}, an algorithm that combines a variable-distillation step and a decorrelation step that takes into account the geometry of $\ell_1$-penalized logistic regression problem. We provide a theoretical analysis of this procedure, and demonstrate its effectiveness on simulations, along with experiments on large-scale brain-imaging and genomics datasets.

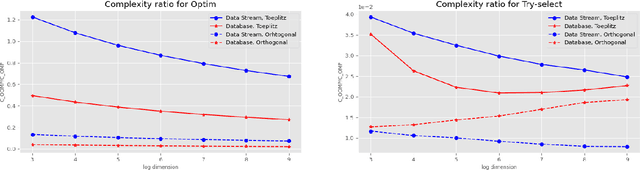
Online Orthogonal Matching Pursuit

Greedy algorithms for feature selection are widely used for recovering sparse high-dimensional vectors in linear models. In classical procedures, the main emphasis was put on the sample complexity, with little or no consideration of the computation resources required. We present a novel online algorithm: Online Orthogonal Matching Pursuit (OOMP) for online support recovery in the random design setting of sparse linear regression. Our procedure selects features sequentially, alternating between allocation of samples only as needed to candidate features, and optimization over the selected set of variables to estimate the regression coefficients. Theoretical guarantees about the output of this algorithm are proven and its computational complexity is analysed.

Aggregation of Multiple Knockoffs

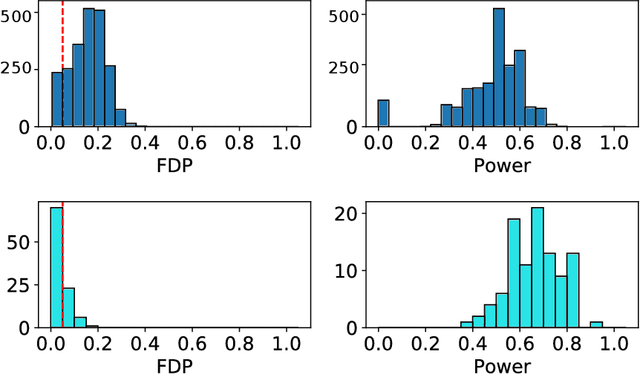
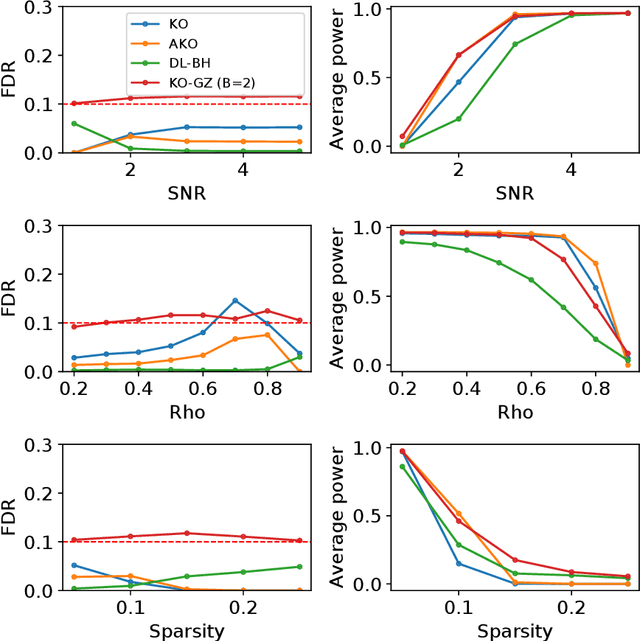
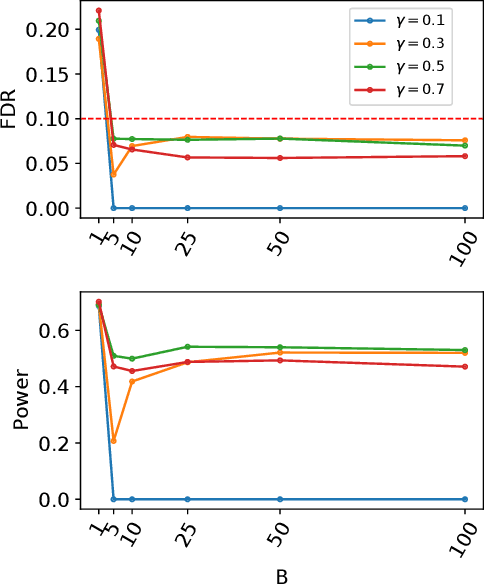
We develop an extension of the Knockoff Inference procedure, introduced by Barber and Candes (2015). This new method, called Aggregation of Multiple Knockoffs (AKO), addresses the instability inherent to the random nature of Knockoff-based inference. Specifically, AKO improves both the stability and power compared with the original Knockoff algorithm while still maintaining guarantees for False Discovery Rate control. We provide a new inference procedure, prove its core properties, and demonstrate its benefits in a set of experiments on synthetic and real datasets.

Rejoinder on: Minimal penalties and the slope heuristics: a survey

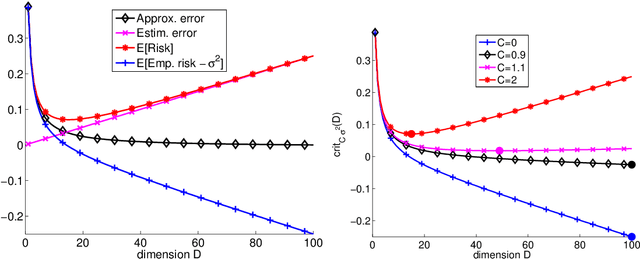
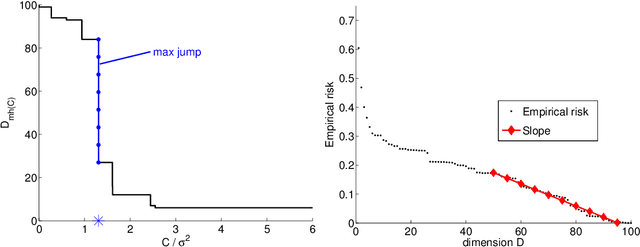
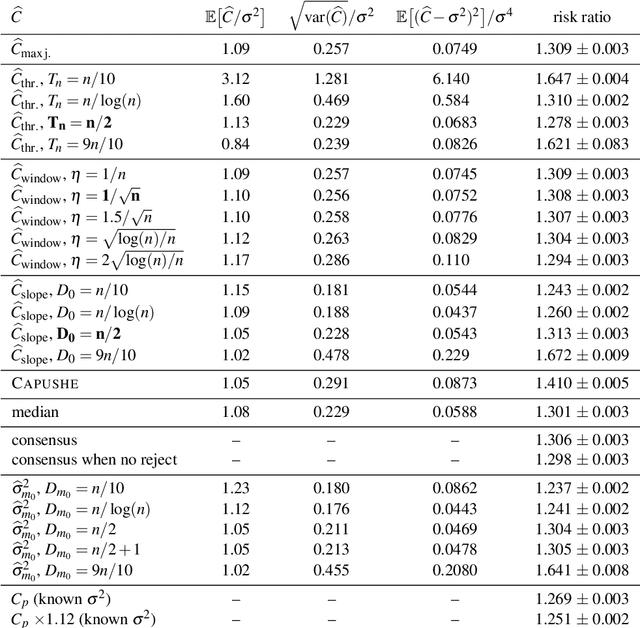
This text is the rejoinder following the discussion of a survey paper about minimal penalties and the slope heuristics (Arlot, 2019. Minimal penalties and the slope heuristics: a survey. Journal de la SFDS). While commenting on the remarks made by the discussants, it provides two new results about the slope heuristics for model selection among a collection of projection estimators in least-squares fixed-design regression. First, we prove that the slope heuristics works even when all models are significantly biased. Second, when the noise is Gaussian with a general dependence structure, we compute expectations of key quantities, showing that the slope heuristics certainly is valid in this setting also.

Minimal penalties and the slope heuristics: a survey

Birg{\'e} and Massart proposed in 2001 the slope heuristics as a way to choose optimally from data an unknown multiplicative constant in front of a penalty. It is built upon the notion of minimal penalty, and it has been generalized since to some 'minimal-penalty algorithms'. This paper reviews the theoretical results obtained for such algorithms, with a self-contained proof in the simplest framework, precise proof ideas for further generalizations, and a few new results. Explicit connections are made with residual-variance estimators-with an original contribution on this topic, showing that for this task the slope heuristics performs almost as well as a residual-based estimator with the best model choice-and some classical algorithms such as L-curve or elbow heuristics, Mallows' C p , and Akaike's FPE. Practical issues are also addressed, including two new practical definitions of minimal-penalty algorithms that are compared on synthetic data to previously-proposed definitions. Finally, several conjectures and open problems are suggested as future research directions.

Cross-validation

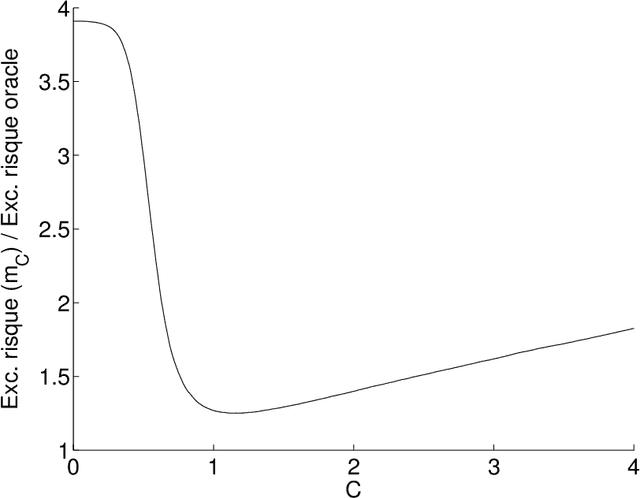
This text is a survey on cross-validation. We define all classical cross-validation procedures, and we study their properties for two different goals: estimating the risk of a given estimator, and selecting the best estimator among a given family. For the risk estimation problem, we compute the bias (which can also be corrected) and the variance of cross-validation methods. For estimator selection, we first provide a first-order analysis (based on expectations). Then, we explain how to take into account second-order terms (from variance computations, and by taking into account the usefulness of overpenalization). This allows, in the end, to provide some guidelines for choosing the best cross-validation method for a given learning problem.

Comments on: "A Random Forest Guided Tour" by G. Biau and E. Scornet

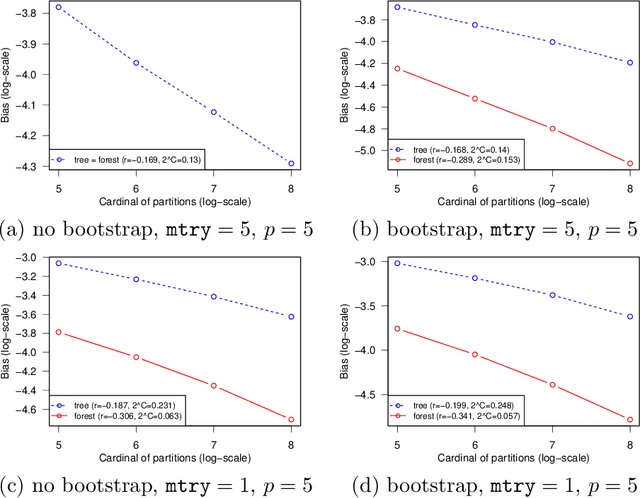
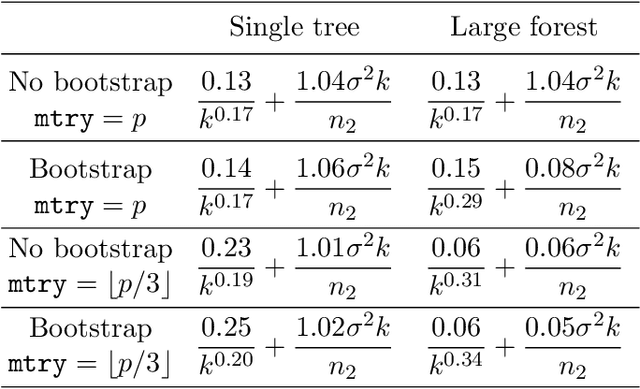
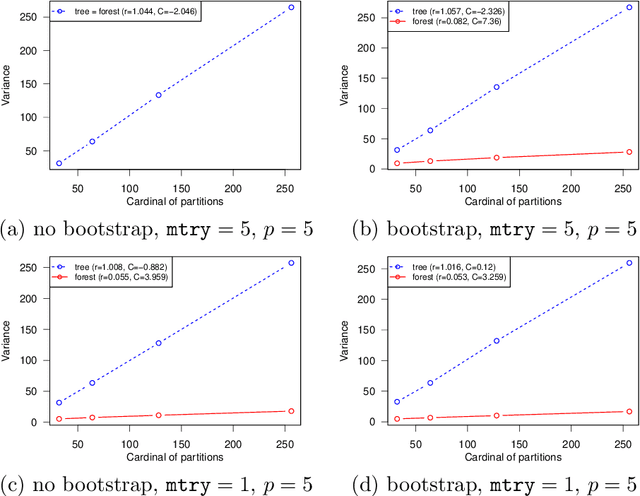
This paper is a comment on the survey paper by Biau and Scornet (2016) about random forests. We focus on the problem of quantifying the impact of each ingredient of random forests on their performance. We show that such a quantification is possible for a simple pure forest , leading to conclusions that could apply more generally. Then, we consider "hold-out" random forests, which are a good middle point between "toy" pure forests and Breiman's original random forests.

Choice of V for V-Fold Cross-Validation in Least-Squares Density Estimation

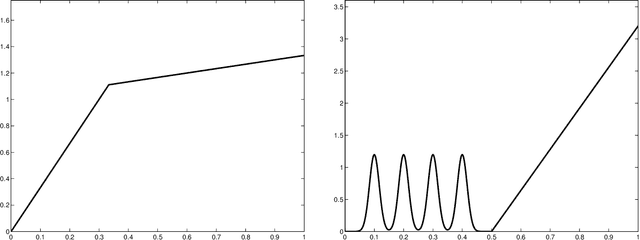
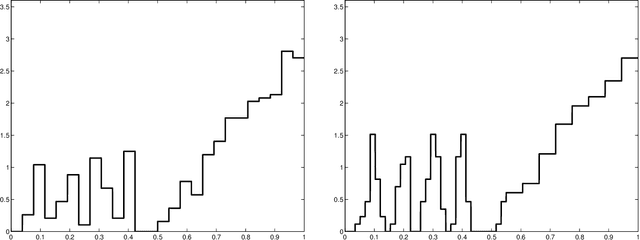
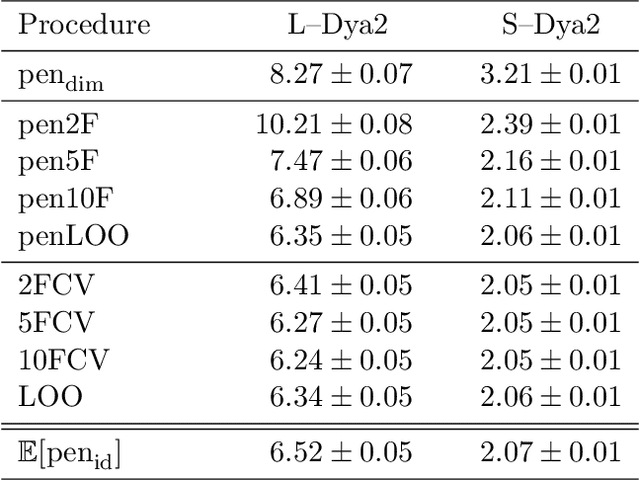
This paper studies V-fold cross-validation for model selection in least-squares density estimation. The goal is to provide theoretical grounds for choosing V in order to minimize the least-squares loss of the selected estimator. We first prove a non-asymptotic oracle inequality for V-fold cross-validation and its bias-corrected version (V-fold penalization). In particular, this result implies that V-fold penalization is asymptotically optimal in the nonparametric case. Then, we compute the variance of V-fold cross-validation and related criteria, as well as the variance of key quantities for model selection performance. We show that these variances depend on V like 1+4/(V-1), at least in some particular cases, suggesting that the performance increases much from V=2 to V=5 or 10, and then is almost constant. Overall, this can explain the common advice to take V=5---at least in our setting and when the computational power is limited---, as supported by some simulation experiments. An oracle inequality and exact formulas for the variance are also proved for Monte-Carlo cross-validation, also known as repeated cross-validation, where the parameter V is replaced by the number B of random splits of the data.