Random Forests for time-fixed and time-dependent predictors: The DynForest R package

The R package DynForest implements random forests for predicting a categorical or a (multiple causes) time-to-event outcome based on time-fixed and time-dependent predictors. Through the random forests, the time-dependent predictors can be measured with error at subject-specific times, and they can be endogeneous (i.e., impacted by the outcome process). They are modeled internally using flexible linear mixed models (thanks to lcmm package) with time-associations pre-specified by the user. DynForest computes dynamic predictions that take into account all the information from time-fixed and time-dependent predictors. DynForest also provides information about the most predictive variables using variable importance and minimal depth. Variable importance can also be computed on groups of variables. To display the results, several functions are available such as summary and plot functions. This paper aims to guide the user with a step-by-step example of the different functions for fitting random forests within DynForest.

Random survival forests for competing risks with multivariate longitudinal endogenous covariates

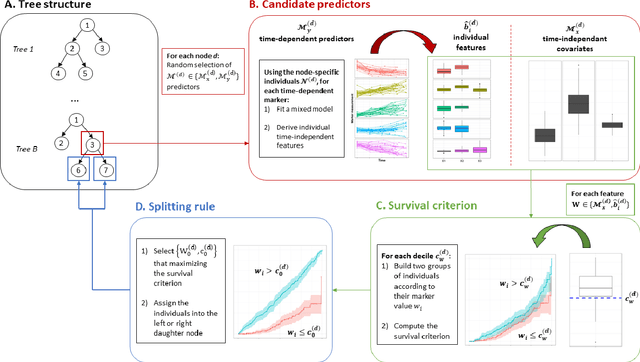
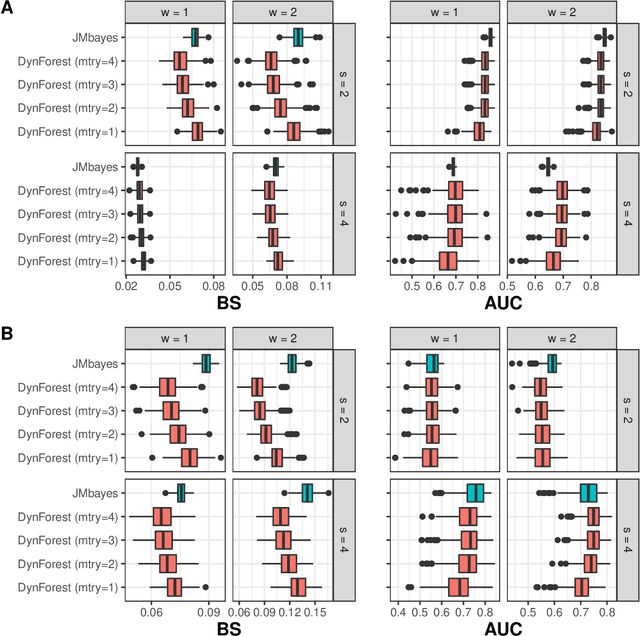
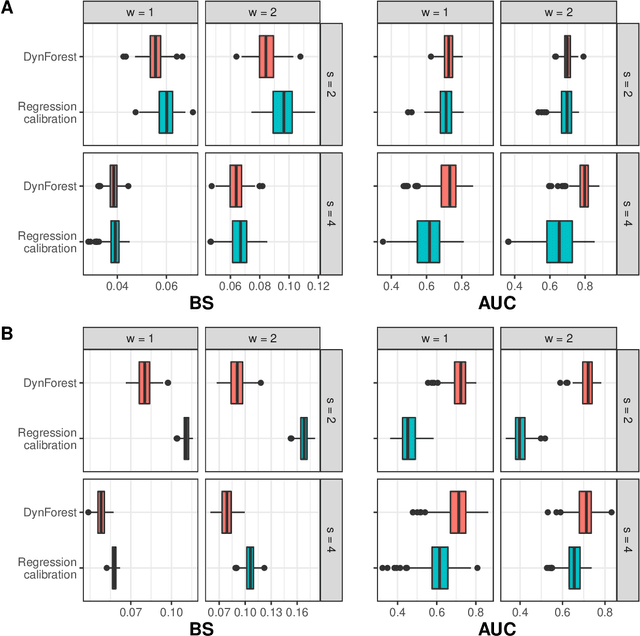
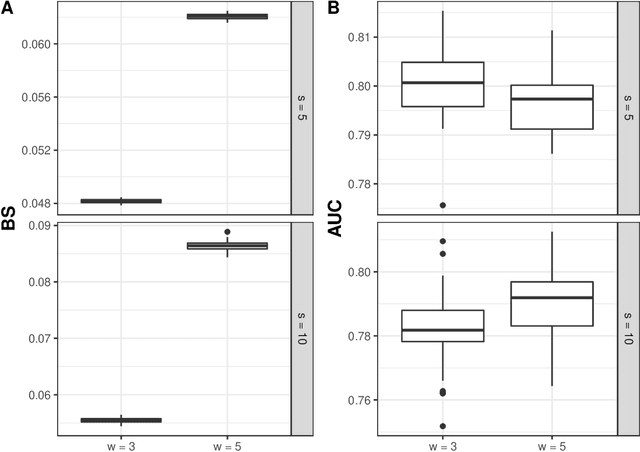
Predicting the individual risk of a clinical event using the complete patient history is still a major challenge for personalized medicine. Among the methods developed to compute individual dynamic predictions, the joint models have the assets of using all the available information while accounting for dropout. However, they are restricted to a very small number of longitudinal predictors. Our objective was to propose an innovative alternative solution to predict an event probability using a possibly large number of longitudinal predictors. We developed DynForest, an extension of random survival forests for competing risks that handles endogenous longitudinal predictors. At each node of the trees, the time-dependent predictors are translated into time-fixed features (using mixed models) to be used as candidates for splitting the subjects into two subgroups. The individual event probability is estimated in each tree by the Aalen-Johansen estimator of the leaf in which the subject is classified according to his/her history of predictors. The final individual prediction is given by the average of the tree-specific individual event probabilities. We carried out a simulation study to demonstrate the performances of DynForest both in a small dimensional context (in comparison with joint models) and in a large dimensional context (in comparison with a regression calibration method that ignores informative dropout). We also applied DynForest to (i) predict the individual probability of dementia in the elderly according to repeated measures of cognitive, functional, vascular and neuro-degeneration markers, and (ii) quantify the importance of each type of markers for the prediction of dementia. Implemented in the R package DynForest, our methodology provides a solution for the prediction of events from longitudinal endogenous predictors whatever their number.

Individual dynamic prediction of clinical endpoint from large dimensional longitudinal biomarker history: a landmark approach

The individual data collected throughout patient follow-up constitute crucial information for assessing the risk of a clinical event, and eventually for adapting a therapeutic strategy. Joint models and landmark models have been proposed to compute individual dynamic predictions from repeated measures to one or two markers. However, they hardly extend to the case where the complete patient history includes much more repeated markers possibly. Our objective was thus to propose a solution for the dynamic prediction of a health event that may exploit repeated measures of a possibly large number of markers. We combined a landmark approach extended to endogenous markers history with machine learning methods adapted to survival data. Each marker trajectory is modeled using the information collected up to landmark time, and summary variables that best capture the individual trajectories are derived. These summaries and additional covariates are then included in different prediction methods. To handle a possibly large dimensional history, we rely on machine learning methods adapted to survival data, namely regularized regressions and random survival forests, to predict the event from the landmark time, and we show how they can be combined into a superlearner. Then, the performances are evaluated by cross-validation using estimators of Brier Score and the area under the Receiver Operating Characteristic curve adapted to censored data. We demonstrate in a simulation study the benefits of machine learning survival methods over standard survival models, especially in the case of numerous and/or nonlinear relationships between the predictors and the event. We then applied the methodology in two prediction contexts: a clinical context with the prediction of death for patients with primary biliary cholangitis, and a public health context with the prediction of death in the general elderly population at different ages. Our methodology, implemented in R, enables the prediction of an event using the entire longitudinal patient history, even when the number of repeated markers is large. Although introduced with mixed models for the repeated markers and methods for a single right censored time-to-event, our method can be used with any other appropriate modeling technique for the markers and can be easily extended to competing risks setting.

Fréchet random forests

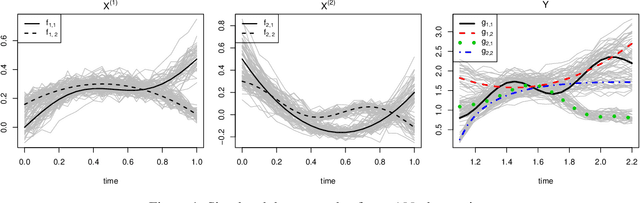
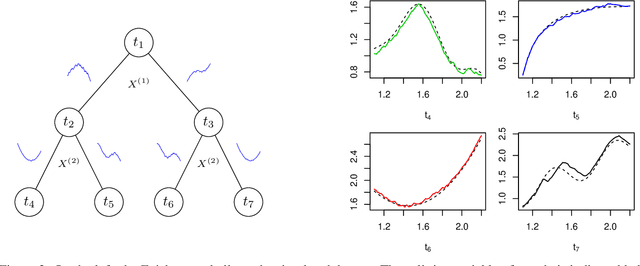
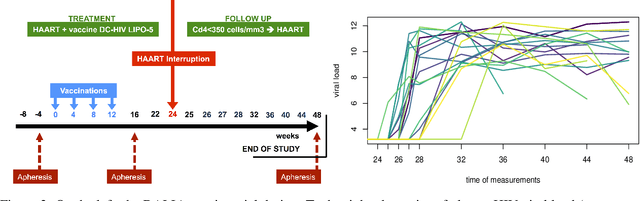
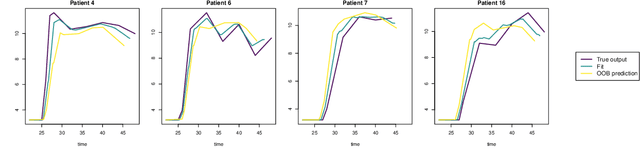
Random forests are a statistical learning method widely used in many areas of scientific research essentially for its ability to learn complex relationship between input and output variables and also its capacity to handle high-dimensional data. However, data are increasingly complex with repeated measures of omics, images leading to shapes, curves... Random forests method is not specifically tailored for them. In this paper, we introduce Fr\'echet trees and Fr\'echet random forests, which allow to manage data for which input and output variables take values in general metric spaces (which can be unordered). To this end, a new way of splitting the nodes of trees is introduced and the prediction procedures of trees and forests are generalized. Then, random forests out-of-bag error and variable importance score are naturally adapted. Finally, the method is studied in the special case of regression on curve shapes, both within a simulation study and a real dataset from an HIV vaccine trial.

Random Forests for Big Data

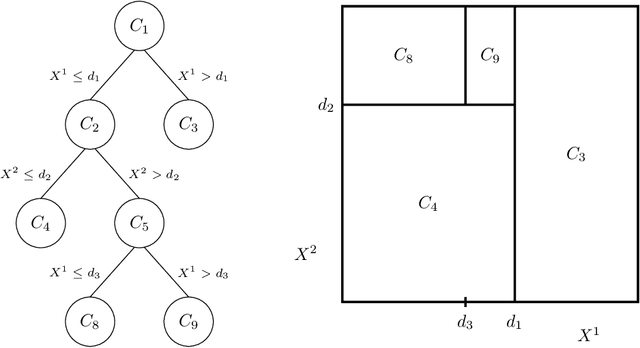
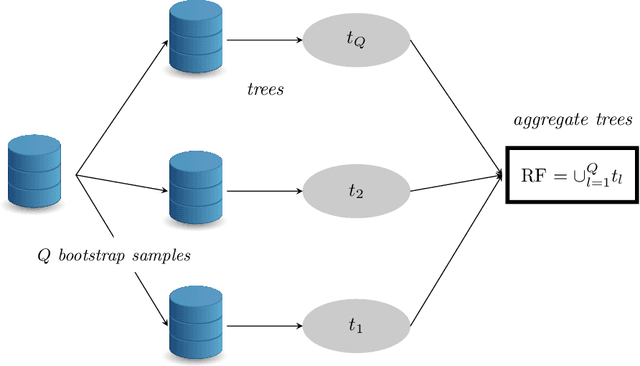
Big Data is one of the major challenges of statistical science and has numerous consequences from algorithmic and theoretical viewpoints. Big Data always involve massive data but they also often include online data and data heterogeneity. Recently some statistical methods have been adapted to process Big Data, like linear regression models, clustering methods and bootstrapping schemes. Based on decision trees combined with aggregation and bootstrap ideas, random forests were introduced by Breiman in 2001. They are a powerful nonparametric statistical method allowing to consider in a single and versatile framework regression problems, as well as two-class and multi-class classification problems. Focusing on classification problems, this paper proposes a selective review of available proposals that deal with scaling random forests to Big Data problems. These proposals rely on parallel environments or on online adaptations of random forests. We also describe how related quantities -- such as out-of-bag error and variable importance -- are addressed in these methods. Then, we formulate various remarks for random forests in the Big Data context. Finally, we experiment five variants on two massive datasets (15 and 120 millions of observations), a simulated one as well as real world data. One variant relies on subsampling while three others are related to parallel implementations of random forests and involve either various adaptations of bootstrap to Big Data or to "divide-and-conquer" approaches. The fifth variant relates on online learning of random forests. These numerical experiments lead to highlight the relative performance of the different variants, as well as some of their limitations.

Comments on: "A Random Forest Guided Tour" by G. Biau and E. Scornet

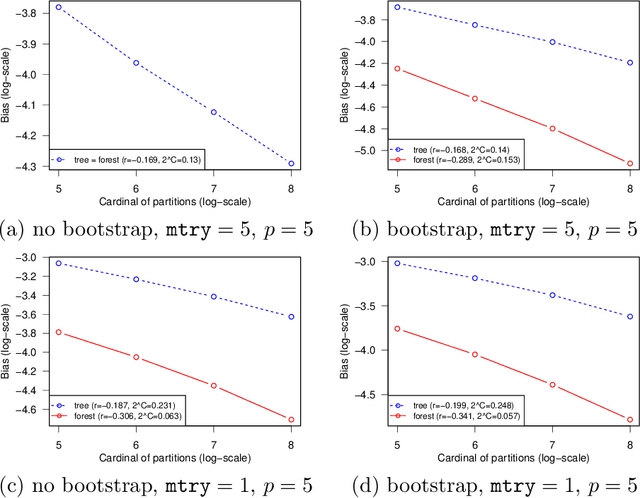
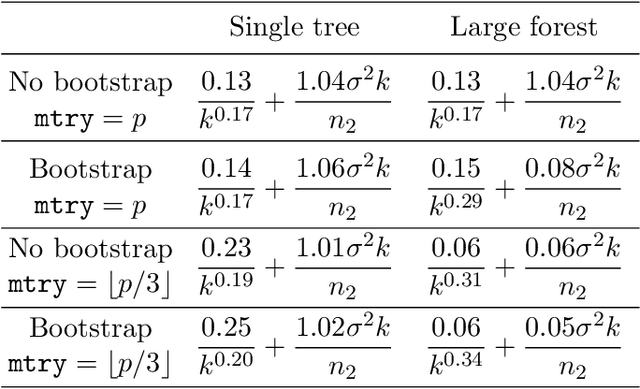
This paper is a comment on the survey paper by Biau and Scornet (2016) about random forests. We focus on the problem of quantifying the impact of each ingredient of random forests on their performance. We show that such a quantification is possible for a simple pure forest , leading to conclusions that could apply more generally. Then, we consider "hold-out" random forests, which are a good middle point between "toy" pure forests and Breiman's original random forests.

Analysis of purely random forests bias

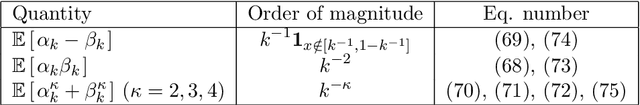
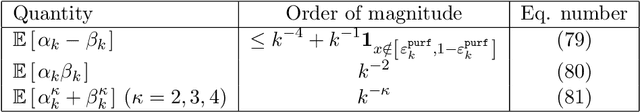
Random forests are a very effective and commonly used statistical method, but their full theoretical analysis is still an open problem. As a first step, simplified models such as purely random forests have been introduced, in order to shed light on the good performance of random forests. In this paper, we study the approximation error (the bias) of some purely random forest models in a regression framework, focusing in particular on the influence of the number of trees in the forest. Under some regularity assumptions on the regression function, we show that the bias of an infinite forest decreases at a faster rate (with respect to the size of each tree) than a single tree. As a consequence, infinite forests attain a strictly better risk rate (with respect to the sample size) than single trees. Furthermore, our results allow to derive a minimum number of trees sufficient to reach the same rate as an infinite forest. As a by-product of our analysis, we also show a link between the bias of purely random forests and the bias of some kernel estimators.

Random Forests: some methodological insights

This paper examines from an experimental perspective random forests, the increasingly used statistical method for classification and regression problems introduced by Leo Breiman in 2001. It first aims at confirming, known but sparse, advice for using random forests and at proposing some complementary remarks for both standard problems as well as high dimensional ones for which the number of variables hugely exceeds the sample size. But the main contribution of this paper is twofold: to provide some insights about the behavior of the variable importance index based on random forests and in addition, to propose to investigate two classical issues of variable selection. The first one is to find important variables for interpretation and the second one is more restrictive and try to design a good prediction model. The strategy involves a ranking of explanatory variables using the random forests score of importance and a stepwise ascending variable introduction strategy.