EpidemiOptim: A Toolbox for the Optimization of Control Policies in Epidemiological Models

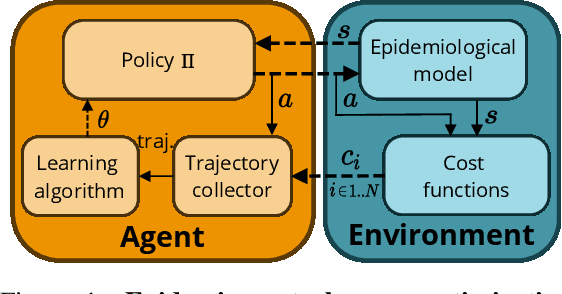
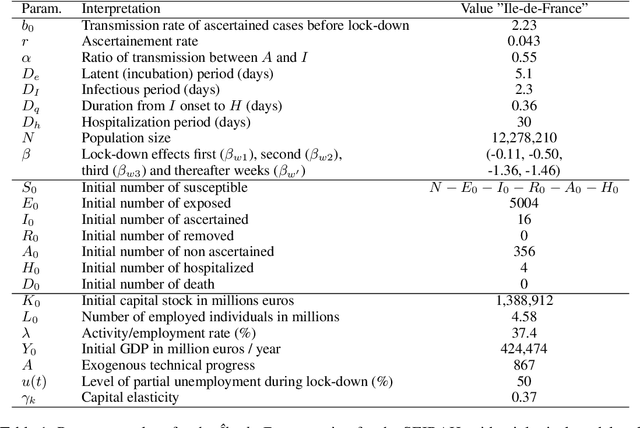
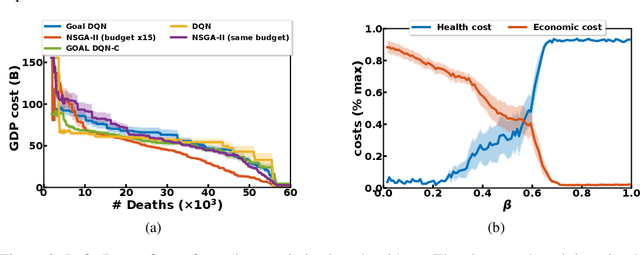
Epidemiologists model the dynamics of epidemics in order to propose control strategies based on pharmaceutical and non-pharmaceutical interventions (contact limitation, lock down, vaccination, etc). Hand-designing such strategies is not trivial because of the number of possible interventions and the difficulty to predict long-term effects. This task can be cast as an optimization problem where state-of-the-art machine learning algorithms such as deep reinforcement learning, might bring significant value. However, the specificity of each domain -- epidemic modelling or solving optimization problem -- requires strong collaborations between researchers from different fields of expertise. This is why we introduce EpidemiOptim, a Python toolbox that facilitates collaborations between researchers in epidemiology and optimization. EpidemiOptim turns epidemiological models and cost functions into optimization problems via a standard interface commonly used by optimization practitioners (OpenAI Gym). Reinforcement learning algorithms based on Q-Learning with deep neural networks (DQN) and evolutionary algorithms (NSGA-II) are already implemented. We illustrate the use of EpidemiOptim to find optimal policies for dynamical on-off lock-down control under the optimization of death toll and economic recess using a Susceptible-Exposed-Infectious-Removed (SEIR) model for COVID-19. Using EpidemiOptim and its interactive visualization platform in Jupyter notebooks, epidemiologists, optimization practitioners and others (e.g. economists) can easily compare epidemiological models, costs functions and optimization algorithms to address important choices to be made by health decision-makers.

Fréchet random forests

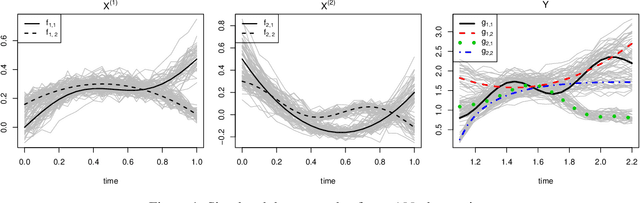
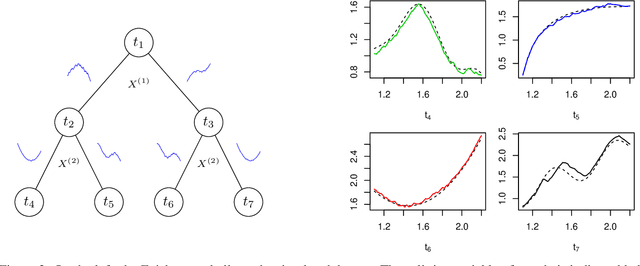
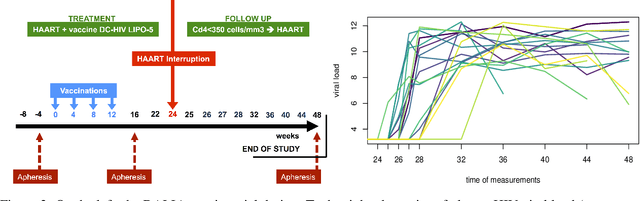
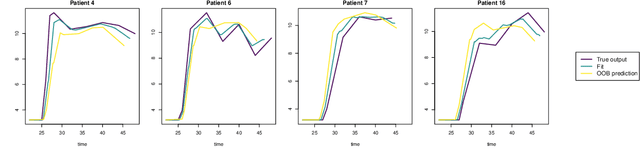
Random forests are a statistical learning method widely used in many areas of scientific research essentially for its ability to learn complex relationship between input and output variables and also its capacity to handle high-dimensional data. However, data are increasingly complex with repeated measures of omics, images leading to shapes, curves... Random forests method is not specifically tailored for them. In this paper, we introduce Fr\'echet trees and Fr\'echet random forests, which allow to manage data for which input and output variables take values in general metric spaces (which can be unordered). To this end, a new way of splitting the nodes of trees is introduced and the prediction procedures of trees and forests are generalized. Then, random forests out-of-bag error and variable importance score are naturally adapted. Finally, the method is studied in the special case of regression on curve shapes, both within a simulation study and a real dataset from an HIV vaccine trial.

Supervised Learning for Multi-Block Incomplete Data

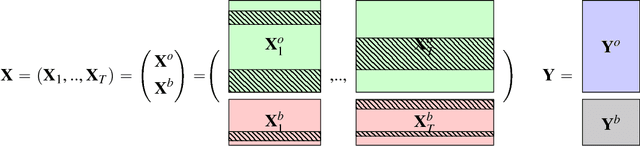
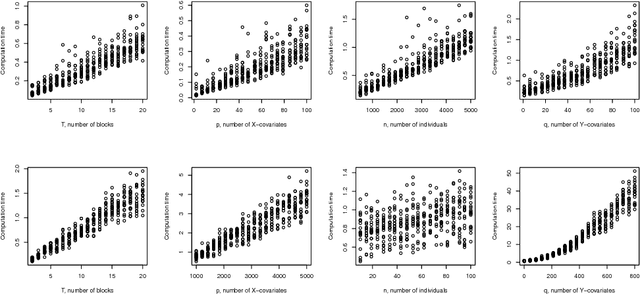
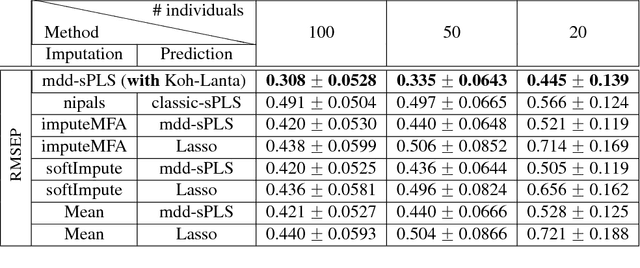
In the supervised high dimensional settings with a large number of variables and a low number of individuals, one objective is to select the relevant variables and thus to reduce the dimension. That subspace selection is often managed with supervised tools. However, some data can be missing, compromising the validity of the sub-space selection. We propose a Partial Least Square (PLS) based method, called Multi-block Data-Driven sparse PLS mdd-sPLS, allowing jointly variable selection and subspace estimation while training and testing missing data imputation through a new algorithm called Koh-Lanta. This method was challenged through simulations against existing methods such as mean imputation, nipals, softImpute and imputeMFA. In the context of supervised analysis of high dimensional data, the proposed method shows the lowest prediction error of the response variables. So far this is the only method combining data imputation and response variable prediction. The superiority of the supervised multi-block mdd-sPLS method increases with the intra-block and inter-block correlations. The application to a real data-set from a rVSV-ZEBOV Ebola vaccine trial revealed interesting and biologically relevant results. The method is implemented in a R-package available on the CRAN and a Python-package available on pypi.

Sequential Dirichlet Process Mixtures of Multivariate Skew t-distributions for Model-based Clustering of Flow Cytometry Data

Flow cytometry is a high-throughput technology used to quantify multiple surface and intracellular markers at the level of a single cell. This enables to identify cell sub-types, and to determine their relative proportions. Improvements of this technology allow to describe millions of individual cells from a blood sample using multiple markers. This results in high-dimensional datasets, whose manual analysis is highly time-consuming and poorly reproducible. While several methods have been developed to perform automatic recognition of cell populations, most of them treat and analyze each sample independently. However, in practice, individual samples are rarely independent (e.g. longitudinal studies). Here, we propose to use a Bayesian nonparametric approach with Dirichlet process mixture (DPM) of multivariate skew $t$-distributions to perform model based clustering of flow-cytometry data. DPM models directly estimate the number of cell populations from the data, avoiding model selection issues, and skew $t$-distributions provides robustness to outliers and non-elliptical shape of cell populations. To accommodate repeated measurements, we propose a sequential strategy relying on a parametric approximation of the posterior. We illustrate the good performance of our method on simulated data, on an experimental benchmark dataset, and on new longitudinal data from the DALIA-1 trial which evaluates a therapeutic vaccine against HIV. On the benchmark dataset, the sequential strategy outperforms all other methods evaluated, and similarly, leads to improved performance on the DALIA-1 data. We have made the method available for the community in the R package NPflow.