On the potential benefits of entropic regularization for smoothing Wasserstein estimators

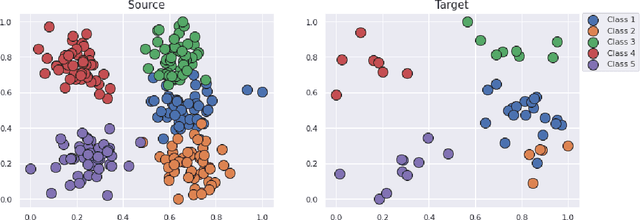
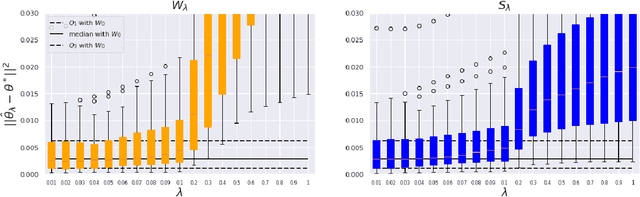
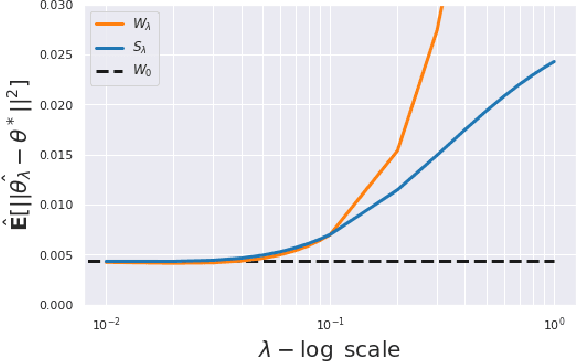
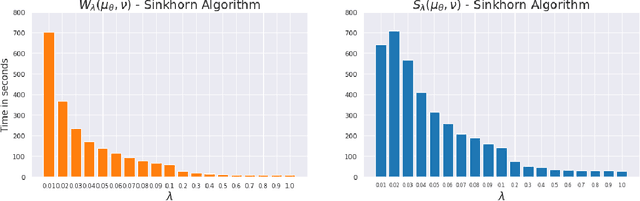
This paper is focused on the study of entropic regularization in optimal transport as a smoothing method for Wasserstein estimators, through the prism of the classical tradeoff between approximation and estimation errors in statistics. Wasserstein estimators are defined as solutions of variational problems whose objective function involves the use of an optimal transport cost between probability measures. Such estimators can be regularized by replacing the optimal transport cost by its regularized version using an entropy penalty on the transport plan. The use of such a regularization has a potentially significant smoothing effect on the resulting estimators. In this work, we investigate its potential benefits on the approximation and estimation properties of regularized Wasserstein estimators. Our main contribution is to discuss how entropic regularization may reach, at a lowest computational cost, statistical performances that are comparable to those of un-regularized Wasserstein estimators in statistical learning problems involving distributional data analysis. To this end, we present new theoretical results on the convergence of regularized Wasserstein estimators. We also study their numerical performances using simulated and real data in the supervised learning problem of proportions estimation in mixture models using optimal transport.

Sequential Dirichlet Process Mixtures of Multivariate Skew t-distributions for Model-based Clustering of Flow Cytometry Data

Flow cytometry is a high-throughput technology used to quantify multiple surface and intracellular markers at the level of a single cell. This enables to identify cell sub-types, and to determine their relative proportions. Improvements of this technology allow to describe millions of individual cells from a blood sample using multiple markers. This results in high-dimensional datasets, whose manual analysis is highly time-consuming and poorly reproducible. While several methods have been developed to perform automatic recognition of cell populations, most of them treat and analyze each sample independently. However, in practice, individual samples are rarely independent (e.g. longitudinal studies). Here, we propose to use a Bayesian nonparametric approach with Dirichlet process mixture (DPM) of multivariate skew $t$-distributions to perform model based clustering of flow-cytometry data. DPM models directly estimate the number of cell populations from the data, avoiding model selection issues, and skew $t$-distributions provides robustness to outliers and non-elliptical shape of cell populations. To accommodate repeated measurements, we propose a sequential strategy relying on a parametric approximation of the posterior. We illustrate the good performance of our method on simulated data, on an experimental benchmark dataset, and on new longitudinal data from the DALIA-1 trial which evaluates a therapeutic vaccine against HIV. On the benchmark dataset, the sequential strategy outperforms all other methods evaluated, and similarly, leads to improved performance on the DALIA-1 data. We have made the method available for the community in the R package NPflow.