Equivariant Denoisers for Plug and Play Image Restoration

One key ingredient of image restoration is to define a realistic prior on clean images to complete the missing information in the observation. State-of-the-art restoration methods rely on a neural network to encode this prior. Typical image distributions are invariant to some set of transformations, such as rotations or flips. However, most deep architectures are not designed to represent an invariant image distribution. Recent works have proposed to overcome this difficulty by including equivariance properties within a Plug-and-Play paradigm. In this work, we propose two unified frameworks named Equivariant Regularization by Denoising (ERED) and Equivariant Plug-and-Play (EPnP) based on equivariant denoisers and stochastic optimization. We analyze the convergence of the proposed algorithms and discuss their practical benefit.

From stability of Langevin diffusion to convergence of proximal MCMC for non-log-concave sampling

We consider the problem of sampling distributions stemming from non-convex potentials with Unadjusted Langevin Algorithm (ULA). We prove the stability of the discrete-time ULA to drift approximations under the assumption that the potential is strongly convex at infinity. In many context, e.g. imaging inverse problems, potentials are non-convex and non-smooth. Proximal Stochastic Gradient Langevin Algorithm (PSGLA) is a popular algorithm to handle such potentials. It combines the forward-backward optimization algorithm with a ULA step. Our main stability result combined with properties of the Moreau envelope allows us to derive the first proof of convergence of the PSGLA for non-convex potentials. We empirically validate our methodology on synthetic data and in the context of imaging inverse problems. In particular, we observe that PSGLA exhibits faster convergence rates than Stochastic Gradient Langevin Algorithm for posterior sampling while preserving its restoration properties.

Equivariant Denoisers for Image Restoration

One key ingredient of image restoration is to define a realistic prior on clean images to complete the missing information in the observation. State-of-the-art restoration methods rely on a neural network to encode this prior. Moreover, typical image distributions are invariant to some set of transformations, such as rotations or flips. However, most deep architectures are not designed to represent an invariant image distribution. Recent works have proposed to overcome this difficulty by including equivariance properties within a Plug-and-Play paradigm. In this work, we propose a unified framework named Equivariant Regularization by Denoising (ERED) based on equivariant denoisers and stochastic optimization. We analyze the convergence of this algorithm and discuss its practical benefit.

Plug-and-Play image restoration with Stochastic deNOising REgularization

Plug-and-Play (PnP) algorithms are a class of iterative algorithms that address image inverse problems by combining a physical model and a deep neural network for regularization. Even if they produce impressive image restoration results, these algorithms rely on a non-standard use of a denoiser on images that are less and less noisy along the iterations, which contrasts with recent algorithms based on Diffusion Models (DM), where the denoiser is applied only on re-noised images. We propose a new PnP framework, called Stochastic deNOising REgularization (SNORE), which applies the denoiser only on images with noise of the adequate level. It is based on an explicit stochastic regularization, which leads to a stochastic gradient descent algorithm to solve ill-posed inverse problems. A convergence analysis of this algorithm and its annealing extension is provided. Experimentally, we prove that SNORE is competitive with respect to state-of-the-art methods on deblurring and inpainting tasks, both quantitatively and qualitatively.

Convergent plug-and-play with proximal denoiser and unconstrained regularization parameter

In this work, we present new proofs of convergence for Plug-and-Play (PnP) algorithms. PnP methods are efficient iterative algorithms for solving image inverse problems where regularization is performed by plugging a pre-trained denoiser in a proximal algorithm, such as Proximal Gradient Descent (PGD) or Douglas-Rachford Splitting (DRS). Recent research has explored convergence by incorporating a denoiser that writes exactly as a proximal operator. However, the corresponding PnP algorithm has then to be run with stepsize equal to $1$. The stepsize condition for nonconvex convergence of the proximal algorithm in use then translates to restrictive conditions on the regularization parameter of the inverse problem. This can severely degrade the restoration capacity of the algorithm. In this paper, we present two remedies for this limitation. First, we provide a novel convergence proof for PnP-DRS that does not impose any restrictions on the regularization parameter. Second, we examine a relaxed version of the PGD algorithm that converges across a broader range of regularization parameters. Our experimental study, conducted on deblurring and super-resolution experiments, demonstrate that both of these solutions enhance the accuracy of image restoration.

Convergent Bregman Plug-and-Play Image Restoration for Poisson Inverse Problems

Plug-and-Play (PnP) methods are efficient iterative algorithms for solving ill-posed image inverse problems. PnP methods are obtained by using deep Gaussian denoisers instead of the proximal operator or the gradient-descent step within proximal algorithms. Current PnP schemes rely on data-fidelity terms that have either Lipschitz gradients or closed-form proximal operators, which is not applicable to Poisson inverse problems. Based on the observation that the Gaussian noise is not the adequate noise model in this setting, we propose to generalize PnP using theBregman Proximal Gradient (BPG) method. BPG replaces the Euclidean distance with a Bregman divergence that can better capture the smoothness properties of the problem. We introduce the Bregman Score Denoiser specifically parametrized and trained for the new Bregman geometry and prove that it corresponds to the proximal operator of a nonconvex potential. We propose two PnP algorithms based on the Bregman Score Denoiser for solving Poisson inverse problems. Extending the convergence results of BPG in the nonconvex settings, we show that the proposed methods converge, targeting stationary points of an explicit global functional. Experimental evaluations conducted on various Poisson inverse problems validate the convergence results and showcase effective restoration performance.

A relaxed proximal gradient descent algorithm for convergent plug-and-play with proximal denoiser

This paper presents a new convergent Plug-and-Play (PnP) algorithm. PnP methods are efficient iterative algorithms for solving image inverse problems formulated as the minimization of the sum of a data-fidelity term and a regularization term. PnP methods perform regularization by plugging a pre-trained denoiser in a proximal algorithm, such as Proximal Gradient Descent (PGD). To ensure convergence of PnP schemes, many works study specific parametrizations of deep denoisers. However, existing results require either unverifiable or suboptimal hypotheses on the denoiser, or assume restrictive conditions on the parameters of the inverse problem. Observing that these limitations can be due to the proximal algorithm in use, we study a relaxed version of the PGD algorithm for minimizing the sum of a convex function and a weakly convex one. When plugged with a relaxed proximal denoiser, we show that the proposed PnP-$\alpha$PGD algorithm converges for a wider range of regularization parameters, thus allowing more accurate image restoration.

On the potential benefits of entropic regularization for smoothing Wasserstein estimators

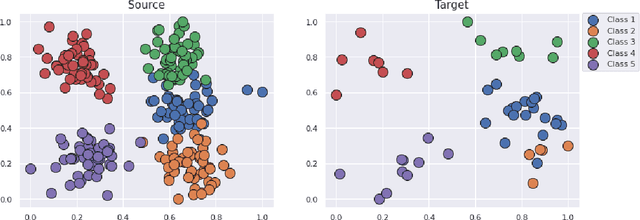
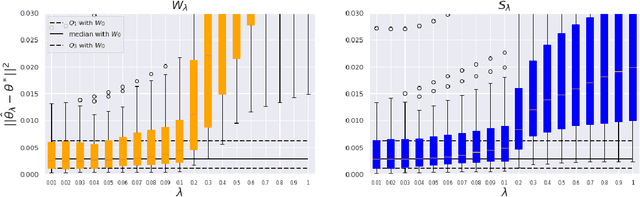
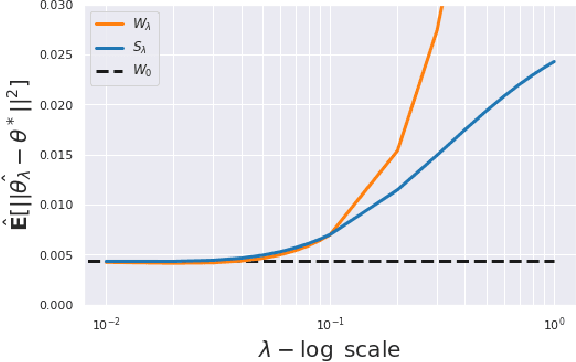
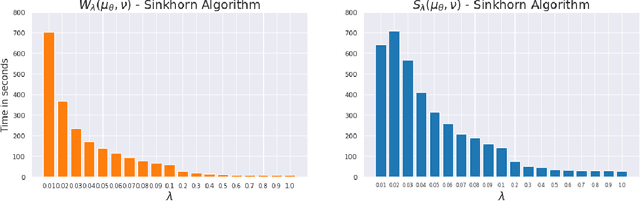
This paper is focused on the study of entropic regularization in optimal transport as a smoothing method for Wasserstein estimators, through the prism of the classical tradeoff between approximation and estimation errors in statistics. Wasserstein estimators are defined as solutions of variational problems whose objective function involves the use of an optimal transport cost between probability measures. Such estimators can be regularized by replacing the optimal transport cost by its regularized version using an entropy penalty on the transport plan. The use of such a regularization has a potentially significant smoothing effect on the resulting estimators. In this work, we investigate its potential benefits on the approximation and estimation properties of regularized Wasserstein estimators. Our main contribution is to discuss how entropic regularization may reach, at a lowest computational cost, statistical performances that are comparable to those of un-regularized Wasserstein estimators in statistical learning problems involving distributional data analysis. To this end, we present new theoretical results on the convergence of regularized Wasserstein estimators. We also study their numerical performances using simulated and real data in the supervised learning problem of proportions estimation in mixture models using optimal transport.

Proximal denoiser for convergent plug-and-play optimization with nonconvex regularization

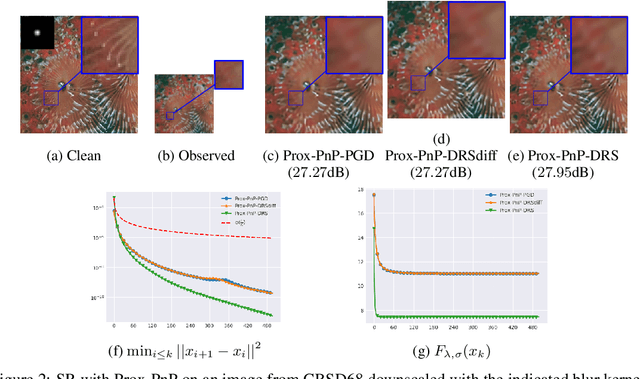
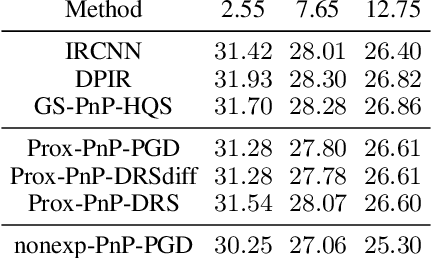
Plug-and-Play (PnP) methods solve ill-posed inverse problems through iterative proximal algorithms by replacing a proximal operator by a denoising operation. When applied with deep neural network denoisers, these methods have shown state-of-the-art visual performance for image restoration problems. However, their theoretical convergence analysis is still incomplete. Most of the existing convergence results consider nonexpansive denoisers, which is non-realistic, or limit their analysis to strongly convex data-fidelity terms in the inverse problem to solve. Recently, it was proposed to train the denoiser as a gradient descent step on a functional parameterized by a deep neural network. Using such a denoiser guarantees the convergence of the PnP version of the Half-Quadratic-Splitting (PnP-HQS) iterative algorithm. In this paper, we show that this gradient denoiser can actually correspond to the proximal operator of another scalar function. Given this new result, we exploit the convergence theory of proximal algorithms in the nonconvex setting to obtain convergence results for PnP-PGD (Proximal Gradient Descent) and PnP-ADMM (Alternating Direction Method of Multipliers). When built on top of a smooth gradient denoiser, we show that PnP-PGD and PnP-ADMM are convergent and target stationary points of an explicit functional. These convergence results are confirmed with numerical experiments on deblurring, super-resolution and inpainting.

Gradient Step Denoiser for convergent Plug-and-Play

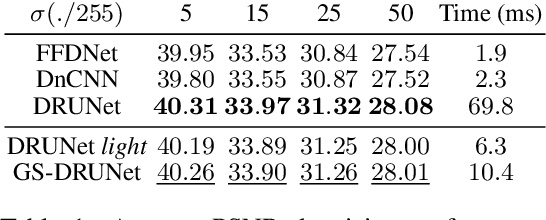
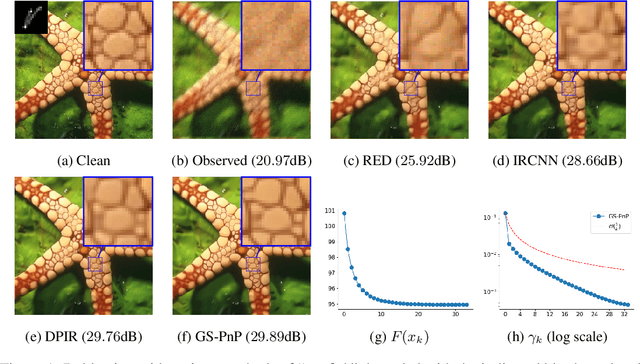
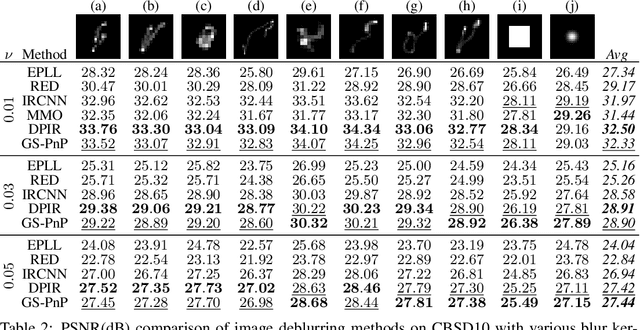
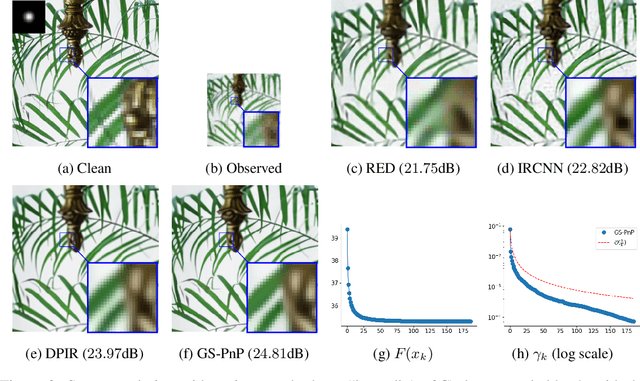
Plug-and-Play methods constitute a class of iterative algorithms for imaging problems where regularization is performed by an off-the-shelf denoiser. Although Plug-and-Play methods can lead to tremendous visual performance for various image problems, the few existing convergence guarantees are based on unrealistic (or suboptimal) hypotheses on the denoiser, or limited to strongly convex data terms. In this work, we propose a new type of Plug-and-Play methods, based on half-quadratic splitting, for which the denoiser is realized as a gradient descent step on a functional parameterized by a deep neural network. Exploiting convergence results for proximal gradient descent algorithms in the non-convex setting, we show that the proposed Plug-and-Play algorithm is a convergent iterative scheme that targets stationary points of an explicit global functional. Besides, experiments show that it is possible to learn such a deep denoiser while not compromising the performance in comparison to other state-of-the-art deep denoisers used in Plug-and-Play schemes. We apply our proximal gradient algorithm to various ill-posed inverse problems, e.g. deblurring, super-resolution and inpainting. For all these applications, numerical results empirically confirm the convergence results. Experiments also show that this new algorithm reaches state-of-the-art performance, both quantitatively and qualitatively.