Convergent Bregman Plug-and-Play Image Restoration for Poisson Inverse Problems

Plug-and-Play (PnP) methods are efficient iterative algorithms for solving ill-posed image inverse problems. PnP methods are obtained by using deep Gaussian denoisers instead of the proximal operator or the gradient-descent step within proximal algorithms. Current PnP schemes rely on data-fidelity terms that have either Lipschitz gradients or closed-form proximal operators, which is not applicable to Poisson inverse problems. Based on the observation that the Gaussian noise is not the adequate noise model in this setting, we propose to generalize PnP using theBregman Proximal Gradient (BPG) method. BPG replaces the Euclidean distance with a Bregman divergence that can better capture the smoothness properties of the problem. We introduce the Bregman Score Denoiser specifically parametrized and trained for the new Bregman geometry and prove that it corresponds to the proximal operator of a nonconvex potential. We propose two PnP algorithms based on the Bregman Score Denoiser for solving Poisson inverse problems. Extending the convergence results of BPG in the nonconvex settings, we show that the proposed methods converge, targeting stationary points of an explicit global functional. Experimental evaluations conducted on various Poisson inverse problems validate the convergence results and showcase effective restoration performance.

Coordinate-Based Seismic Interpolation in Irregular Land Survey: A Deep Internal Learning Approach

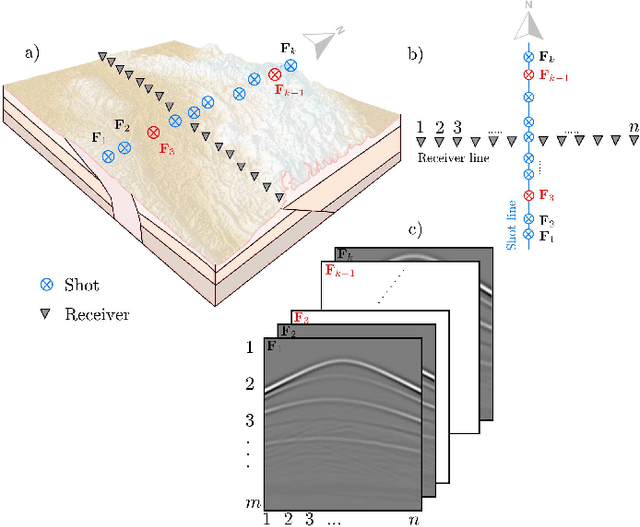
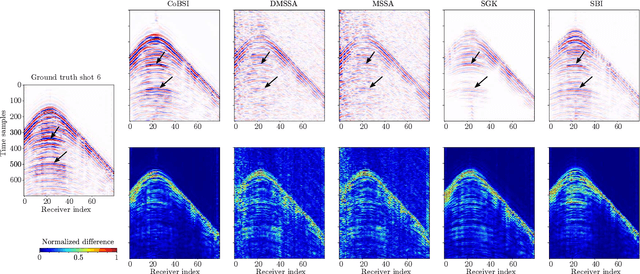
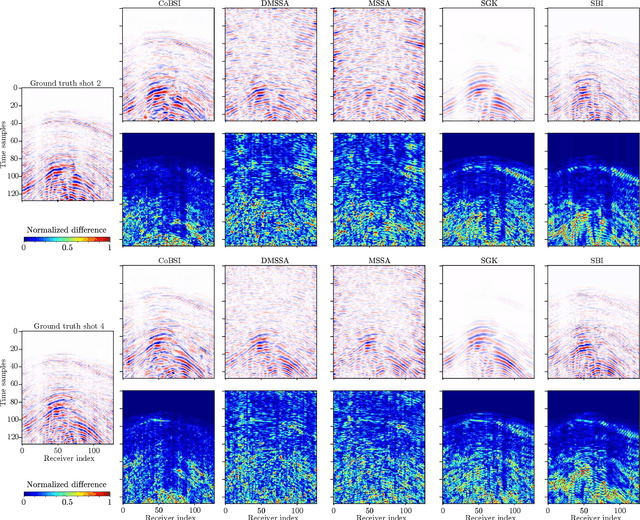
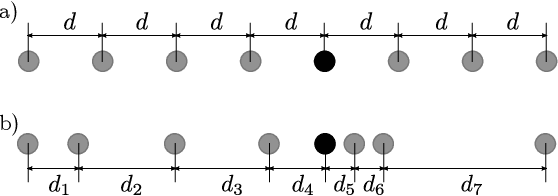
Physical and budget constraints often result in irregular sampling, which complicates accurate subsurface imaging. Pre-processing approaches, such as missing trace or shot interpolation, are typically employed to enhance seismic data in such cases. Recently, deep learning has been used to address the trace interpolation problem at the expense of large amounts of training data to adequately represent typical seismic events. Nonetheless, state-of-the-art works have mainly focused on trace reconstruction, with little attention having been devoted to shot interpolation. Furthermore, existing methods assume regularly spaced receivers/sources failing in approximating seismic data from real (irregular) surveys. This work presents a novel shot gather interpolation approach which uses a continuous coordinate-based representation of the acquired seismic wavefield parameterized by a neural network. The proposed unsupervised approach, which we call coordinate-based seismic interpolation (CoBSI), enables the prediction of specific seismic characteristics in irregular land surveys without using external data during neural network training. Experimental results on real and synthetic 3D data validate the ability of the proposed method to estimate continuous smooth seismic events in the time-space and frequency-wavenumber domains, improving sparsity or low rank-based interpolation methods.

Zero-Shot Learning of Continuous 3D Refractive Index Maps from Discrete Intensity-Only Measurements

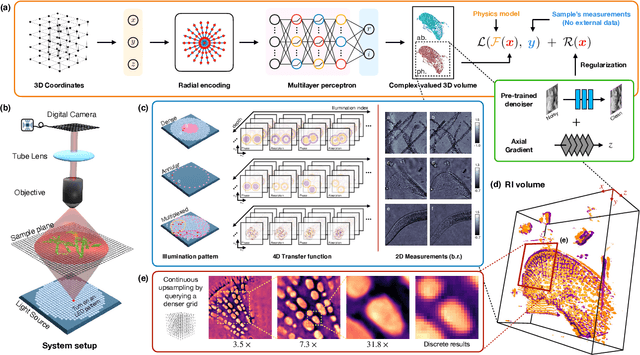
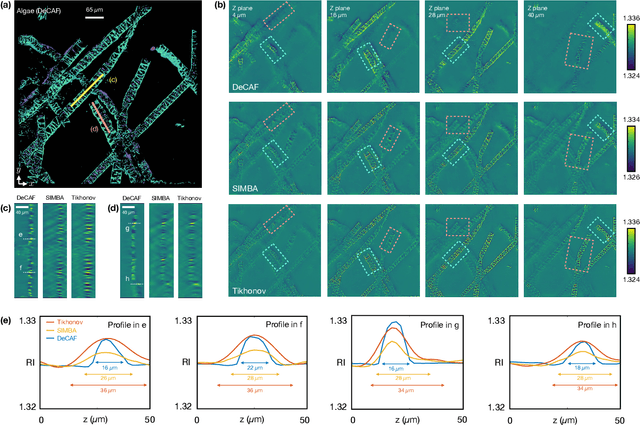
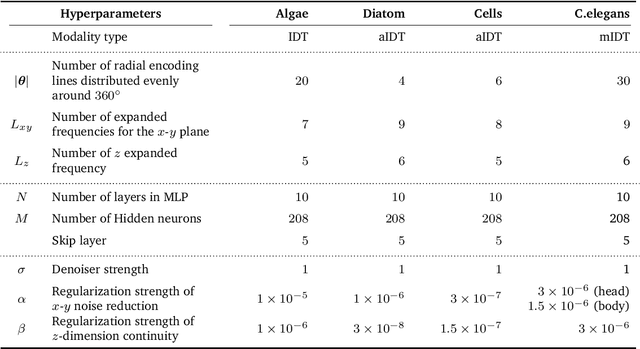
Intensity diffraction tomography (IDT) refers to a class of optical microscopy techniques for imaging the 3D refractive index (RI) distribution of a sample from a set of 2D intensity-only measurements. The reconstruction of artifact-free RI maps is a fundamental challenge in IDT due to the loss of phase information and the missing cone problem. Neural fields (NF) has recently emerged as a new deep learning (DL) paradigm for learning continuous representations of complex 3D scenes without external training datasets. We present DeCAF as the first NF-based IDT method that can learn a high-quality continuous representation of a RI volume directly from its intensity-only and limited-angle measurements. We show on three different IDT modalities and multiple biological samples that DeCAF can generate high-contrast and artifact-free RI maps.