Edwin Vargas
NOWA: Null-space Optical Watermark for Invisible Capture Fingerprinting and Tamper Localization
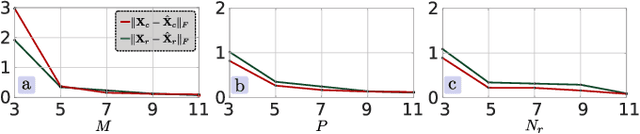
Dec 27, 2025Abstract:Ensuring the authenticity and ownership of digital images is increasingly challenging as modern editing tools enable highly realistic forgeries. Existing image protection systems mainly rely on digital watermarking, which is susceptible to sophisticated digital attacks. To address this limitation, we propose a hybrid optical-digital framework that incorporates physical authentication cues during image formation and preserves them through a learned reconstruction process. At the optical level, a phase mask in the camera aperture produces a Null-space Optical Watermark (NOWA) that lies in the Null Space of the imaging operator and therefore remains invisible in the captured image. Then, a Null-Space Network (NSN) performs measurement-consistent reconstruction that delivers high-quality protected images while preserving the NOWA signature. The proposed design enables tamper localization by projecting the image onto the camera's null space and detecting pixel-level inconsistencies. Our design preserves perceptual quality, resists common degradations such as compression, and establishes a structural security asymmetry: without access to the optical or NSN parameters, adversaries cannot forge the NOWA signature. Experiments with simulations and a prototype camera demonstrate competitive performance in terms of image quality preservation, and tamper localization accuracy compared to state-of-the-art digital watermarking and learning-based authentication methods.
BiPer: Binary Neural Networks using a Periodic Function
Apr 01, 2024Abstract:Quantized neural networks employ reduced precision representations for both weights and activations. This quantization process significantly reduces the memory requirements and computational complexity of the network. Binary Neural Networks (BNNs) are the extreme quantization case, representing values with just one bit. Since the sign function is typically used to map real values to binary values, smooth approximations are introduced to mimic the gradients during error backpropagation. Thus, the mismatch between the forward and backward models corrupts the direction of the gradient, causing training inconsistency problems and performance degradation. In contrast to current BNN approaches, we propose to employ a binary periodic (BiPer) function during binarization. Specifically, we use a square wave for the forward pass to obtain the binary values and employ the trigonometric sine function with the same period of the square wave as a differentiable surrogate during the backward pass. We demonstrate that this approach can control the quantization error by using the frequency of the periodic function and improves network performance. Extensive experiments validate the effectiveness of BiPer in benchmark datasets and network architectures, with improvements of up to 1% and 0.69% with respect to state-of-the-art methods in the classification task over CIFAR-10 and ImageNet, respectively. Our code is publicly available at https://github.com/edmav4/BiPer.
Factor Graph Processing for Dual-Blind Deconvolution at ISAC Receiver
Oct 22, 2023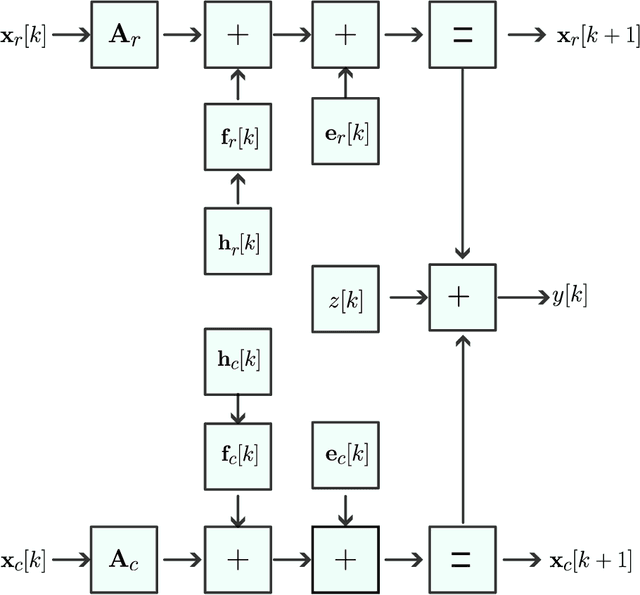

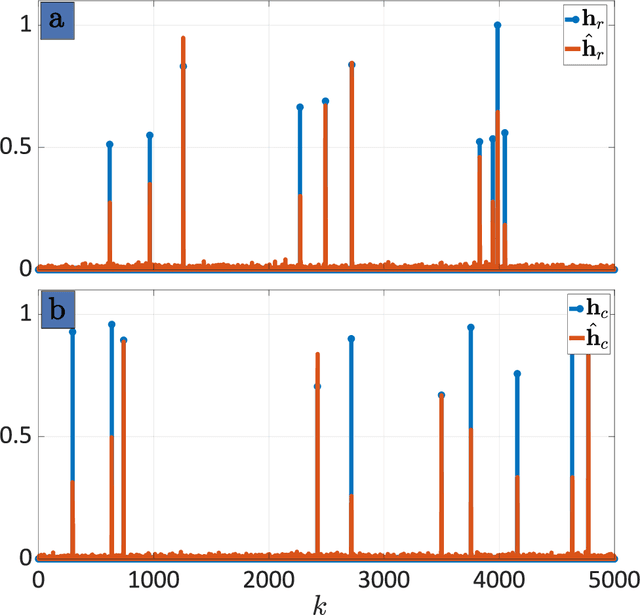
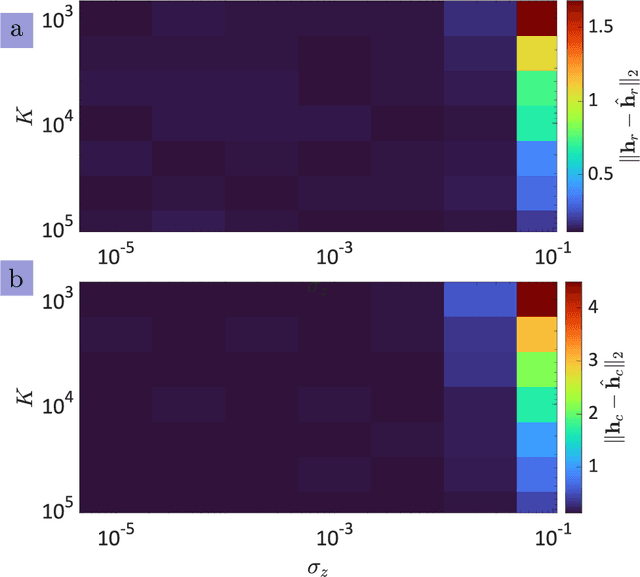
Abstract:Integrated sensing and communications (ISAC) systems have gained significant interest because of their ability to jointly and efficiently access, utilize, and manage the scarce electromagnetic spectrum. The co-existence approach toward ISAC focuses on the receiver processing of overlaid radar and communications signals coming from independent transmitters. A specific ISAC coexistence problem is dual-blind deconvolution (DBD), wherein the transmit signals and channels of both radar and communications are unknown to the receiver. Prior DBD works ignore the evolution of the signal model over time. In this work, we consider a dynamic DBD scenario using a linear state space model (LSSM) such that, apart from the transmit signals and channels of both systems, the LSSM parameters are also unknown. We employ a factor graph representation to model these unknown variables. We avoid the conventional matrix inversion approach to estimate the unknown variables by using an efficient expectation-maximization algorithm, where each iteration employs a Gaussian message passing over the factor graph structure. Numerical experiments demonstrate the accurate estimation of radar and communications channels, including in the presence of noise.
Depth Estimation from a Single Optical Encoded Image using a Learned Colored-Coded Aperture
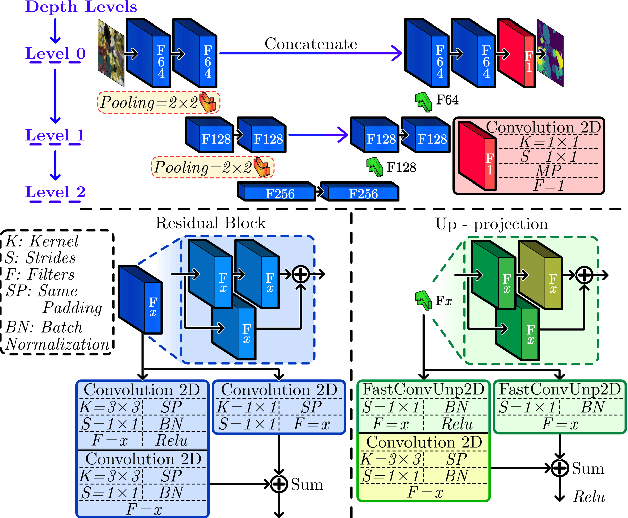
Sep 14, 2023Abstract:Depth estimation from a single image of a conventional camera is a challenging task since depth cues are lost during the acquisition process. State-of-the-art approaches improve the discrimination between different depths by introducing a binary-coded aperture (CA) in the lens aperture that generates different coded blur patterns at different depths. Color-coded apertures (CCA) can also produce color misalignment in the captured image which can be utilized to estimate disparity. Leveraging advances in deep learning, more recent works have explored the data-driven design of a diffractive optical element (DOE) for encoding depth information through chromatic aberrations. However, compared with binary CA or CCA, DOEs are more expensive to fabricate and require high-precision devices. Different from previous CCA-based approaches that employ few basic colors, in this work we propose a CCA with a greater number of color filters and richer spectral information to optically encode relevant depth information in a single snapshot. Furthermore, we propose to jointly learn the color-coded aperture (CCA) pattern and a convolutional neural network (CNN) to retrieve depth information by using an end-to-end optimization approach. We demonstrate through different experiments on three different data sets that the designed color-encoding has the potential to remove depth ambiguities and provides better depth estimates compared to state-of-the-art approaches. Additionally, we build a low-cost prototype of our CCA using a photographic film and validate the proposed approach in real scenarios.
Multi-Antenna Dual-Blind Deconvolution for Joint Radar-Communications via SoMAN Minimization
Mar 23, 2023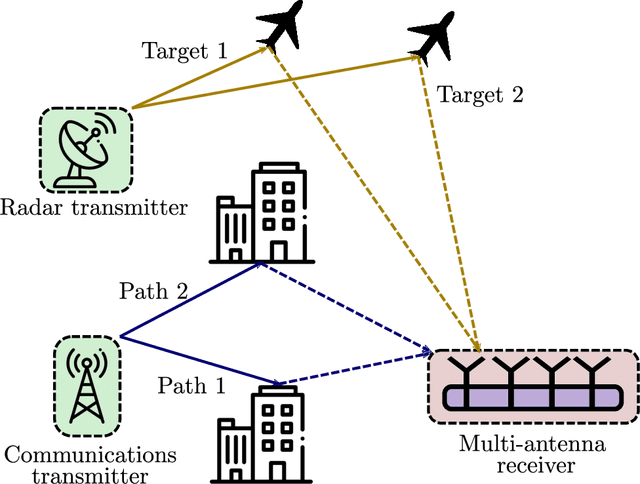
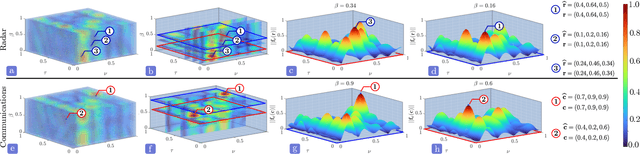
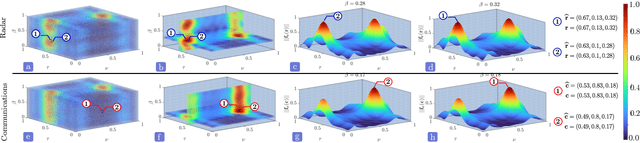
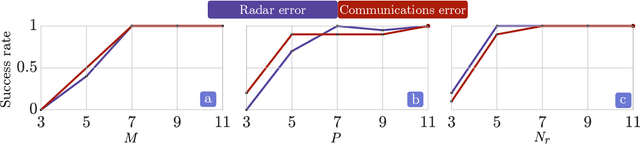
Abstract:Joint radar-communications (JRC) has emerged as a promising technology for efficiently using the limited electromagnetic spectrum. In JRC applications such as secure military receivers, often the radar and communications signals are overlaid in the received signal. In these passive listening outposts, the signals and channels of both radar and communications are unknown to the receiver. The ill-posed problem of recovering all signal and channel parameters from the overlaid signal is terms as dual-blind deconvolution (DBD). In this work, we investigate a more challenging version of DBD with a multi-antenna receiver. We model the radar and communications channels with a few (sparse) continuous-valued parameters such as time delays, Doppler velocities, and directions-of-arrival (DoAs). To solve this highly ill-posed DBD, we propose to minimize the sum of multivariate atomic norms (SoMAN) that depends on the unknown parameters. To this end, we devise an exact semidefinite program using theories of positive hyperoctant trigonometric polynomials (PhTP). Our theoretical analyses show that the minimum number of samples and antennas required for perfect recovery is logarithmically dependent on the maximum of the number of radar targets and communications paths rather than their sum. We show that our approach is easily generalized to include several practical issues such as gain/phase errors and additive noise. Numerical experiments show the exact parameter recovery for different JRC
Coordinate-Based Seismic Interpolation in Irregular Land Survey: A Deep Internal Learning Approach
Nov 21, 2022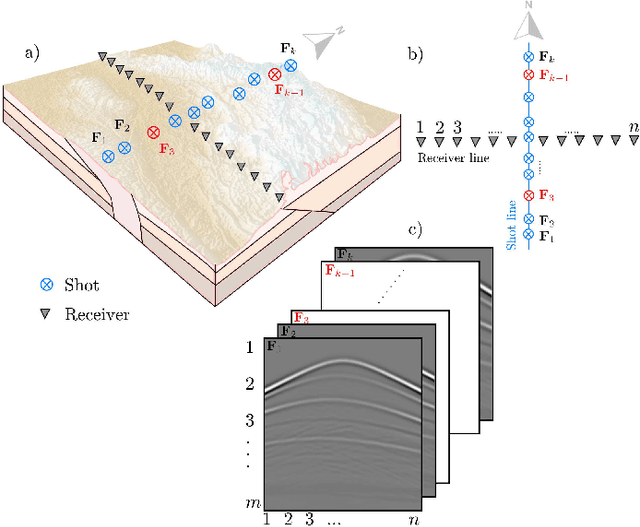
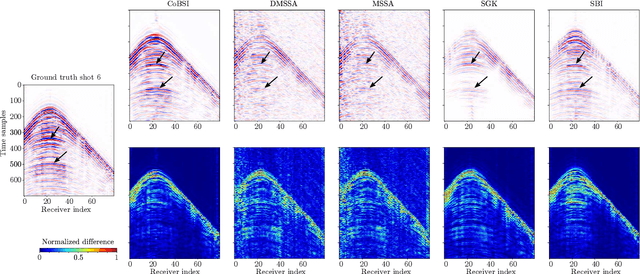
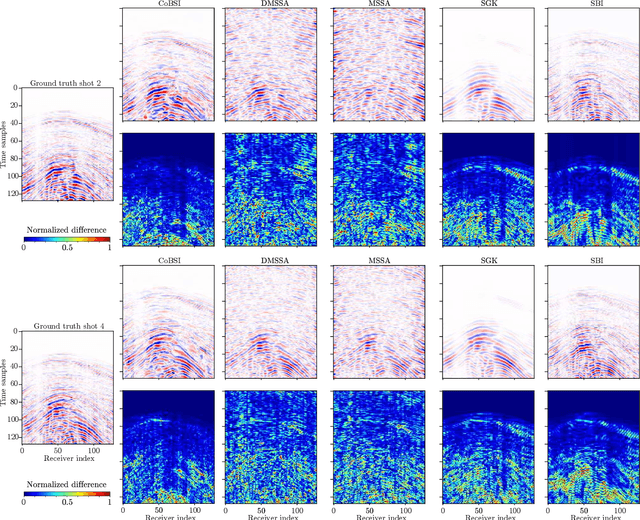
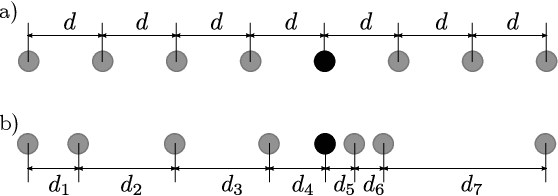
Abstract:Physical and budget constraints often result in irregular sampling, which complicates accurate subsurface imaging. Pre-processing approaches, such as missing trace or shot interpolation, are typically employed to enhance seismic data in such cases. Recently, deep learning has been used to address the trace interpolation problem at the expense of large amounts of training data to adequately represent typical seismic events. Nonetheless, state-of-the-art works have mainly focused on trace reconstruction, with little attention having been devoted to shot interpolation. Furthermore, existing methods assume regularly spaced receivers/sources failing in approximating seismic data from real (irregular) surveys. This work presents a novel shot gather interpolation approach which uses a continuous coordinate-based representation of the acquired seismic wavefield parameterized by a neural network. The proposed unsupervised approach, which we call coordinate-based seismic interpolation (CoBSI), enables the prediction of specific seismic characteristics in irregular land surveys without using external data during neural network training. Experimental results on real and synthetic 3D data validate the ability of the proposed method to estimate continuous smooth seismic events in the time-space and frequency-wavenumber domains, improving sparsity or low rank-based interpolation methods.
Beurling-Selberg Extremization for Dual-Blind Deconvolution Recovery in Joint Radar-Communications
Nov 18, 2022


Abstract:Recent interest in integrated sensing and communications has led to the design of novel signal processing techniques to recover information from an overlaid radar-communications signal. Here, we focus on a spectral coexistence scenario, wherein the channels and transmit signals of both radar and communications systems are unknown to the common receiver. In this dual-blind deconvolution (DBD) problem, the receiver admits a multi-carrier wireless communications signal that is overlaid with the radar signal reflected off multiple targets. The communications and radar channels are represented by continuous-valued range-times or delays corresponding to multiple transmission paths and targets, respectively. Prior works addressed recovery of unknown channels and signals in this ill-posed DBD problem through atomic norm minimization but contingent on individual minimum separation conditions for radar and communications channels. In this paper, we provide an optimal joint separation condition using extremal functions from the Beurling-Selberg interpolation theory. Thereafter, we formulate DBD as a low-rank modified Hankel matrix retrieval and solve it via nuclear norm minimization. We estimate the unknown target and communications parameters from the recovered low-rank matrix using multiple signal classification (MUSIC) method. We show that the joint separation condition also guarantees that the underlying Vandermonde matrix for MUSIC is well-conditioned. Numerical experiments validate our theoretical findings.
Fast Disparity Estimation from a Single Compressed Light Field Measurement
Sep 22, 2022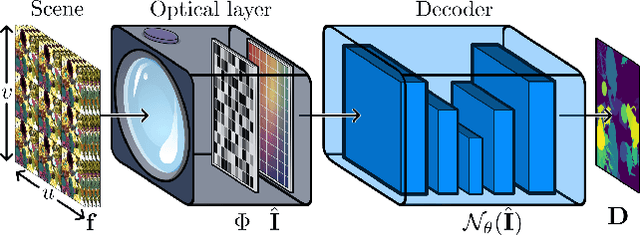


Abstract:The abundant spatial and angular information from light fields has allowed the development of multiple disparity estimation approaches. However, the acquisition of light fields requires high storage and processing cost, limiting the use of this technology in practical applications. To overcome these drawbacks, the compressive sensing (CS) theory has allowed the development of optical architectures to acquire a single coded light field measurement. This measurement is decoded using an optimization algorithm or deep neural network that requires high computational costs. The traditional approach for disparity estimation from compressed light fields requires first recovering the entire light field and then a post-processing step, thus requiring long times. In contrast, this work proposes a fast disparity estimation from a single compressed measurement by omitting the recovery step required in traditional approaches. Specifically, we propose to jointly optimize an optical architecture for acquiring a single coded light field snapshot and a convolutional neural network (CNN) for estimating the disparity maps. Experimentally, the proposed method estimates disparity maps comparable with those obtained from light fields reconstructed using deep learning approaches. Furthermore, the proposed method is 20 times faster in training and inference than the best method that estimates the disparity from reconstructed light fields.
Deep Optical Coding Design in Computational Imaging
Jun 27, 2022
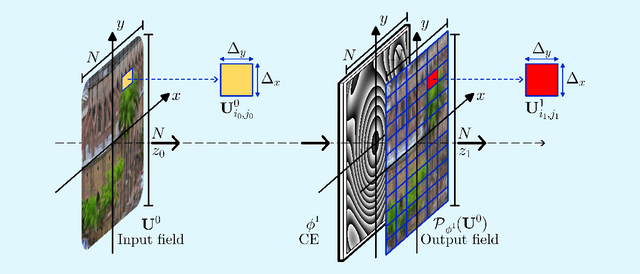
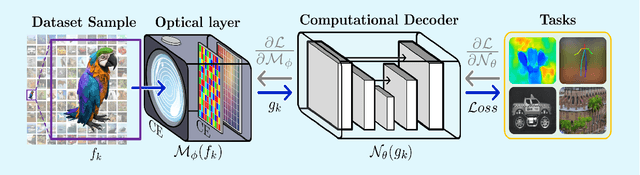
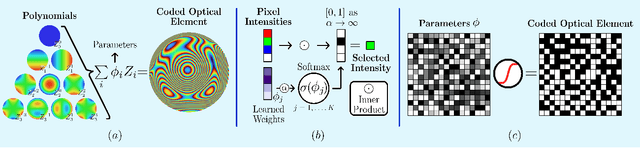
Abstract:Computational optical imaging (COI) systems leverage optical coding elements (CE) in their setups to encode a high-dimensional scene in a single or multiple snapshots and decode it by using computational algorithms. The performance of COI systems highly depends on the design of its main components: the CE pattern and the computational method used to perform a given task. Conventional approaches rely on random patterns or analytical designs to set the distribution of the CE. However, the available data and algorithm capabilities of deep neural networks (DNNs) have opened a new horizon in CE data-driven designs that jointly consider the optical encoder and computational decoder. Specifically, by modeling the COI measurements through a fully differentiable image formation model that considers the physics-based propagation of light and its interaction with the CEs, the parameters that define the CE and the computational decoder can be optimized in an end-to-end (E2E) manner. Moreover, by optimizing just CEs in the same framework, inference tasks can be performed from pure optics. This work surveys the recent advances on CE data-driven design and provides guidelines on how to parametrize different optical elements to include them in the E2E framework. Since the E2E framework can handle different inference applications by changing the loss function and the DNN, we present low-level tasks such as spectral imaging reconstruction or high-level tasks such as pose estimation with privacy preserving enhanced by using optimal task-based optical architectures. Finally, we illustrate classification and 3D object recognition applications performed at the speed of the light using all-optics DNN.
Multi-dimensional dual-blind deconvolution approach toward joint radar-communications
Jun 10, 2022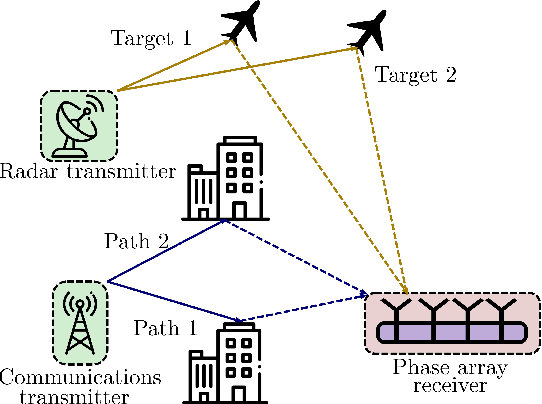

Abstract:We consider a joint multiple-antenna radar-communications system in a co-existence scenario. Contrary to conventional applications, wherein at least the radar waveform and communications channel are known or estimated \textit{a priori}, we investigate the case when the channels and transmit signals of both systems are unknown. In radar applications, this problem arises in multistatic or passive systems, where transmit signal is not known. Similarly, highly dynamic vehicular or mobile communications may render prior estimates of wireless channel unhelpful. In particular, the radar signal reflected-off multiple targets is overlaid with the multi-carrier communications signal. In order to extract the unknown continuous-valued target parameters (range, Doppler velocity, and direction-of-arrival) and communications messages, we formulate the problem as a sparse dual-blind deconvolution and solve it using atomic norm minimization. Numerical experiments validate our proposed approach and show that precise estimation of continuous-valued channel parameters, radar waveform, and communications messages is possible up to scaling ambiguities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge