CLuP-Based Dual-Deconvolution in Automotive ISAC Scenarios

Accurate target parameter estimation of range, velocity, and angle is essential for vehicle safety in advanced driver assistance systems (ADAS) and autonomous vehicles. To enable spectrum sharing, ADAS may employ integrated sensing and communications (ISAC). This paper examines a dual-deconvolution automotive ISAC scenario where the radar waveform is known but the propagation channel is not, while in the communications domain, the channel is known but the transmitted message is not. Conventional maximum likelihood (ML) estimation for automotive target parameters is computationally demanding. To address this, we propose a low-complexity approach using the controlled loosening-up (CLuP) algorithm, which employs iterative refinement for efficient separation and estimation of radar targets. We achieve this through a nuclear norm restriction that stabilizes the problem. Numerical experiments demonstrate the robustness of this approach under high-mobility and noisy automotive environments, highlighting CLuP's potential as a scalable, real-time solution for ISAC in future vehicular networks.

Beurling-Selberg Extremization for Dual-Blind Deconvolution Recovery in Joint Radar-Communications

Recent interest in integrated sensing and communications has led to the design of novel signal processing techniques to recover information from an overlaid radar-communications signal. Here, we focus on a spectral coexistence scenario, wherein the channels and transmit signals of both radar and communications systems are unknown to the common receiver. In this dual-blind deconvolution (DBD) problem, the receiver admits a multi-carrier wireless communications signal that is overlaid with the radar signal reflected off multiple targets. The communications and radar channels are represented by continuous-valued range-times or delays corresponding to multiple transmission paths and targets, respectively. Prior works addressed recovery of unknown channels and signals in this ill-posed DBD problem through atomic norm minimization but contingent on individual minimum separation conditions for radar and communications channels. In this paper, we provide an optimal joint separation condition using extremal functions from the Beurling-Selberg interpolation theory. Thereafter, we formulate DBD as a low-rank modified Hankel matrix retrieval and solve it via nuclear norm minimization. We estimate the unknown target and communications parameters from the recovered low-rank matrix using multiple signal classification (MUSIC) method. We show that the joint separation condition also guarantees that the underlying Vandermonde matrix for MUSIC is well-conditioned. Numerical experiments validate our theoretical findings.

Covariance Estimation from Compressive Data Partitions using a Projected Gradient-based Algorithm

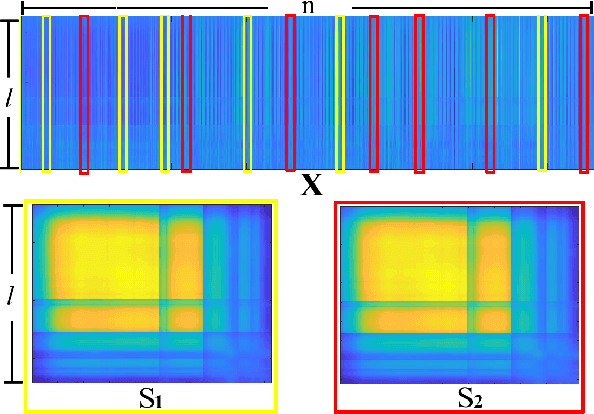
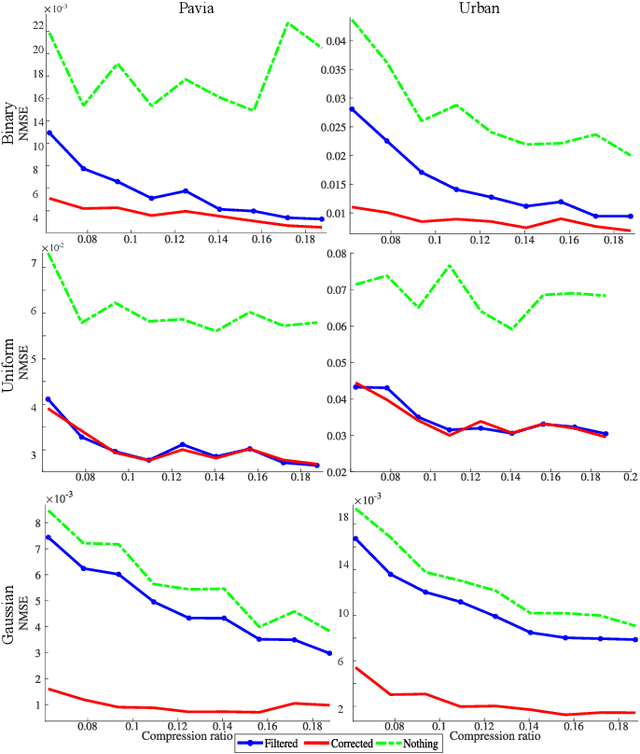
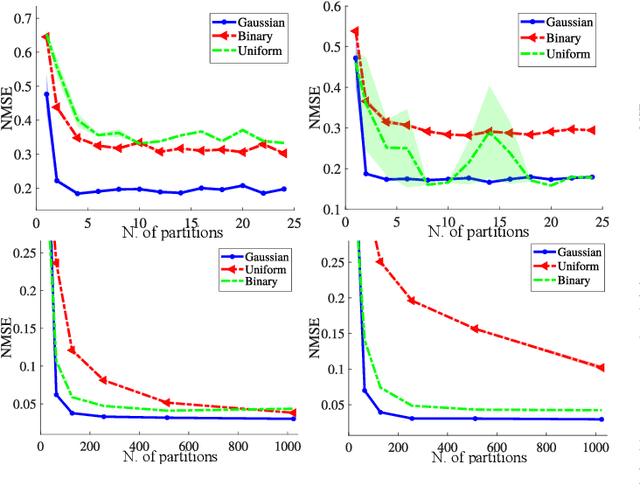
Covariance matrix estimation techniques require high acquisition costs that challenge the sampling systems' storing and transmission capabilities. For this reason, various acquisition approaches have been developed to simultaneously sense and compress the relevant information of the signal using random projections. However, estimating the covariance matrix from the random projections is an ill-posed problem that requires further information about the data, such as sparsity, low rank, or stationary behavior. Furthermore, this approach fails using high compression ratios. Therefore, this paper proposes an algorithm based on the projected gradient method to recover a low-rank or Toeplitz approximation of the covariance matrix. The proposed algorithm divides the data into subsets projected onto different subspaces, assuming that each subset contains an approximation of the signal statistics, improving the inverse problem's condition. The error induced by this assumption is analytically derived along with the convergence guarantees of the proposed method. Extensive simulations show that the proposed algorithm can effectively recover the covariance matrix of hyperspectral images with high compression ratios (8-15% approx) in noisy scenarios. Additionally, simulations and theoretical results show that filtering the gradient reduces the estimator's error recovering up to twice the number of eigenvectors.