Stealth Attacks Against Moving Target Defense for Smart Grid

Data injection attacks (DIAs) pose a significant cybersecurity threat to the Smart Grid by enabling an attacker to compromise the integrity of data acquisition and manipulate estimated states without triggering bad data detection procedures. To mitigate this vulnerability, the moving target defense (MTD) alters branch admittances to mismatch the system information that is available to an attacker, thereby inducing an imperfect DIA construction that results in degradation of attack performance. In this paper, we first analyze the existence of stealth attacks for the case in which the MTD strategy only changes the admittance of a single branch. Equipped with this initial insight, we then extend the results to the case in which multiple branches are protected by the MTD strategy. Remarkably, we show that stealth attacks can be constructed with information only about which branches are protected, without knowledge about the particular admittance value changes. Furthermore, we provide a sufficient protection condition for the MTD strategy via graph-theoretic tools that guarantee that the system is not vulnerable to DIAs. Numerical simulations are implemented on IEEE test systems to validate the obtained results.

Equivalence of the Empirical Risk Minimization to Regularization on the Family of f-Divergences

The solution to empirical risk minimization with $f$-divergence regularization (ERM-$f$DR) is presented under mild conditions on $f$. Under such conditions, the optimal measure is shown to be unique. Examples of the solution for particular choices of the function $f$ are presented. Previously known solutions to common regularization choices are obtained by leveraging the flexibility of the family of $f$-divergences. These include the unique solutions to empirical risk minimization with relative entropy regularization (Type-I and Type-II). The analysis of the solution unveils the following properties of $f$-divergences when used in the ERM-$f$DR problem: $i\bigl)$ $f$-divergence regularization forces the support of the solution to coincide with the support of the reference measure, which introduces a strong inductive bias that dominates the evidence provided by the training data; and $ii\bigl)$ any $f$-divergence regularization is equivalent to a different $f$-divergence regularization with an appropriate transformation of the empirical risk function.

Generalization Analysis of Machine Learning Algorithms via the Worst-Case Data-Generating Probability Measure

In this paper, the worst-case probability measure over the data is introduced as a tool for characterizing the generalization capabilities of machine learning algorithms. More specifically, the worst-case probability measure is a Gibbs probability measure and the unique solution to the maximization of the expected loss under a relative entropy constraint with respect to a reference probability measure. Fundamental generalization metrics, such as the sensitivity of the expected loss, the sensitivity of the empirical risk, and the generalization gap are shown to have closed-form expressions involving the worst-case data-generating probability measure. Existing results for the Gibbs algorithm, such as characterizing the generalization gap as a sum of mutual information and lautum information, up to a constant factor, are recovered. A novel parallel is established between the worst-case data-generating probability measure and the Gibbs algorithm. Specifically, the Gibbs probability measure is identified as a fundamental commonality of the model space and the data space for machine learning algorithms.

On the Validation of Gibbs Algorithms: Training Datasets, Test Datasets and their Aggregation

The dependence on training data of the Gibbs algorithm (GA) is analytically characterized. By adopting the expected empirical risk as the performance metric, the sensitivity of the GA is obtained in closed form. In this case, sensitivity is the performance difference with respect to an arbitrary alternative algorithm. This description enables the development of explicit expressions involving the training errors and test errors of GAs trained with different datasets. Using these tools, dataset aggregation is studied and different figures of merit to evaluate the generalization capabilities of GAs are introduced. For particular sizes of such datasets and parameters of the GAs, a connection between Jeffrey's divergence, training and test errors is established.

Analysis of the Relative Entropy Asymmetry in the Regularization of Empirical Risk Minimization

The effect of the relative entropy asymmetry is analyzed in the empirical risk minimization with relative entropy regularization (ERM-RER) problem. A novel regularization is introduced, coined Type-II regularization, that allows for solutions to the ERM-RER problem with a support that extends outside the support of the reference measure. The solution to the new ERM-RER Type-II problem is analytically characterized in terms of the Radon-Nikodym derivative of the reference measure with respect to the solution. The analysis of the solution unveils the following properties of relative entropy when it acts as a regularizer in the ERM-RER problem: i) relative entropy forces the support of the Type-II solution to collapse into the support of the reference measure, which introduces a strong inductive bias that dominates the evidence provided by the training data; ii) Type-II regularization is equivalent to classical relative entropy regularization with an appropriate transformation of the empirical risk function. Closed-form expressions of the expected empirical risk as a function of the regularization parameters are provided.

Empirical Risk Minimization with Generalized Relative Entropy Regularization

The empirical risk minimization (ERM) problem with relative entropy regularization (ERM-RER) is investigated under the assumption that the reference measure is a~$\sigma$-finite measure instead of a probability measure. This assumption leads to a generalization of the ERM-RER (g-ERM-RER) problem that allows for a larger degree of flexibility in the incorporation of prior knowledge over the set of models. The solution of the g-ERM-RER problem is shown to be a unique probability measure mutually absolutely continuous with the reference measure and to exhibit a probably-approximately-correct (PAC) guarantee for the ERM problem. For a given dataset, the empirical risk is shown to be a sub-Gaussian random variable when the models are sampled from the solution to the g-ERM-RER problem. Finally, the sensitivity of the expected empirical risk to deviations from the solution of the g-ERM-RER problem is studied. In particular, the expectation of the absolute value of sensitivity is shown to be upper bounded, up to a constant factor, by the square root of the lautum information between the models and the datasets.

Empirical Risk Minimization with Relative Entropy Regularization: Optimality and Sensitivity Analysis

The optimality and sensitivity of the empirical risk minimization problem with relative entropy regularization (ERM-RER) are investigated for the case in which the reference is a sigma-finite measure instead of a probability measure. This generalization allows for a larger degree of flexibility in the incorporation of prior knowledge over the set of models. In this setting, the interplay of the regularization parameter, the reference measure, the risk function, and the empirical risk induced by the solution of the ERM-RER problem is characterized. This characterization yields necessary and sufficient conditions for the existence of a regularization parameter that achieves an arbitrarily small empirical risk with arbitrarily high probability. The sensitivity of the expected empirical risk to deviations from the solution of the ERM-RER problem is studied. The sensitivity is then used to provide upper and lower bounds on the expected empirical risk. Moreover, it is shown that the expectation of the sensitivity is upper bounded, up to a constant factor, by the square root of the lautum information between the models and the datasets.

Asymptotic Learning Requirements for Stealth Attacks

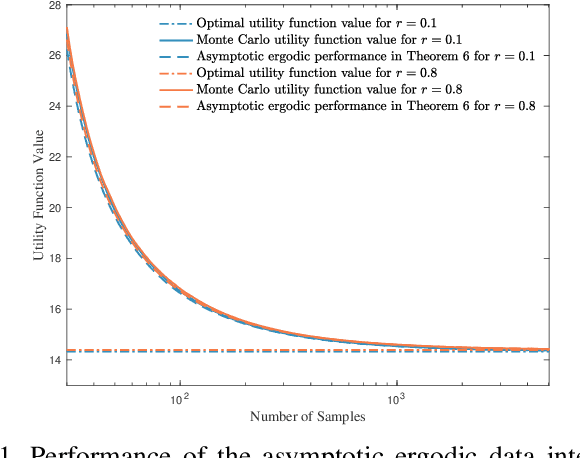
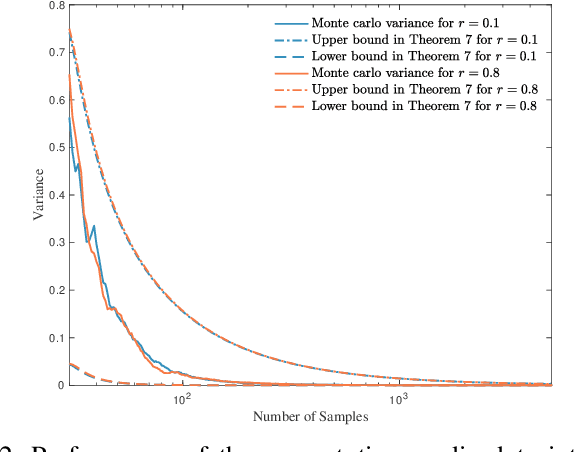
Information-theoretic stealth attacks are data injection attacks that minimize the amount of information acquired by the operator about the state variables, while simultaneously limiting the Kullback-Leibler divergence between the distribution of the measurements under attack and the distribution under normal operation with the aim of controling the probability of detection. For Gaussian distributed state variables, attack construction requires knowledge of the second order statistics of the state variables, which is estimated from a finite number of past realizations using a sample covariance matrix. Within this framework, the attack performance is studied for the attack construction with the sample covariance matrix. This results in an analysis of the amount of data required to learn the covariance matrix of the state variables used on the attack construction. The ergodic attack performance is characterized using asymptotic random matrix theory tools, and the variance of the attack performance is bounded. The ergodic performance and the variance bounds are assessed with simulations on IEEE test systems.

Covariance Estimation from Compressive Data Partitions using a Projected Gradient-based Algorithm

Covariance matrix estimation techniques require high acquisition costs that challenge the sampling systems' storing and transmission capabilities. For this reason, various acquisition approaches have been developed to simultaneously sense and compress the relevant information of the signal using random projections. However, estimating the covariance matrix from the random projections is an ill-posed problem that requires further information about the data, such as sparsity, low rank, or stationary behavior. Furthermore, this approach fails using high compression ratios. Therefore, this paper proposes an algorithm based on the projected gradient method to recover a low-rank or Toeplitz approximation of the covariance matrix. The proposed algorithm divides the data into subsets projected onto different subspaces, assuming that each subset contains an approximation of the signal statistics, improving the inverse problem's condition. The error induced by this assumption is analytically derived along with the convergence guarantees of the proposed method. Extensive simulations show that the proposed algorithm can effectively recover the covariance matrix of hyperspectral images with high compression ratios (8-15% approx) in noisy scenarios. Additionally, simulations and theoretical results show that filtering the gradient reduces the estimator's error recovering up to twice the number of eigenvectors.