Generalization Error of $f$-Divergence Stabilized Algorithms via Duality

The solution to empirical risk minimization with $f$-divergence regularization (ERM-$f$DR) is extended to constrained optimization problems, establishing conditions for equivalence between the solution and constraints. A dual formulation of ERM-$f$DR is introduced, providing a computationally efficient method to derive the normalization function of the ERM-$f$DR solution. This dual approach leverages the Legendre-Fenchel transform and the implicit function theorem, enabling explicit characterizations of the generalization error for general algorithms under mild conditions, and another for ERM-$f$DR solutions.

Asymmetry of the Relative Entropy in the Regularization of Empirical Risk Minimization

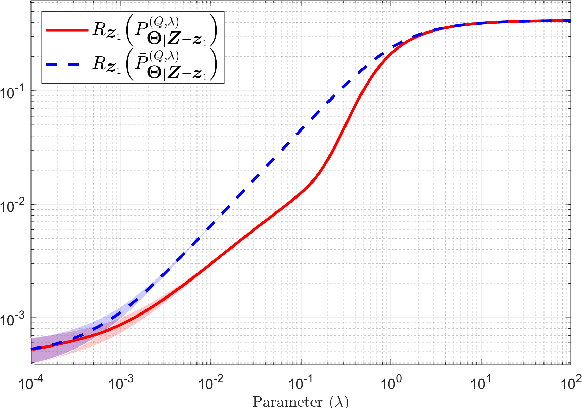
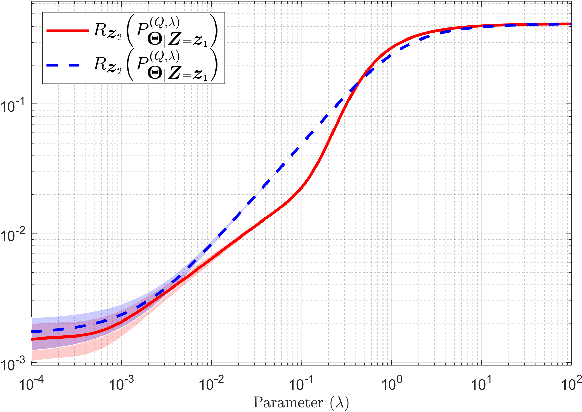
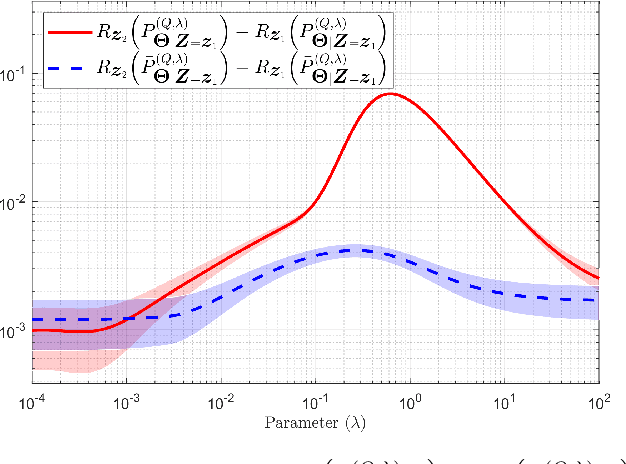
The effect of relative entropy asymmetry is analyzed in the context of empirical risk minimization (ERM) with relative entropy regularization (ERM-RER). Two regularizations are considered: $(a)$ the relative entropy of the measure to be optimized with respect to a reference measure (Type-I ERM-RER); or $(b)$ the relative entropy of the reference measure with respect to the measure to be optimized (Type-II ERM-RER). The main result is the characterization of the solution to the Type-II ERM-RER problem and its key properties. By comparing the well-understood Type-I ERM-RER with Type-II ERM-RER, the effects of entropy asymmetry are highlighted. The analysis shows that in both cases, regularization by relative entropy forces the solution's support to collapse into the support of the reference measure, introducing a strong inductive bias that can overshadow the evidence provided by the training data. Finally, it is shown that Type-II regularization is equivalent to Type-I regularization with an appropriate transformation of the empirical risk function.

Equivalence of the Empirical Risk Minimization to Regularization on the Family of f-Divergences

The solution to empirical risk minimization with $f$-divergence regularization (ERM-$f$DR) is presented under mild conditions on $f$. Under such conditions, the optimal measure is shown to be unique. Examples of the solution for particular choices of the function $f$ are presented. Previously known solutions to common regularization choices are obtained by leveraging the flexibility of the family of $f$-divergences. These include the unique solutions to empirical risk minimization with relative entropy regularization (Type-I and Type-II). The analysis of the solution unveils the following properties of $f$-divergences when used in the ERM-$f$DR problem: $i\bigl)$ $f$-divergence regularization forces the support of the solution to coincide with the support of the reference measure, which introduces a strong inductive bias that dominates the evidence provided by the training data; and $ii\bigl)$ any $f$-divergence regularization is equivalent to a different $f$-divergence regularization with an appropriate transformation of the empirical risk function.

Analysis of the Relative Entropy Asymmetry in the Regularization of Empirical Risk Minimization

The effect of the relative entropy asymmetry is analyzed in the empirical risk minimization with relative entropy regularization (ERM-RER) problem. A novel regularization is introduced, coined Type-II regularization, that allows for solutions to the ERM-RER problem with a support that extends outside the support of the reference measure. The solution to the new ERM-RER Type-II problem is analytically characterized in terms of the Radon-Nikodym derivative of the reference measure with respect to the solution. The analysis of the solution unveils the following properties of relative entropy when it acts as a regularizer in the ERM-RER problem: i) relative entropy forces the support of the Type-II solution to collapse into the support of the reference measure, which introduces a strong inductive bias that dominates the evidence provided by the training data; ii) Type-II regularization is equivalent to classical relative entropy regularization with an appropriate transformation of the empirical risk function. Closed-form expressions of the expected empirical risk as a function of the regularization parameters are provided.