Empirical Risk Minimization with $f$-Divergence Regularization

In this paper, the solution to the empirical risk minimization problem with $f$-divergence regularization (ERM-$f$DR) is presented and conditions under which the solution also serves as the solution to the minimization of the expected empirical risk subject to an $f$-divergence constraint are established. The proposed approach extends applicability to a broader class of $f$-divergences than previously reported and yields theoretical results that recover previously known results. Additionally, the difference between the expected empirical risk of the ERM-$f$DR solution and that of its reference measure is characterized, providing insights into previously studied cases of $f$-divergences. A central contribution is the introduction of the normalization function, a mathematical object that is critical in both the dual formulation and practical computation of the ERM-$f$DR solution. This work presents an implicit characterization of the normalization function as a nonlinear ordinary differential equation (ODE), establishes its key properties, and subsequently leverages them to construct a numerical algorithm for approximating the normalization factor under mild assumptions. Further analysis demonstrates structural equivalences between ERM-$f$DR problems with different $f$-divergences via transformations of the empirical risk. Finally, the proposed algorithm is used to compute the training and test risks of ERM-$f$DR solutions under different $f$-divergence regularizers. This numerical example highlights the practical implications of choosing different functions $f$ in ERM-$f$DR problems.

Generalization Error of $f$-Divergence Stabilized Algorithms via Duality

The solution to empirical risk minimization with $f$-divergence regularization (ERM-$f$DR) is extended to constrained optimization problems, establishing conditions for equivalence between the solution and constraints. A dual formulation of ERM-$f$DR is introduced, providing a computationally efficient method to derive the normalization function of the ERM-$f$DR solution. This dual approach leverages the Legendre-Fenchel transform and the implicit function theorem, enabling explicit characterizations of the generalization error for general algorithms under mild conditions, and another for ERM-$f$DR solutions.

Variations on the Expectation Due to Changes in the Probability Measure

Closed-form expressions are presented for the variation of the expectation of a given function due to changes in the probability measure used for the expectation. They unveil interesting connections with Gibbs probability measures, the mutual information, and the lautum information.

Proofs for Folklore Theorems on the Radon-Nikodym Derivative

Rigorous statements and formal proofs are presented for both foundational and advanced folklore theorems on the Radon-Nikodym derivative. The cases of product and marginal measures are carefully considered; and the hypothesis under which the statements hold are rigorously enumerated.

The Generalization Error of Machine Learning Algorithms

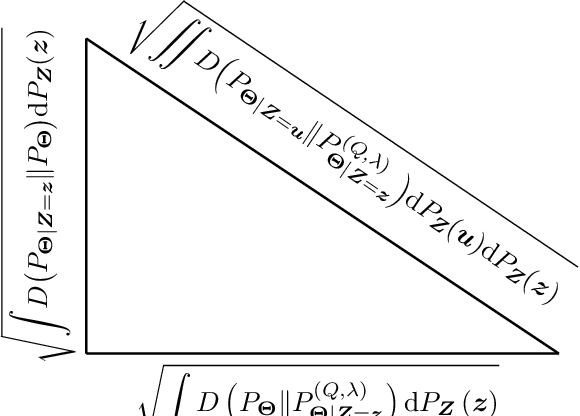
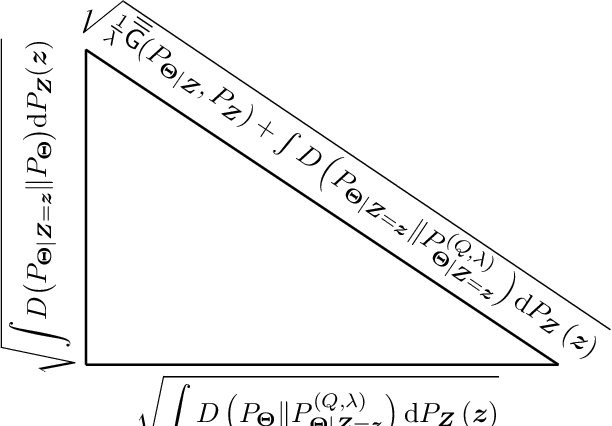
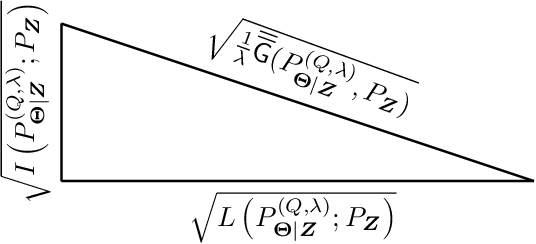
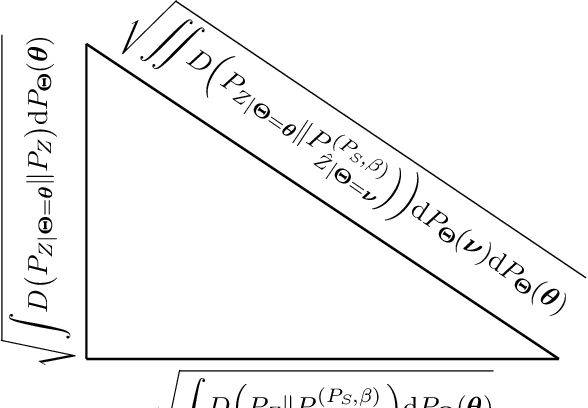
In this paper, the method of gaps, a technique for deriving closed-form expressions in terms of information measures for the generalization error of machine learning algorithms is introduced. The method relies on two central observations: $(a)$~The generalization error is an average of the variation of the expected empirical risk with respect to changes on the probability measure (used for expectation); and~$(b)$~these variations, also referred to as gaps, exhibit closed-form expressions in terms of information measures. The expectation of the empirical risk can be either with respect to a measure on the models (with a fixed dataset) or with respect to a measure on the datasets (with a fixed model), which results in two variants of the method of gaps. The first variant, which focuses on the gaps of the expected empirical risk with respect to a measure on the models, appears to be the most general, as no assumptions are made on the distribution of the datasets. The second variant develops under the assumption that datasets are made of independent and identically distributed data points. All existing exact expressions for the generalization error of machine learning algorithms can be obtained with the proposed method. Also, this method allows obtaining numerous new exact expressions, which improves the understanding of the generalization error; establish connections with other areas in statistics, e.g., hypothesis testing; and potentially, might guide algorithm designs.

Asymmetry of the Relative Entropy in the Regularization of Empirical Risk Minimization

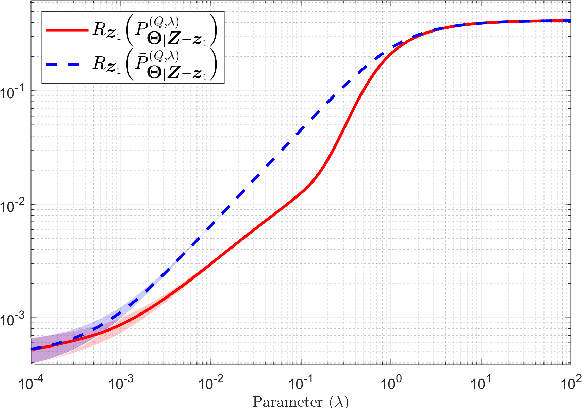
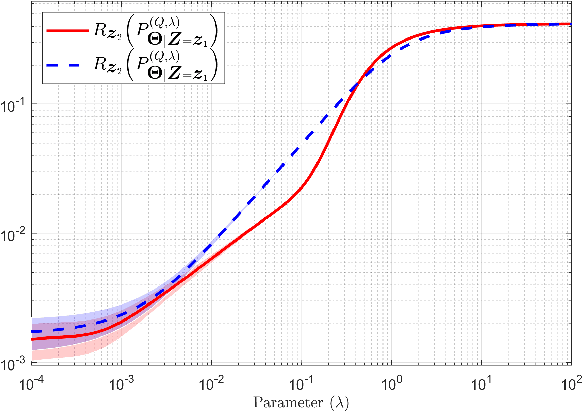
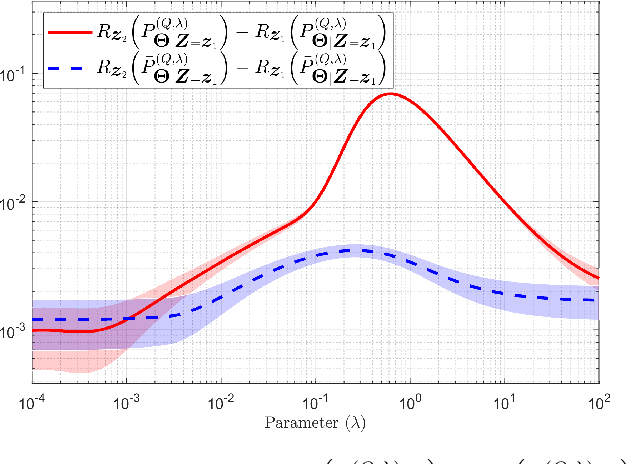
The effect of relative entropy asymmetry is analyzed in the context of empirical risk minimization (ERM) with relative entropy regularization (ERM-RER). Two regularizations are considered: $(a)$ the relative entropy of the measure to be optimized with respect to a reference measure (Type-I ERM-RER); or $(b)$ the relative entropy of the reference measure with respect to the measure to be optimized (Type-II ERM-RER). The main result is the characterization of the solution to the Type-II ERM-RER problem and its key properties. By comparing the well-understood Type-I ERM-RER with Type-II ERM-RER, the effects of entropy asymmetry are highlighted. The analysis shows that in both cases, regularization by relative entropy forces the solution's support to collapse into the support of the reference measure, introducing a strong inductive bias that can overshadow the evidence provided by the training data. Finally, it is shown that Type-II regularization is equivalent to Type-I regularization with an appropriate transformation of the empirical risk function.

Equivalence of the Empirical Risk Minimization to Regularization on the Family of f-Divergences

The solution to empirical risk minimization with $f$-divergence regularization (ERM-$f$DR) is presented under mild conditions on $f$. Under such conditions, the optimal measure is shown to be unique. Examples of the solution for particular choices of the function $f$ are presented. Previously known solutions to common regularization choices are obtained by leveraging the flexibility of the family of $f$-divergences. These include the unique solutions to empirical risk minimization with relative entropy regularization (Type-I and Type-II). The analysis of the solution unveils the following properties of $f$-divergences when used in the ERM-$f$DR problem: $i\bigl)$ $f$-divergence regularization forces the support of the solution to coincide with the support of the reference measure, which introduces a strong inductive bias that dominates the evidence provided by the training data; and $ii\bigl)$ any $f$-divergence regularization is equivalent to a different $f$-divergence regularization with an appropriate transformation of the empirical risk function.

Generalization Analysis of Machine Learning Algorithms via the Worst-Case Data-Generating Probability Measure

In this paper, the worst-case probability measure over the data is introduced as a tool for characterizing the generalization capabilities of machine learning algorithms. More specifically, the worst-case probability measure is a Gibbs probability measure and the unique solution to the maximization of the expected loss under a relative entropy constraint with respect to a reference probability measure. Fundamental generalization metrics, such as the sensitivity of the expected loss, the sensitivity of the empirical risk, and the generalization gap are shown to have closed-form expressions involving the worst-case data-generating probability measure. Existing results for the Gibbs algorithm, such as characterizing the generalization gap as a sum of mutual information and lautum information, up to a constant factor, are recovered. A novel parallel is established between the worst-case data-generating probability measure and the Gibbs algorithm. Specifically, the Gibbs probability measure is identified as a fundamental commonality of the model space and the data space for machine learning algorithms.

On the Validation of Gibbs Algorithms: Training Datasets, Test Datasets and their Aggregation

The dependence on training data of the Gibbs algorithm (GA) is analytically characterized. By adopting the expected empirical risk as the performance metric, the sensitivity of the GA is obtained in closed form. In this case, sensitivity is the performance difference with respect to an arbitrary alternative algorithm. This description enables the development of explicit expressions involving the training errors and test errors of GAs trained with different datasets. Using these tools, dataset aggregation is studied and different figures of merit to evaluate the generalization capabilities of GAs are introduced. For particular sizes of such datasets and parameters of the GAs, a connection between Jeffrey's divergence, training and test errors is established.

Analysis of the Relative Entropy Asymmetry in the Regularization of Empirical Risk Minimization

The effect of the relative entropy asymmetry is analyzed in the empirical risk minimization with relative entropy regularization (ERM-RER) problem. A novel regularization is introduced, coined Type-II regularization, that allows for solutions to the ERM-RER problem with a support that extends outside the support of the reference measure. The solution to the new ERM-RER Type-II problem is analytically characterized in terms of the Radon-Nikodym derivative of the reference measure with respect to the solution. The analysis of the solution unveils the following properties of relative entropy when it acts as a regularizer in the ERM-RER problem: i) relative entropy forces the support of the Type-II solution to collapse into the support of the reference measure, which introduces a strong inductive bias that dominates the evidence provided by the training data; ii) Type-II regularization is equivalent to classical relative entropy regularization with an appropriate transformation of the empirical risk function. Closed-form expressions of the expected empirical risk as a function of the regularization parameters are provided.