Generalization Analysis of Machine Learning Algorithms via the Worst-Case Data-Generating Probability Measure

In this paper, the worst-case probability measure over the data is introduced as a tool for characterizing the generalization capabilities of machine learning algorithms. More specifically, the worst-case probability measure is a Gibbs probability measure and the unique solution to the maximization of the expected loss under a relative entropy constraint with respect to a reference probability measure. Fundamental generalization metrics, such as the sensitivity of the expected loss, the sensitivity of the empirical risk, and the generalization gap are shown to have closed-form expressions involving the worst-case data-generating probability measure. Existing results for the Gibbs algorithm, such as characterizing the generalization gap as a sum of mutual information and lautum information, up to a constant factor, are recovered. A novel parallel is established between the worst-case data-generating probability measure and the Gibbs algorithm. Specifically, the Gibbs probability measure is identified as a fundamental commonality of the model space and the data space for machine learning algorithms.

Graph Neural Network based scheduling : Improved throughput under a generalized interference model

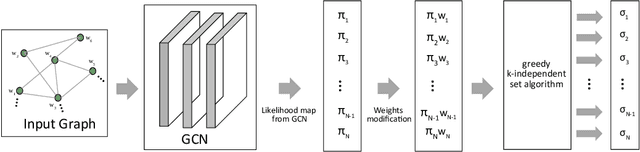
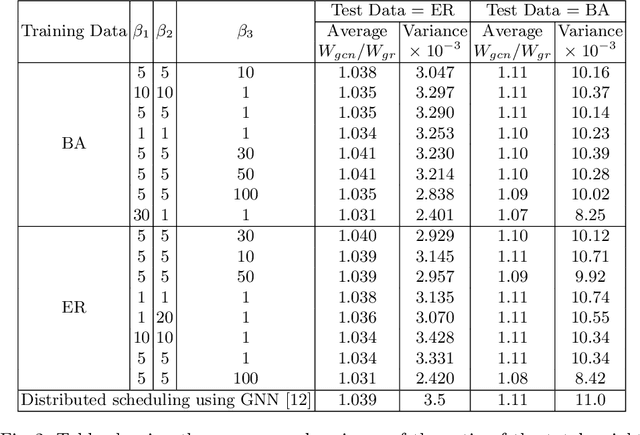
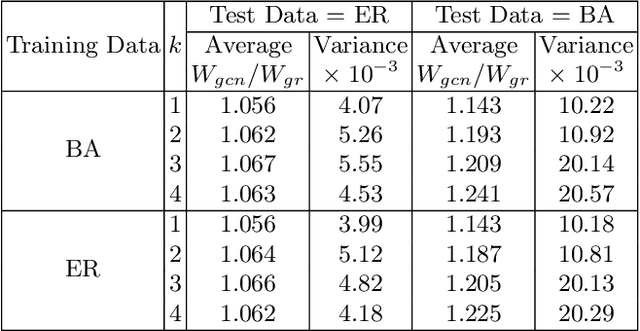
In this work, we propose a Graph Convolutional Neural Networks (GCN) based scheduling algorithm for adhoc networks. In particular, we consider a generalized interference model called the $k$-tolerant conflict graph model and design an efficient approximation for the well-known Max-Weight scheduling algorithm. A notable feature of this work is that the proposed method do not require labelled data set (NP-hard to compute) for training the neural network. Instead, we design a loss function that utilises the existing greedy approaches and trains a GCN that improves the performance of greedy approaches. Our extensive numerical experiments illustrate that using our GCN approach, we can significantly ($4$-$20$ percent) improve the performance of the conventional greedy approach.