The Generalization Error of Machine Learning Algorithms

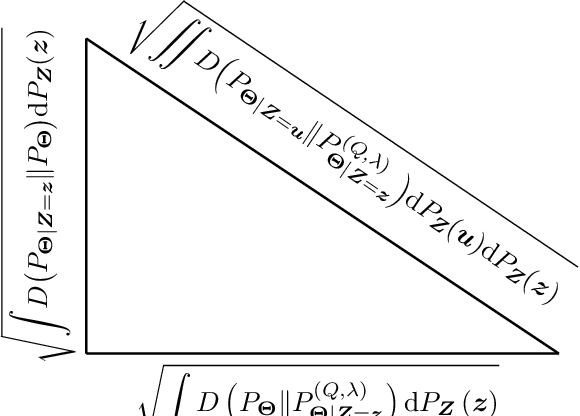
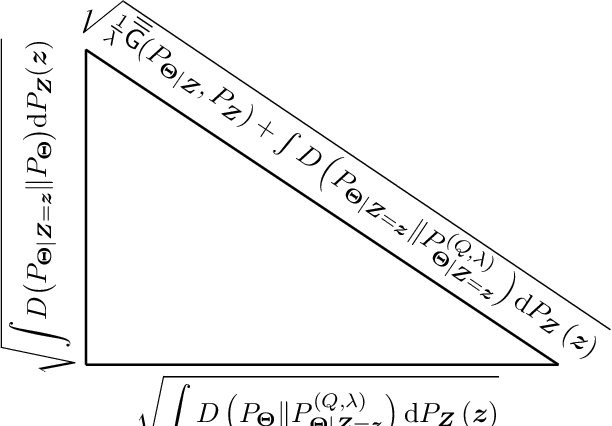
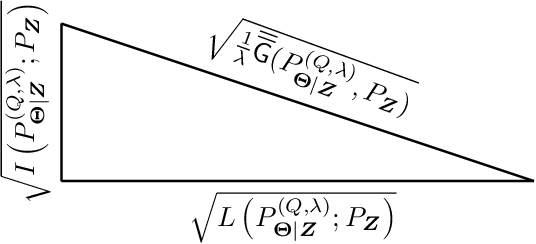
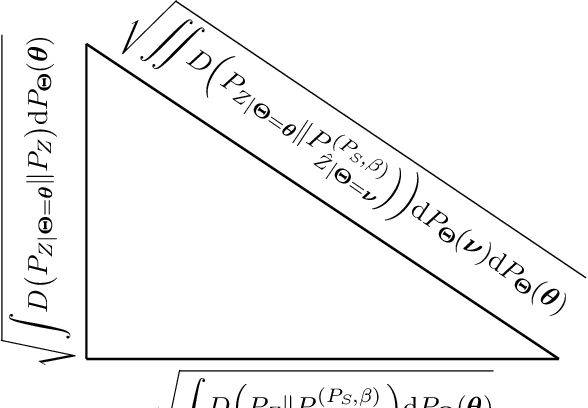
In this paper, the method of gaps, a technique for deriving closed-form expressions in terms of information measures for the generalization error of machine learning algorithms is introduced. The method relies on two central observations: $(a)$~The generalization error is an average of the variation of the expected empirical risk with respect to changes on the probability measure (used for expectation); and~$(b)$~these variations, also referred to as gaps, exhibit closed-form expressions in terms of information measures. The expectation of the empirical risk can be either with respect to a measure on the models (with a fixed dataset) or with respect to a measure on the datasets (with a fixed model), which results in two variants of the method of gaps. The first variant, which focuses on the gaps of the expected empirical risk with respect to a measure on the models, appears to be the most general, as no assumptions are made on the distribution of the datasets. The second variant develops under the assumption that datasets are made of independent and identically distributed data points. All existing exact expressions for the generalization error of machine learning algorithms can be obtained with the proposed method. Also, this method allows obtaining numerous new exact expressions, which improves the understanding of the generalization error; establish connections with other areas in statistics, e.g., hypothesis testing; and potentially, might guide algorithm designs.

Generalization Analysis of Machine Learning Algorithms via the Worst-Case Data-Generating Probability Measure

In this paper, the worst-case probability measure over the data is introduced as a tool for characterizing the generalization capabilities of machine learning algorithms. More specifically, the worst-case probability measure is a Gibbs probability measure and the unique solution to the maximization of the expected loss under a relative entropy constraint with respect to a reference probability measure. Fundamental generalization metrics, such as the sensitivity of the expected loss, the sensitivity of the empirical risk, and the generalization gap are shown to have closed-form expressions involving the worst-case data-generating probability measure. Existing results for the Gibbs algorithm, such as characterizing the generalization gap as a sum of mutual information and lautum information, up to a constant factor, are recovered. A novel parallel is established between the worst-case data-generating probability measure and the Gibbs algorithm. Specifically, the Gibbs probability measure is identified as a fundamental commonality of the model space and the data space for machine learning algorithms.