A Constrained RL Approach for Cost-Efficient Delivery of Latency-Sensitive Applications

Next-generation networks aim to provide performance guarantees to real-time interactive services that require timely and cost-efficient packet delivery. In this context, the goal is to reliably deliver packets with strict deadlines imposed by the application while minimizing overall resource allocation cost. A large body of work has leveraged stochastic optimization techniques to design efficient dynamic routing and scheduling solutions under average delay constraints; however, these methods fall short when faced with strict per-packet delay requirements. We formulate the minimum-cost delay-constrained network control problem as a constrained Markov decision process and utilize constrained deep reinforcement learning (CDRL) techniques to effectively minimize total resource allocation cost while maintaining timely throughput above a target reliability level. Results indicate that the proposed CDRL-based solution can ensure timely packet delivery even when existing baselines fall short, and it achieves lower cost compared to other throughput-maximizing methods.

Estimation of Interference Correlation in mmWave Cellular Systems

We consider a cellular network, where the uplink transmissions to a base station (BS) are interferenced by other devices, a condition that may occur, e.g., in cell-free networks or when using non-orthogonal multiple access (NOMA) techniques. Assuming that the BS treats this interference as additional noise, we focus on the problem of estimating the interference correlation matrix from received signal samples. We consider a BS equipped with multiple antennas and operating in the millimeter-wave (mmWave) bands and propose techniques exploiting the fact that channels comprise only a few reflections at these frequencies. This yields a specific structure of the interference correlation matrix that can be decomposed into three matrices, two rectangular depending on the angle of arrival (AoA) of the interference and the third square with smaller dimensions. We resort to gridless approaches to estimate the AoAs and then project the least square estimate of the interference correlation matrix into a subspace with a smaller dimension, thus reducing the estimation error. Moreover, we derive two simplified estimators, still based on the gridless angle estimation that turns out to be convenient when estimating the interference over a larger number of samples.

Asymptotic Learning Requirements for Stealth Attacks

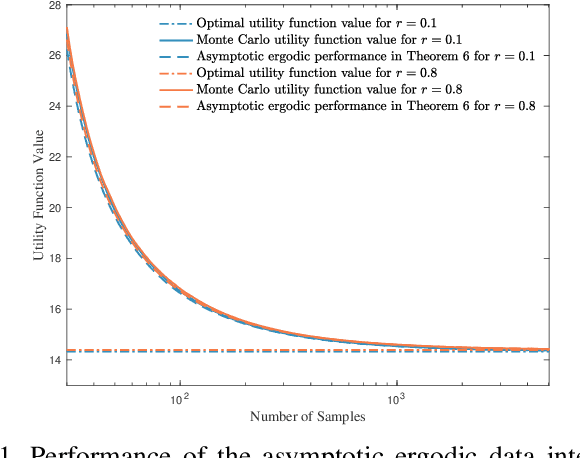
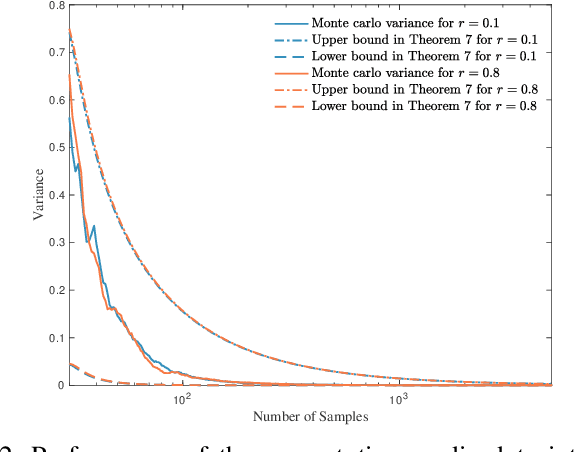
Information-theoretic stealth attacks are data injection attacks that minimize the amount of information acquired by the operator about the state variables, while simultaneously limiting the Kullback-Leibler divergence between the distribution of the measurements under attack and the distribution under normal operation with the aim of controling the probability of detection. For Gaussian distributed state variables, attack construction requires knowledge of the second order statistics of the state variables, which is estimated from a finite number of past realizations using a sample covariance matrix. Within this framework, the attack performance is studied for the attack construction with the sample covariance matrix. This results in an analysis of the amount of data required to learn the covariance matrix of the state variables used on the attack construction. The ergodic attack performance is characterized using asymptotic random matrix theory tools, and the variance of the attack performance is bounded. The ergodic performance and the variance bounds are assessed with simulations on IEEE test systems.