Asymptotic Learning Requirements for Stealth Attacks

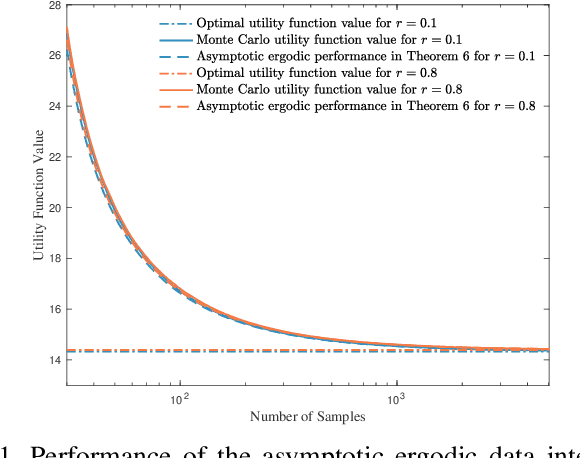
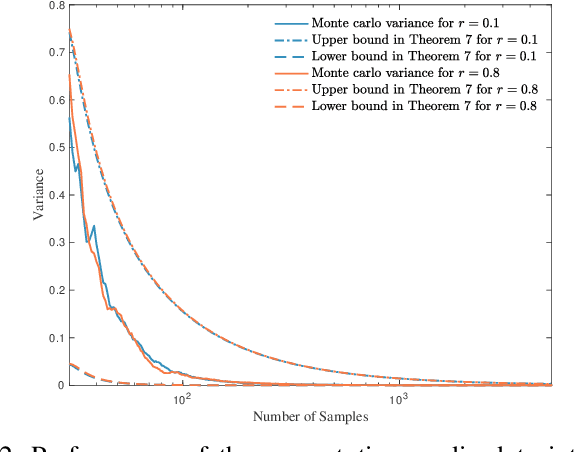
Information-theoretic stealth attacks are data injection attacks that minimize the amount of information acquired by the operator about the state variables, while simultaneously limiting the Kullback-Leibler divergence between the distribution of the measurements under attack and the distribution under normal operation with the aim of controling the probability of detection. For Gaussian distributed state variables, attack construction requires knowledge of the second order statistics of the state variables, which is estimated from a finite number of past realizations using a sample covariance matrix. Within this framework, the attack performance is studied for the attack construction with the sample covariance matrix. This results in an analysis of the amount of data required to learn the covariance matrix of the state variables used on the attack construction. The ergodic attack performance is characterized using asymptotic random matrix theory tools, and the variance of the attack performance is bounded. The ergodic performance and the variance bounds are assessed with simulations on IEEE test systems.