NPN: Non-Linear Projections of the Null-Space for Imaging Inverse Problems

Imaging inverse problems aims to recover high-dimensional signals from undersampled, noisy measurements, a fundamentally ill-posed task with infinite solutions in the null-space of the sensing operator. To resolve this ambiguity, prior information is typically incorporated through handcrafted regularizers or learned models that constrain the solution space. However, these priors typically ignore the task-specific structure of that null-space. In this work, we propose \textit{Non-Linear Projections of the Null-Space} (NPN), a novel class of regularization that, instead of enforcing structural constraints in the image domain, promotes solutions that lie in a low-dimensional projection of the sensing matrix's null-space with a neural network. Our approach has two key advantages: (1) Interpretability: by focusing on the structure of the null-space, we design sensing-matrix-specific priors that capture information orthogonal to the signal components that are fundamentally blind to the sensing process. (2) Flexibility: NPN is adaptable to various inverse problems, compatible with existing reconstruction frameworks, and complementary to conventional image-domain priors. We provide theoretical guarantees on convergence and reconstruction accuracy when used within plug-and-play methods. Empirical results across diverse sensing matrices demonstrate that NPN priors consistently enhance reconstruction fidelity in various imaging inverse problems, such as compressive sensing, deblurring, super-resolution, computed tomography, and magnetic resonance imaging, with plug-and-play methods, unrolling networks, deep image prior, and diffusion models.

DICE: Diffusion Consensus Equilibrium for Sparse-view CT Reconstruction

Sparse-view computed tomography (CT) reconstruction is fundamentally challenging due to undersampling, leading to an ill-posed inverse problem. Traditional iterative methods incorporate handcrafted or learned priors to regularize the solution but struggle to capture the complex structures present in medical images. In contrast, diffusion models (DMs) have recently emerged as powerful generative priors that can accurately model complex image distributions. In this work, we introduce Diffusion Consensus Equilibrium (DICE), a framework that integrates a two-agent consensus equilibrium into the sampling process of a DM. DICE alternates between: (i) a data-consistency agent, implemented through a proximal operator enforcing measurement consistency, and (ii) a prior agent, realized by a DM performing a clean image estimation at each sampling step. By balancing these two complementary agents iteratively, DICE effectively combines strong generative prior capabilities with measurement consistency. Experimental results show that DICE significantly outperforms state-of-the-art baselines in reconstructing high-quality CT images under uniform and non-uniform sparse-view settings of 15, 30, and 60 views (out of a total of 180), demonstrating both its effectiveness and robustness.

UTOPY: Unrolling Algorithm Learning via Fidelity Homotopy for Inverse Problems

Imaging Inverse problems aim to reconstruct an underlying image from undersampled, coded, and noisy observations. Within the wide range of reconstruction frameworks, the unrolling algorithm is one of the most popular due to the synergistic integration of traditional model-based reconstruction methods and modern neural networks, providing an interpretable and highly accurate reconstruction. However, when the sensing operator is highly ill-posed, gradient steps on the data-fidelity term can hinder convergence and degrade reconstruction quality. To address this issue, we propose UTOPY, a homotopy continuation formulation for training the unrolling algorithm. Mainly, this method involves using a well-posed (synthetic) sensing matrix at the beginning of the unrolling network optimization. We define a continuation path strategy to transition smoothly from the synthetic fidelity to the desired ill-posed problem. This strategy enables the network to progressively transition from a simpler, well-posed inverse problem to the more challenging target scenario. We theoretically show that, for projected gradient descent-like unrolling models, the proposed continuation strategy generates a smooth path of unrolling solutions. Experiments on compressive sensing and image deblurring demonstrate that our method consistently surpasses conventional unrolled training, achieving up to 2.5 dB PSNR improvement in reconstruction performance. Source code at

Deep Distillation Gradient Preconditioning for Inverse Problems

Imaging inverse problems are commonly addressed by minimizing measurement consistency and signal prior terms. While huge attention has been paid to developing high-performance priors, even the most advanced signal prior may lose its effectiveness when paired with an ill-conditioned sensing matrix that hinders convergence and degrades reconstruction quality. In optimization theory, preconditioners allow improving the algorithm's convergence by transforming the gradient update. Traditional linear preconditioning techniques enhance convergence, but their performance remains limited due to their dependence on the structure of the sensing matrix. Learning-based linear preconditioners have been proposed, but they are optimized only for data-fidelity optimization, which may lead to solutions in the null-space of the sensing matrix. This paper employs knowledge distillation to design a nonlinear preconditioning operator. In our method, a teacher algorithm using a better-conditioned (synthetic) sensing matrix guides the student algorithm with an ill-conditioned sensing matrix through gradient matching via a preconditioning neural network. We validate our nonlinear preconditioner for plug-and-play FISTA in single-pixel, magnetic resonance, and super-resolution imaging tasks, showing consistent performance improvements and better empirical convergence.

Distilling Knowledge for Designing Computational Imaging Systems

Designing the physical encoder is crucial for accurate image reconstruction in computational imaging (CI) systems. Currently, these systems are designed via end-to-end (E2E) optimization, where the encoder is modeled as a neural network layer and is jointly optimized with the decoder. However, the performance of E2E optimization is significantly reduced by the physical constraints imposed on the encoder. Also, since the E2E learns the parameters of the encoder by backpropagating the reconstruction error, it does not promote optimal intermediate outputs and suffers from gradient vanishing. To address these limitations, we reinterpret the concept of knowledge distillation (KD) for designing a physically constrained CI system by transferring the knowledge of a pretrained, less-constrained CI system. Our approach involves three steps: (1) Given the original CI system (student), a teacher system is created by relaxing the constraints on the student's encoder. (2) The teacher is optimized to solve a less-constrained version of the student's problem. (3) The teacher guides the training of the student through two proposed knowledge transfer functions, targeting both the encoder and the decoder feature space. The proposed method can be employed to any imaging modality since the relaxation scheme and the loss functions can be adapted according to the physical acquisition and the employed decoder. This approach was validated on three representative CI modalities: magnetic resonance, single-pixel, and compressive spectral imaging. Simulations show that a teacher system with an encoder that has a structure similar to that of the student encoder provides effective guidance. Our approach achieves significantly improved reconstruction performance and encoder design, outperforming both E2E optimization and traditional non-data-driven encoder designs.

Learning to reconstruct signals with inexact sensing operator via knowledge distillation

In computational optical imaging and wireless communications, signals are acquired through linear coded and noisy projections, which are recovered through computational algorithms. Deep model-based approaches, i.e., neural networks incorporating the sensing operators, are the state-of-the-art for signal recovery. However, these methods require exact knowledge of the sensing operator, which is often unavailable in practice, leading to performance degradation. Consequently, we propose a new recovery paradigm based on knowledge distillation. A teacher model, trained with full or almost exact knowledge of a synthetic sensing operator, guides a student model with an inexact real sensing operator. The teacher is interpreted as a relaxation of the student since it solves a problem with fewer constraints, which can guide the student to achieve higher performance. We demonstrate the improvement of signal reconstruction in computational optical imaging for single-pixel imaging with miscalibrated coded apertures systems and multiple-input multiple-output symbols detection with inexact channel matrix.

Highly Constrained Coded Aperture Imaging Systems Design Via a Knowledge Distillation Approach

Computational optical imaging (COI) systems have enabled the acquisition of high-dimensional signals through optical coding elements (OCEs). OCEs encode the high-dimensional signal in one or more snapshots, which are subsequently decoded using computational algorithms. Currently, COI systems are optimized through an end-to-end (E2E) approach, where the OCEs are modeled as a layer of a neural network and the remaining layers perform a specific imaging task. However, the performance of COI systems optimized through E2E is limited by the physical constraints imposed by these systems. This paper proposes a knowledge distillation (KD) framework for the design of highly physically constrained COI systems. This approach employs the KD methodology, which consists of a teacher-student relationship, where a high-performance, unconstrained COI system (the teacher), guides the optimization of a physically constrained system (the student) characterized by a limited number of snapshots. We validate the proposed approach, using a binary coded apertures single pixel camera for monochromatic and multispectral image reconstruction. Simulation results demonstrate the superiority of the KD scheme over traditional E2E optimization for the designing of highly physically constrained COI systems.

Learning Point Spread Function Invertibility Assessment for Image Deconvolution

Deep-learning (DL)-based image deconvolution (ID) has exhibited remarkable recovery performance, surpassing traditional linear methods. However, unlike traditional ID approaches that rely on analytical properties of the point spread function (PSF) to achieve high recovery performance - such as specific spectrum properties or small conditional numbers in the convolution matrix - DL techniques lack quantifiable metrics for evaluating PSF suitability for DL-assisted recovery. Aiming to enhance deconvolution quality, we propose a metric that employs a non-linear approach to learn the invertibility of an arbitrary PSF using a neural network by mapping it to a unit impulse. A lower discrepancy between the mapped PSF and a unit impulse indicates a higher likelihood of successful inversion by a DL network. Our findings reveal that this metric correlates with high recovery performance in DL and traditional methods, thereby serving as an effective regularizer in deconvolution tasks. This approach reduces the computational complexity over conventional condition number assessments and is a differentiable process. These useful properties allow its application in designing diffractive optical elements through end-to-end (E2E) optimization, achieving invertible PSFs, and outperforming the E2E baseline framework.

Factor Graph Processing for Dual-Blind Deconvolution at ISAC Receiver

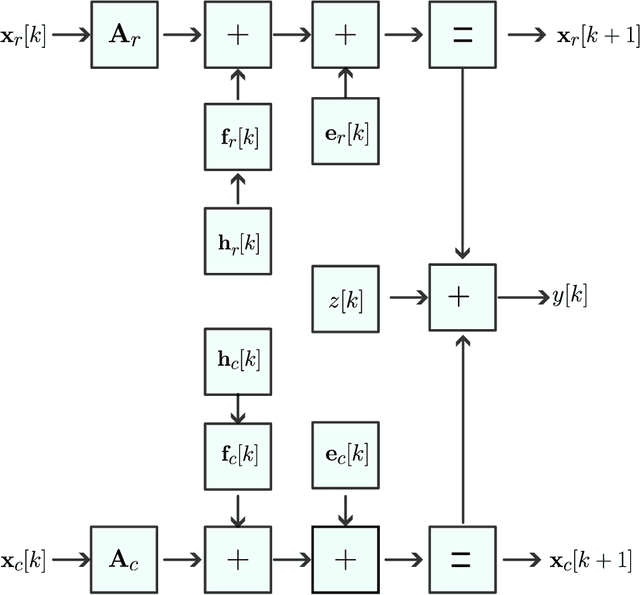
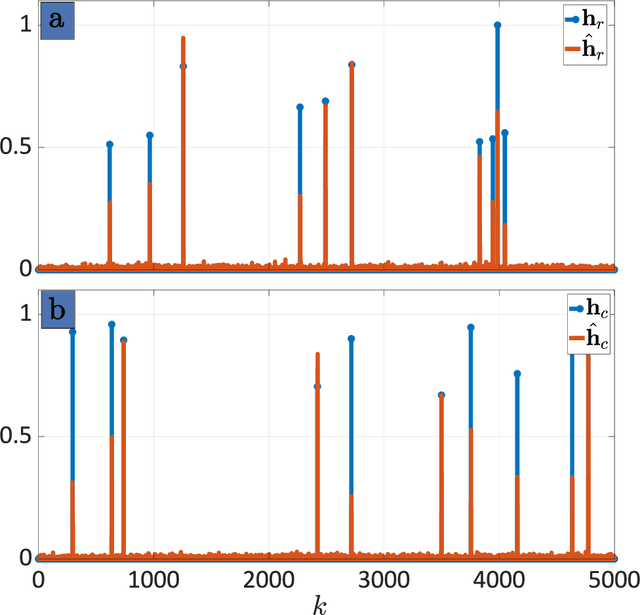
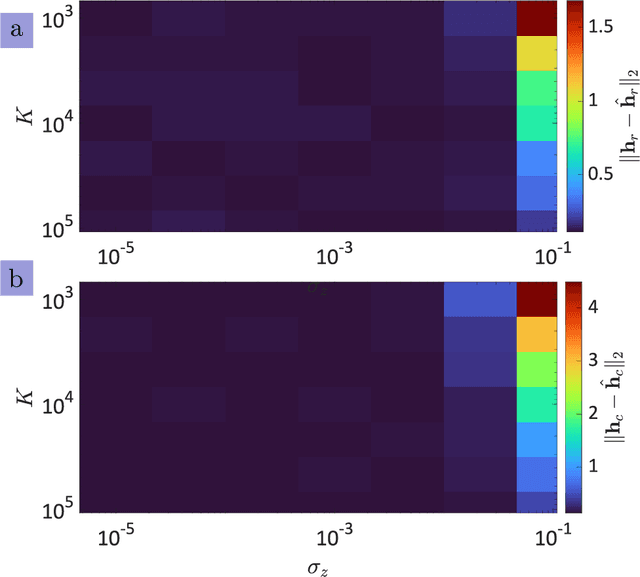
Integrated sensing and communications (ISAC) systems have gained significant interest because of their ability to jointly and efficiently access, utilize, and manage the scarce electromagnetic spectrum. The co-existence approach toward ISAC focuses on the receiver processing of overlaid radar and communications signals coming from independent transmitters. A specific ISAC coexistence problem is dual-blind deconvolution (DBD), wherein the transmit signals and channels of both radar and communications are unknown to the receiver. Prior DBD works ignore the evolution of the signal model over time. In this work, we consider a dynamic DBD scenario using a linear state space model (LSSM) such that, apart from the transmit signals and channels of both systems, the LSSM parameters are also unknown. We employ a factor graph representation to model these unknown variables. We avoid the conventional matrix inversion approach to estimate the unknown variables by using an efficient expectation-maximization algorithm, where each iteration employs a Gaussian message passing over the factor graph structure. Numerical experiments demonstrate the accurate estimation of radar and communications channels, including in the presence of noise.

An Invitation to Hypercomplex Phase Retrieval: Theory and Applications

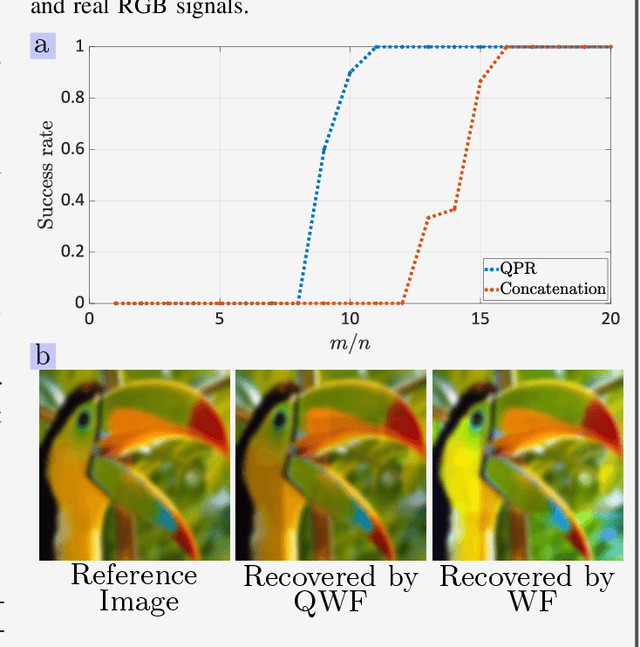
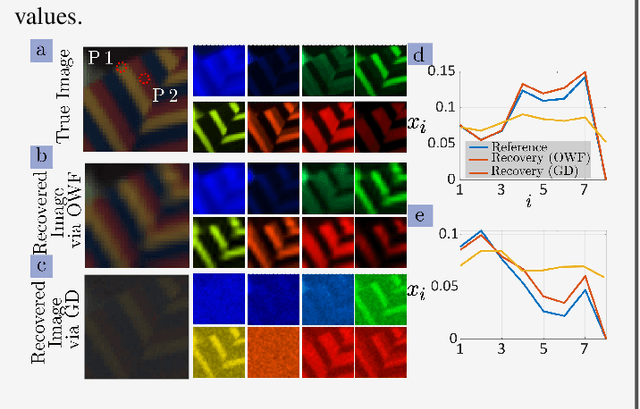
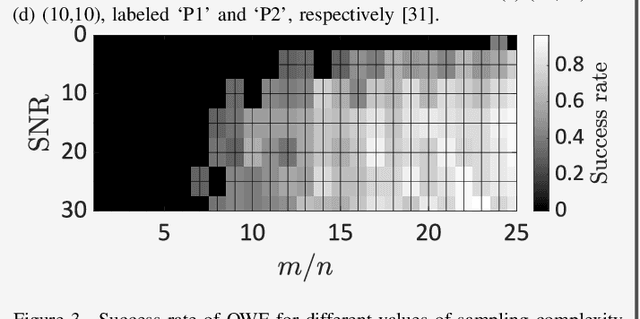
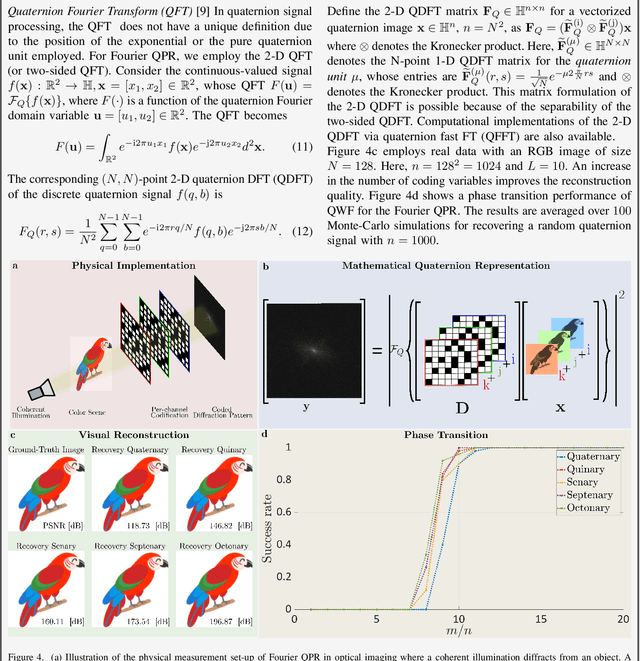
Hypercomplex signal processing (HSP) provides state-of-the-art tools to handle multidimensional signals by harnessing intrinsic correlation of the signal dimensions through Clifford algebra. Recently, the hypercomplex representation of the phase retrieval (PR) problem, wherein a complex-valued signal is estimated through its intensity-only projections, has attracted significant interest. The hypercomplex PR (HPR) arises in many optical imaging and computational sensing applications that usually comprise quaternion and octonion-valued signals. Analogous to the traditional PR, measurements in HPR may involve complex, hypercomplex, Fourier, and other sensing matrices. This set of problems opens opportunities for developing novel HSP tools and algorithms. This article provides a synopsis of the emerging areas and applications of HPR with a focus on optical imaging.