An Invitation to Hypercomplex Phase Retrieval: Theory and Applications
Paper and Code
Oct 20, 2023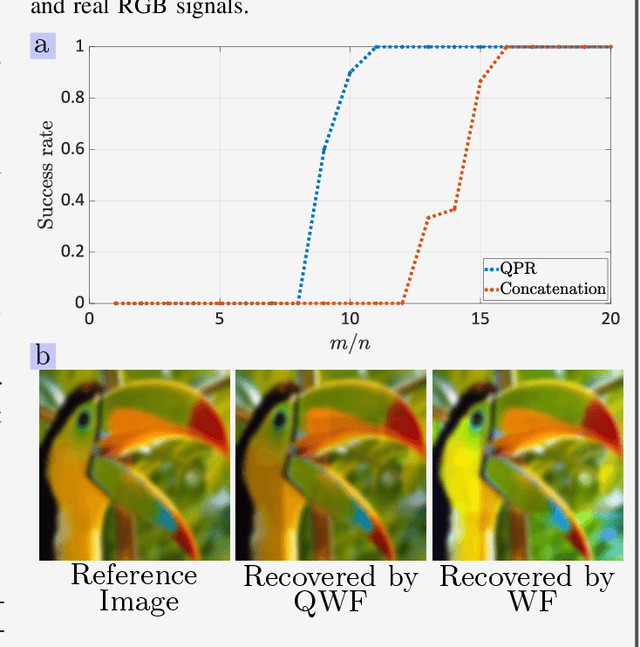
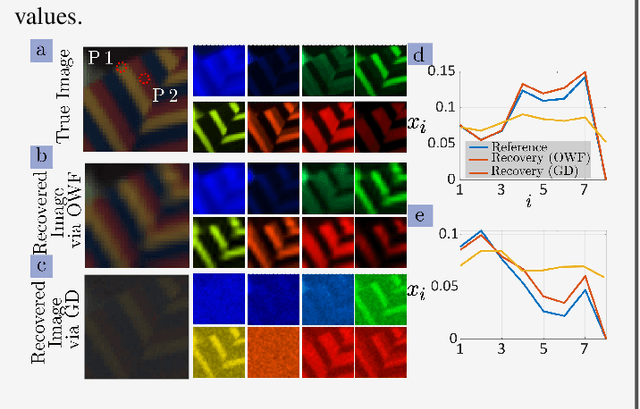
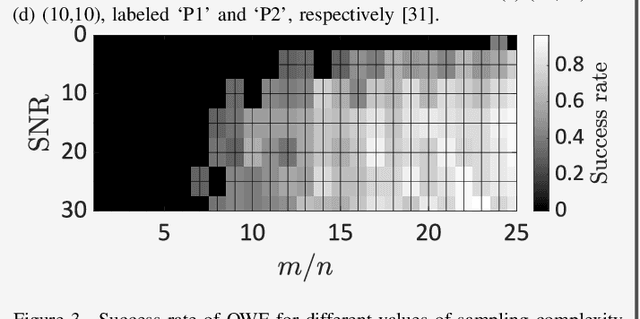
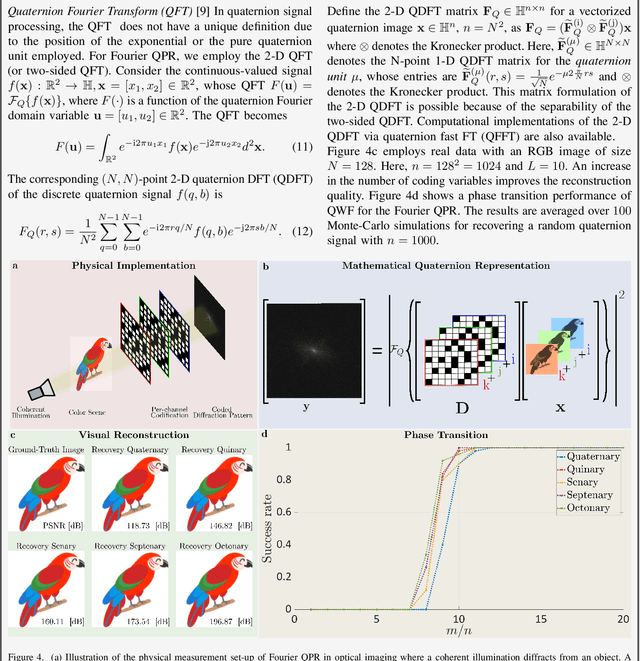
Hypercomplex signal processing (HSP) provides state-of-the-art tools to handle multidimensional signals by harnessing intrinsic correlation of the signal dimensions through Clifford algebra. Recently, the hypercomplex representation of the phase retrieval (PR) problem, wherein a complex-valued signal is estimated through its intensity-only projections, has attracted significant interest. The hypercomplex PR (HPR) arises in many optical imaging and computational sensing applications that usually comprise quaternion and octonion-valued signals. Analogous to the traditional PR, measurements in HPR may involve complex, hypercomplex, Fourier, and other sensing matrices. This set of problems opens opportunities for developing novel HSP tools and algorithms. This article provides a synopsis of the emerging areas and applications of HPR with a focus on optical imaging.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge