Multi-Antenna Dual-Blind Deconvolution for Joint Radar-Communications via SoMAN Minimization

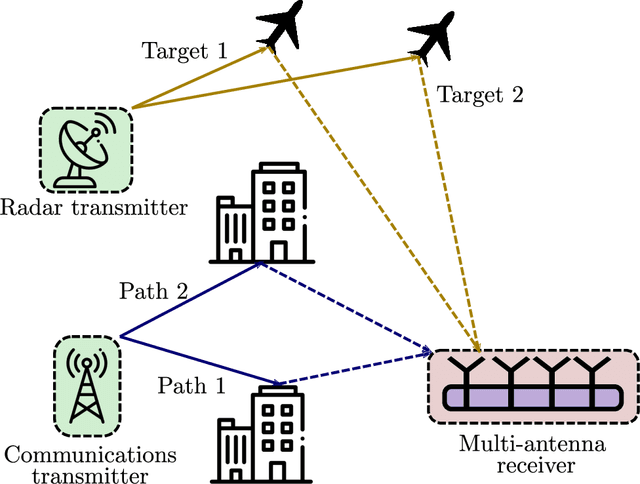
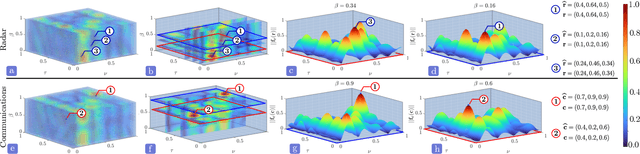
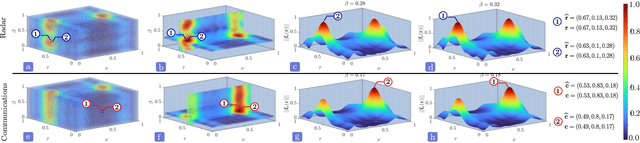
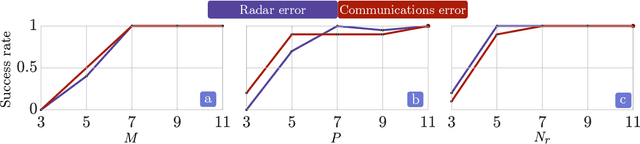
Joint radar-communications (JRC) has emerged as a promising technology for efficiently using the limited electromagnetic spectrum. In JRC applications such as secure military receivers, often the radar and communications signals are overlaid in the received signal. In these passive listening outposts, the signals and channels of both radar and communications are unknown to the receiver. The ill-posed problem of recovering all signal and channel parameters from the overlaid signal is terms as dual-blind deconvolution (DBD). In this work, we investigate a more challenging version of DBD with a multi-antenna receiver. We model the radar and communications channels with a few (sparse) continuous-valued parameters such as time delays, Doppler velocities, and directions-of-arrival (DoAs). To solve this highly ill-posed DBD, we propose to minimize the sum of multivariate atomic norms (SoMAN) that depends on the unknown parameters. To this end, we devise an exact semidefinite program using theories of positive hyperoctant trigonometric polynomials (PhTP). Our theoretical analyses show that the minimum number of samples and antennas required for perfect recovery is logarithmically dependent on the maximum of the number of radar targets and communications paths rather than their sum. We show that our approach is easily generalized to include several practical issues such as gain/phase errors and additive noise. Numerical experiments show the exact parameter recovery for different JRC