Stochastic Generative Plug-and-Play Priors

Plug-and-play (PnP) methods are widely used for solving imaging inverse problems by incorporating a denoiser into optimization algorithms. Score-based diffusion models (SBDMs) have recently demonstrated strong generative performance through a denoiser trained across a wide range of noise levels. Despite their shared reliance on denoisers, it remains unclear how to systematically use SBDMs as priors within the PnP framework without relying on reverse diffusion sampling. In this paper, we establish a score-based interpretation of PnP that justifies using pretrained SBDMs directly within PnP algorithms. Building on this connection, we introduce a stochastic generative PnP (SGPnP) framework that injects noise to better leverage the expressive generative SBDM priors, thereby improving robustness in severely ill-posed inverse problems. We provide a new theory showing that this noise injection induces optimization on a Gaussian-smoothed objective and promotes escape from strict saddle points. Experiments on challenging inverse tasks, such as multi-coil MRI reconstruction and large-mask natural image inpainting, demonstrate consistent improvement over conventional PnP methods and achieve performance competitive with diffusion-based solvers.

Material Identification using Multi-Modal Intrinsic Radiation and Radiography

We investigate multi-modal material identification for special nuclear material (SNM) configurations using a combination of X-ray radiography, high-resolution γ-ray spectroscopy, and neutron multiplicity measurements. We consider a Beryllium Reflected Plutonium sphere (BeRP) ball surrounded by one or two concentric shielding shells of unknown composition whose radii are assumed known from radiography. High-purity germanium (HPGe) spectra are reduced to net counts in selected Pu-239 photo-peaks, while neutron multiplicity information is summarized by Feynman variances Y2 and Y3 computed from factorial moments of the neutron counting statistics. Using synthetic data generated with the Gamma Detector Response and Analysis Software (GADRAS) for a range of shielding materials and thicknesses, we cast the material identification problem as a supervised multi-class classification task over all admissible shell-material combinations. We demonstrate that a random forest classifier trained on combined gamma and neutron features achieves almost perfect identification accuracy for single-shell cases, and substantial performance gains for more challenging double-shell configurations relative to gamma-only classification. Alternative statistical and machine-learning formulations for this multi-class problem are examined along with examination of the impact of model-mismatch between the forward model and the test cases as given by variations in the statistical noise. Opportunities for extending the approach to more complex geometries and experimental data are also discussed.

Analysis Plug-and-Play Methods for Imaging Inverse Problems

Plug-and-Play Priors (PnP) is a popular framework for solving imaging inverse problems by integrating learned priors in the form of denoisers trained to remove Gaussian noise from images. In standard PnP methods, the denoiser is applied directly in the image domain, serving as an implicit prior on natural images. This paper considers an alternative analysis formulation of PnP, in which the prior is imposed on a transformed representation of the image, such as its gradient. Specifically, we train a Gaussian denoiser to operate in the gradient domain, rather than on the image itself. Conceptually, this is an extension of total variation (TV) regularization to learned TV regularization. To incorporate this gradient-domain prior in image reconstruction algorithms, we develop two analysis PnP algorithms based on half-quadratic splitting (APnP-HQS) and the alternating direction method of multipliers (APnP-ADMM). We evaluate our approach on image deblurring and super-resolution, demonstrating that the analysis formulation achieves performance comparable to image-domain PnP algorithms.

An Adaptive Multiparameter Penalty Selection Method for Multiconstraint and Multiblock ADMM

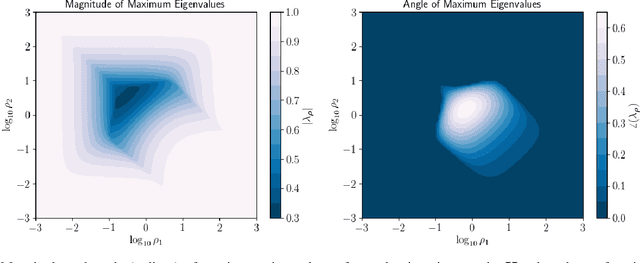
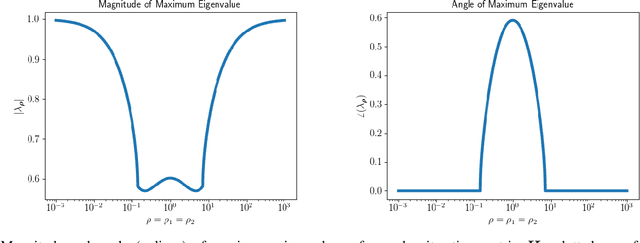
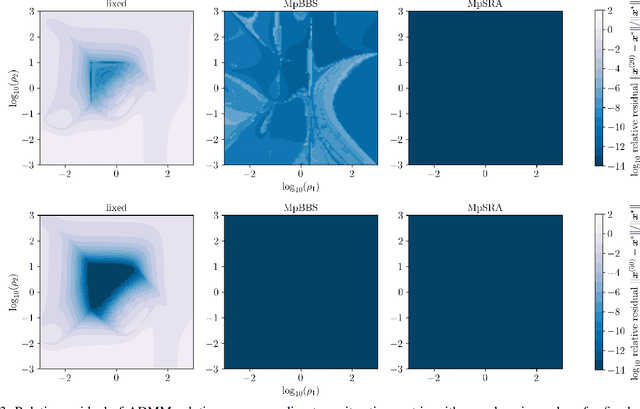
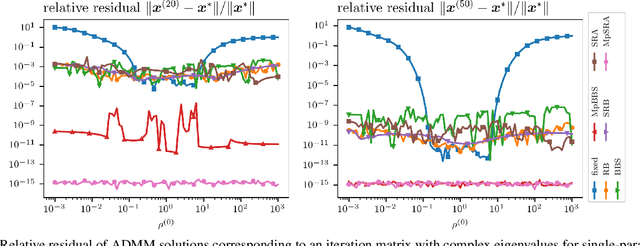
This work presents a new method for online selection of multiple penalty parameters for the alternating direction method of multipliers (ADMM) algorithm applied to optimization problems with multiple constraints or functionals with block matrix components. ADMM is widely used for solving constrained optimization problems in a variety of fields, including signal and image processing. Implementations of ADMM often utilize a single hyperparameter, referred to as the penalty parameter, which needs to be tuned to control the rate of convergence. However, in problems with multiple constraints, ADMM may demonstrate slow convergence regardless of penalty parameter selection due to scale differences between constraints. Accounting for scale differences between constraints to improve convergence in these cases requires introducing a penalty parameter for each constraint. The proposed method is able to adaptively account for differences in scale between constraints, providing robustness with respect to problem transformations and initial selection of penalty parameters. It is also simple to understand and implement. Our numerical experiments demonstrate that the proposed method performs favorably compared to a variety of existing penalty parameter selection methods.

Learned Correction Methods for Ultrasound Computed Tomography Imaging Using Simplified Physics Models

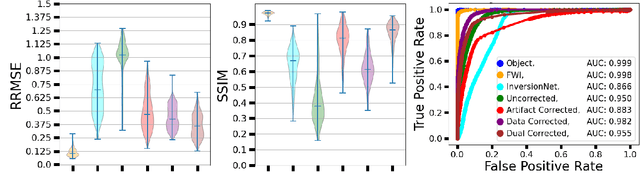
Ultrasound computed tomography (USCT) is an emerging modality for breast imaging. Image reconstruction methods that incorporate accurate wave physics produce high resolution quantitative images of acoustic properties but are computationally expensive. The use of a simplified linear model in reconstruction reduces computational expense at the cost of reduced accuracy. This work aims to systematically compare different learning approaches for USCT reconstruction utilizing simplified linear models. This work considered various learning approaches to compensate for errors stemming from a linearized wave propagation model: correction in the data and image domains. The resulting image reconstruction methods are systematically assessed, alongside data-driven and model-based methods, in four virtual imaging studies utilizing anatomically realistic numerical phantoms. Image quality was assessed utilizing relative root mean square error (RRMSE), structural similarity index measure (SSIM), and a task-based assessment for tumor detection. Correction in the measurement domain resulted in images with minor visual artifacts and highly accurate task performance. Correction in the image domain demonstrated a heavy bias on training data, resulting in hallucinations, but greater robustness to measurement noise. Combining both forms of correction performed best in terms of RRMSE and SSIM, at the cost of task performance. This work systematically assessed learned reconstruction methods incorporating an approximated physical model for USCT imaging. Results demonstrated the importance of incorporating physics, compared to data-driven methods. Learning a correction in the data domain led to better task performance and robust out-of-distribution generalization compared to correction in the image domain.

Ptychography using Blind Multi-Mode PMACE

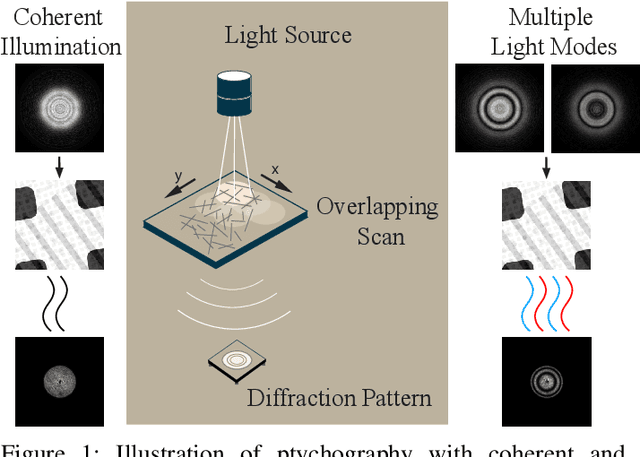
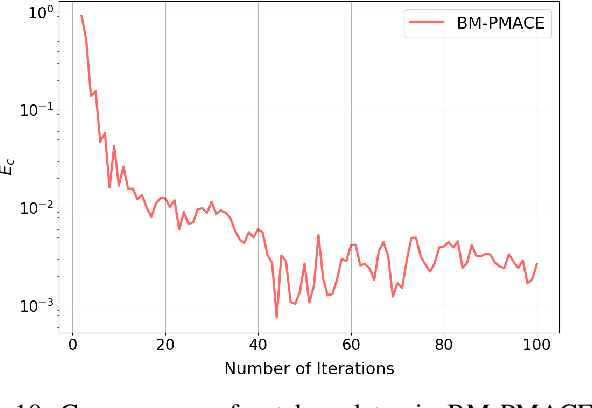
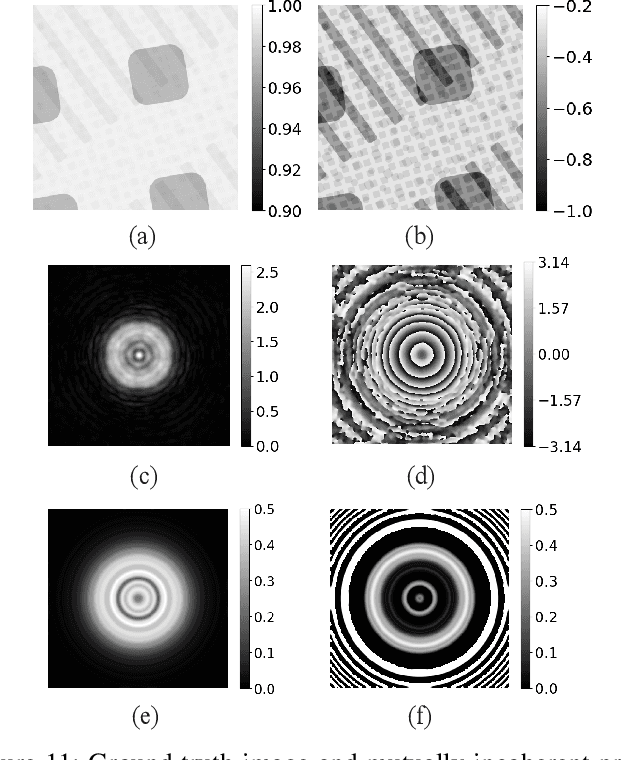
Ptychography is an imaging technique that enables nanometer-scale reconstruction of complex transmittance images by scanning objects with overlapping illumination patterns. However, the illumination function is typically unknown, which presents challenges for reconstruction, especially when using partially coherent light sources. In this paper, we introduce Blind Multi-Mode Projected Multi-Agent Consensus Equilibrium (BM-PMACE) for blind ptychographic reconstruction. We extend the PMACE framework for distributed inverse problems to jointly estimate the complex transmittance image and multiple, unknown, partially coherent probe functions. Importantly, our method maintains local probe estimates to exploit complementary information at multiple probe locations. Our method also incorporates a dynamic strategy for integrating additional probe modes. Through experimental simulations and validations using both synthetic and measured data, we demonstrate that BM-PMACE outperforms existing approaches in reconstruction quality and convergence rate.

Plug-and-Play Priors as a Score-Based Method

Plug-and-play (PnP) methods are extensively used for solving imaging inverse problems by integrating physical measurement models with pre-trained deep denoisers as priors. Score-based diffusion models (SBMs) have recently emerged as a powerful framework for image generation by training deep denoisers to represent the score of the image prior. While both PnP and SBMs use deep denoisers, the score-based nature of PnP is unexplored in the literature due to its distinct origins rooted in proximal optimization. This letter introduces a novel view of PnP as a score-based method, a perspective that enables the re-use of powerful SBMs within classical PnP algorithms without retraining. We present a set of mathematical relationships for adapting popular SBMs as priors within PnP. We show that this approach enables a direct comparison between PnP and SBM-based reconstruction methods using the same neural network as the prior. Code is available at https://github.com/wustl-cig/score_pnp.

Closed-Form Approximation of the Total Variation Proximal Operator

Total variation (TV) is a widely used function for regularizing imaging inverse problems that is particularly appropriate for images whose underlying structure is piecewise constant. TV regularized optimization problems are typically solved using proximal methods, but the way in which they are applied is constrained by the absence of a closed-form expression for the proximal operator of the TV function. A closed-form approximation of the TV proximal operator has previously been proposed, but its accuracy was not theoretically explored in detail. We address this gap by making several new theoretical contributions, proving that the approximation leads to a proximal operator of some convex function, that it always decreases the TV function, and that its error can be fully characterized and controlled with its scaling parameter. We experimentally validate our theoretical results on image denoising and sparse-view computed tomography (CT) image reconstruction.

Random Walks with Tweedie: A Unified Framework for Diffusion Models

We present a simple template for designing generative diffusion model algorithms based on an interpretation of diffusion sampling as a sequence of random walks. Score-based diffusion models are widely used to generate high-quality images. Diffusion models have also been shown to yield state-of-the-art performance in many inverse problems. While these algorithms are often surprisingly simple, the theory behind them is not, and multiple complex theoretical justifications exist in the literature. Here, we provide a simple and largely self-contained theoretical justification for score-based-diffusion models that avoids using the theory of Markov chains or reverse diffusion, instead centering the theory of random walks and Tweedie's formula. This approach leads to unified algorithmic templates for network training and sampling. In particular, these templates cleanly separate training from sampling, e.g., the noise schedule used during training need not match the one used during sampling. We show that several existing diffusion models correspond to particular choices within this template and demonstrate that other, more straightforward algorithmic choices lead to effective diffusion models. The proposed framework has the added benefit of enabling conditional sampling without any likelihood approximation.

Physics and Deep Learning in Computational Wave Imaging

Computational wave imaging (CWI) extracts hidden structure and physical properties of a volume of material by analyzing wave signals that traverse that volume. Applications include seismic exploration of the Earth's subsurface, acoustic imaging and non-destructive testing in material science, and ultrasound computed tomography in medicine. Current approaches for solving CWI problems can be divided into two categories: those rooted in traditional physics, and those based on deep learning. Physics-based methods stand out for their ability to provide high-resolution and quantitatively accurate estimates of acoustic properties within the medium. However, they can be computationally intensive and are susceptible to ill-posedness and nonconvexity typical of CWI problems. Machine learning-based computational methods have recently emerged, offering a different perspective to address these challenges. Diverse scientific communities have independently pursued the integration of deep learning in CWI. This review delves into how contemporary scientific machine-learning (ML) techniques, and deep neural networks in particular, have been harnessed to tackle CWI problems. We present a structured framework that consolidates existing research spanning multiple domains, including computational imaging, wave physics, and data science. This study concludes with important lessons learned from existing ML-based methods and identifies technical hurdles and emerging trends through a systematic analysis of the extensive literature on this topic.