Cristina Garcia-Cardona
Division of Computer, Computational and Statistical Sciences, Los Alamos National Laboratory, Los Alamos, NM, USA
A General Framework for Group Sparsity in Hyperspectral Unmixing Using Endmember Bundles
May 20, 2025Abstract:Due to low spatial resolution, hyperspectral data often consists of mixtures of contributions from multiple materials. This limitation motivates the task of hyperspectral unmixing (HU), a fundamental problem in hyperspectral imaging. HU aims to identify the spectral signatures (\textit{endmembers}) of the materials present in an observed scene, along with their relative proportions (\textit{fractional abundance}) in each pixel. A major challenge lies in the class variability in materials, which hinders accurate representation by a single spectral signature, as assumed in the conventional linear mixing model. Moreover, To address this issue, we propose using group sparsity after representing each material with a set of spectral signatures, known as endmember bundles, where each group corresponds to a specific material. In particular, we develop a bundle-based framework that can enforce either inter-group sparsity or sparsity within and across groups (SWAG) on the abundance coefficients. Furthermore, our framework offers the flexibility to incorporate a variety of sparsity-promoting penalties, among which the transformed $\ell_1$ (TL1) penalty is a novel regularization in the HU literature. Extensive experiments conducted on both synthetic and real hyperspectral data demonstrate the effectiveness and superiority of the proposed approaches.
Benchmarking community drug response prediction models: datasets, models, tools, and metrics for cross-dataset generalization analysis
Mar 18, 2025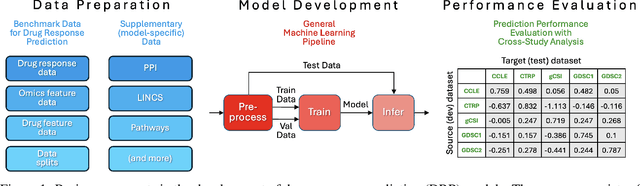
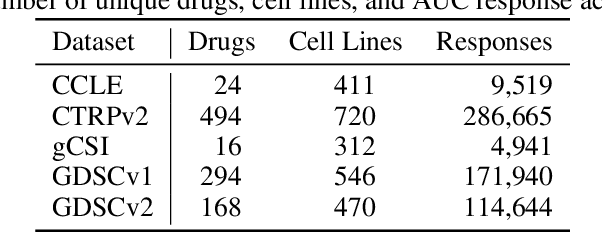
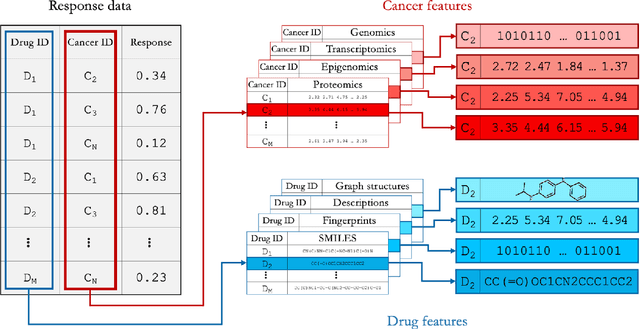

Abstract:Deep learning (DL) and machine learning (ML) models have shown promise in drug response prediction (DRP), yet their ability to generalize across datasets remains an open question, raising concerns about their real-world applicability. Due to the lack of standardized benchmarking approaches, model evaluations and comparisons often rely on inconsistent datasets and evaluation criteria, making it difficult to assess true predictive capabilities. In this work, we introduce a benchmarking framework for evaluating cross-dataset prediction generalization in DRP models. Our framework incorporates five publicly available drug screening datasets, six standardized DRP models, and a scalable workflow for systematic evaluation. To assess model generalization, we introduce a set of evaluation metrics that quantify both absolute performance (e.g., predictive accuracy across datasets) and relative performance (e.g., performance drop compared to within-dataset results), enabling a more comprehensive assessment of model transferability. Our results reveal substantial performance drops when models are tested on unseen datasets, underscoring the importance of rigorous generalization assessments. While several models demonstrate relatively strong cross-dataset generalization, no single model consistently outperforms across all datasets. Furthermore, we identify CTRPv2 as the most effective source dataset for training, yielding higher generalization scores across target datasets. By sharing this standardized evaluation framework with the community, our study aims to establish a rigorous foundation for model comparison, and accelerate the development of robust DRP models for real-world applications.
Plug-and-Play Priors as a Score-Based Method
Dec 15, 2024Abstract:Plug-and-play (PnP) methods are extensively used for solving imaging inverse problems by integrating physical measurement models with pre-trained deep denoisers as priors. Score-based diffusion models (SBMs) have recently emerged as a powerful framework for image generation by training deep denoisers to represent the score of the image prior. While both PnP and SBMs use deep denoisers, the score-based nature of PnP is unexplored in the literature due to its distinct origins rooted in proximal optimization. This letter introduces a novel view of PnP as a score-based method, a perspective that enables the re-use of powerful SBMs within classical PnP algorithms without retraining. We present a set of mathematical relationships for adapting popular SBMs as priors within PnP. We show that this approach enables a direct comparison between PnP and SBM-based reconstruction methods using the same neural network as the prior. Code is available at https://github.com/wustl-cig/score_pnp.
Random Walks with Tweedie: A Unified Framework for Diffusion Models
Nov 27, 2024Abstract:We present a simple template for designing generative diffusion model algorithms based on an interpretation of diffusion sampling as a sequence of random walks. Score-based diffusion models are widely used to generate high-quality images. Diffusion models have also been shown to yield state-of-the-art performance in many inverse problems. While these algorithms are often surprisingly simple, the theory behind them is not, and multiple complex theoretical justifications exist in the literature. Here, we provide a simple and largely self-contained theoretical justification for score-based-diffusion models that avoids using the theory of Markov chains or reverse diffusion, instead centering the theory of random walks and Tweedie's formula. This approach leads to unified algorithmic templates for network training and sampling. In particular, these templates cleanly separate training from sampling, e.g., the noise schedule used during training need not match the one used during sampling. We show that several existing diffusion models correspond to particular choices within this template and demonstrate that other, more straightforward algorithmic choices lead to effective diffusion models. The proposed framework has the added benefit of enabling conditional sampling without any likelihood approximation.
Uncertainty Bounds for Multivariate Machine Learning Predictions on High-Strain Brittle Fracture
Dec 23, 2020
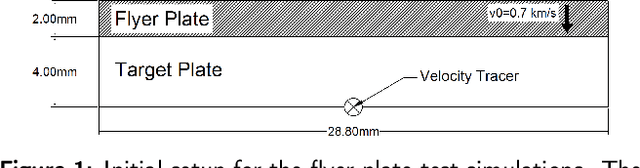


Abstract:Simulation of the crack network evolution on high strain rate impact experiments performed in brittle materials is very compute-intensive. The cost increases even more if multiple simulations are needed to account for the randomness in crack length, location, and orientation, which is inherently found in real-world materials. Constructing a machine learning emulator can make the process faster by orders of magnitude. There has been little work, however, on assessing the error associated with their predictions. Estimating these errors is imperative for meaningful overall uncertainty quantification. In this work, we extend the heteroscedastic uncertainty estimates to bound a multiple output machine learning emulator. We find that the response prediction is robust with a somewhat conservative estimate of uncertainty.
Convolutional Dictionary Learning: A Comparative Review and New Algorithms
Sep 05, 2018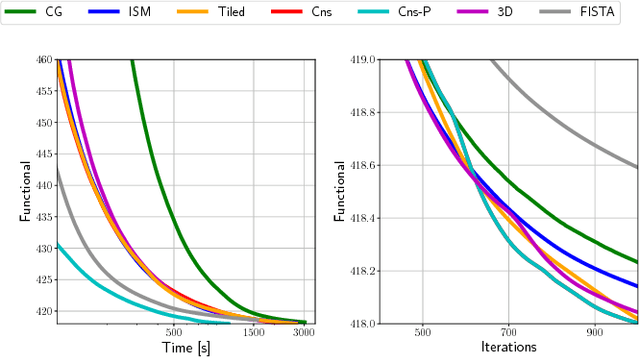
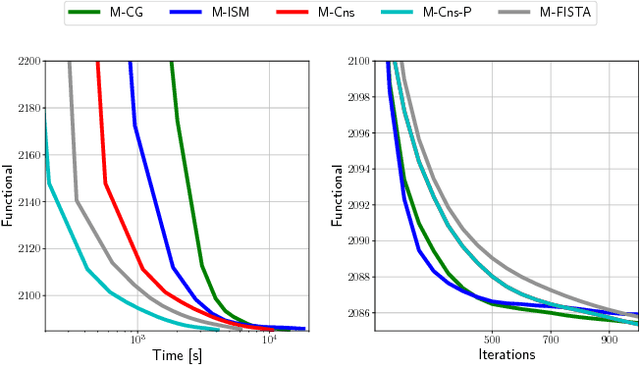
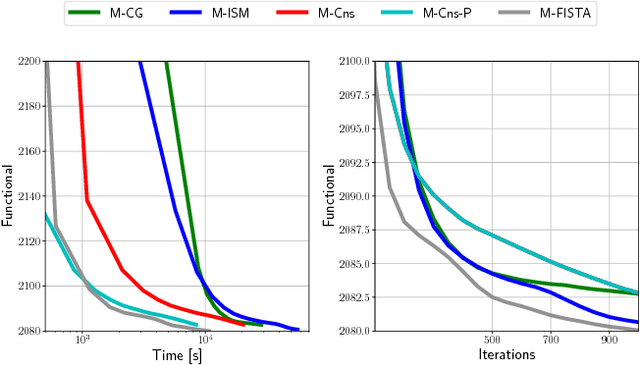
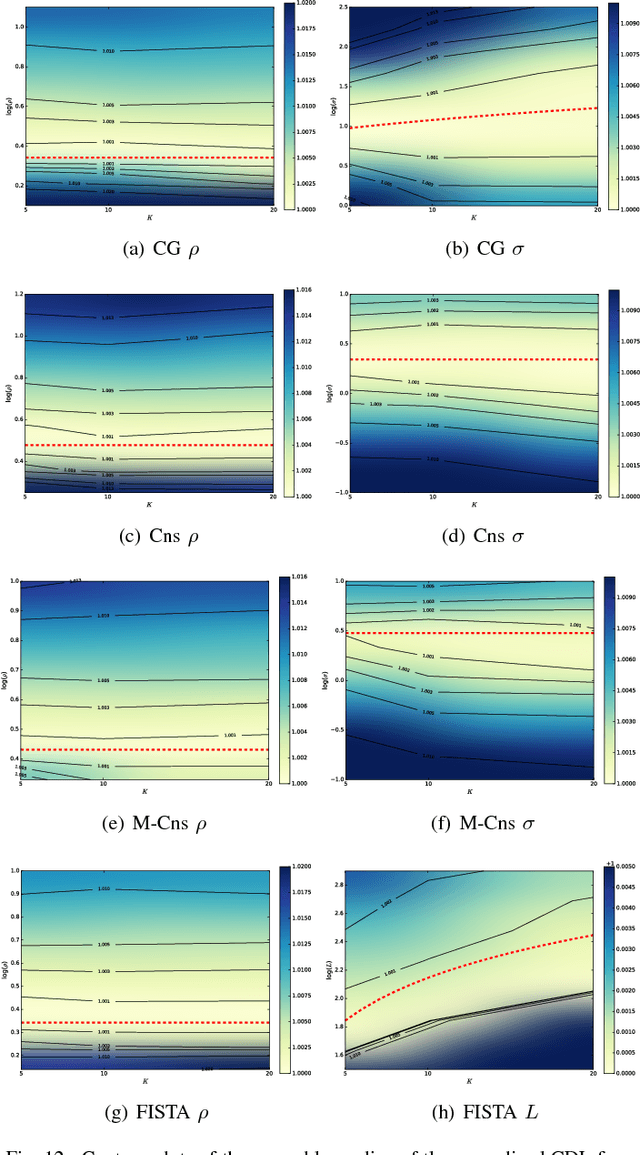
Abstract:Convolutional sparse representations are a form of sparse representation with a dictionary that has a structure that is equivalent to convolution with a set of linear filters. While effective algorithms have recently been developed for the convolutional sparse coding problem, the corresponding dictionary learning problem is substantially more challenging. Furthermore, although a number of different approaches have been proposed, the absence of thorough comparisons between them makes it difficult to determine which of them represents the current state of the art. The present work both addresses this deficiency and proposes some new approaches that outperform existing ones in certain contexts. A thorough set of performance comparisons indicates a very wide range of performance differences among the existing and proposed methods, and clearly identifies those that are the most effective.
* Corrected typos in Eq. (18) and (19)
Online Convolutional Dictionary Learning
Aug 30, 2017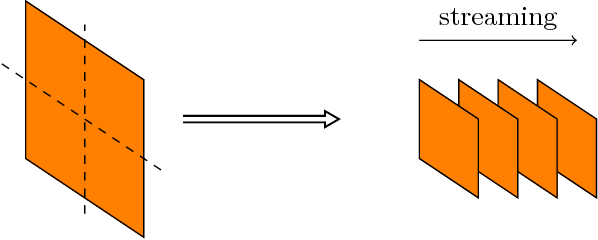

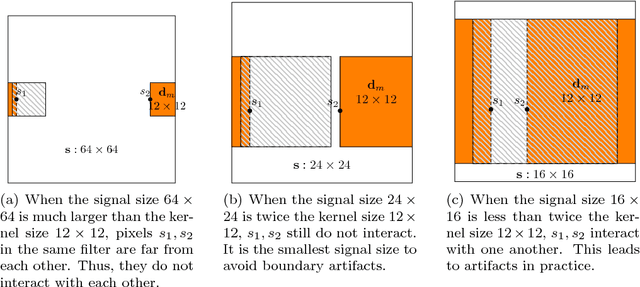
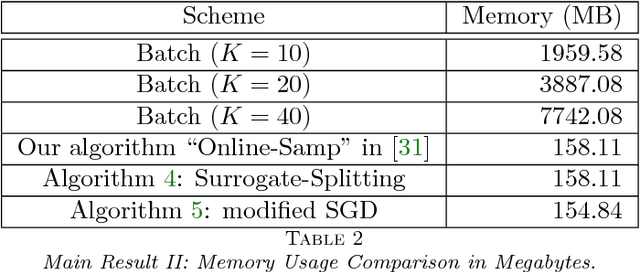
Abstract:While a number of different algorithms have recently been proposed for convolutional dictionary learning, this remains an expensive problem. The single biggest impediment to learning from large training sets is the memory requirements, which grow at least linearly with the size of the training set since all existing methods are batch algorithms. The work reported here addresses this limitation by extending online dictionary learning ideas to the convolutional context.
* Accepted to be presented at ICIP 2017
Multiclass Data Segmentation using Diffuse Interface Methods on Graphs
Jan 17, 2014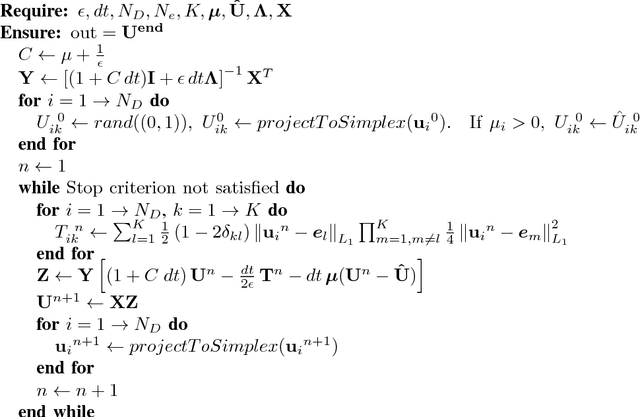
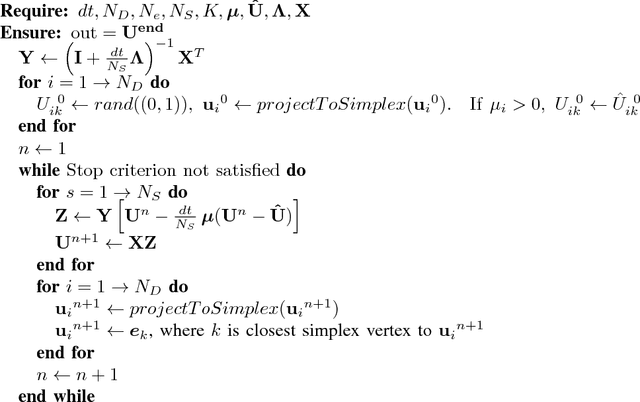

Abstract:We present two graph-based algorithms for multiclass segmentation of high-dimensional data. The algorithms use a diffuse interface model based on the Ginzburg-Landau functional, related to total variation compressed sensing and image processing. A multiclass extension is introduced using the Gibbs simplex, with the functional's double-well potential modified to handle the multiclass case. The first algorithm minimizes the functional using a convex splitting numerical scheme. The second algorithm is a uses a graph adaptation of the classical numerical Merriman-Bence-Osher (MBO) scheme, which alternates between diffusion and thresholding. We demonstrate the performance of both algorithms experimentally on synthetic data, grayscale and color images, and several benchmark data sets such as MNIST, COIL and WebKB. We also make use of fast numerical solvers for finding the eigenvectors and eigenvalues of the graph Laplacian, and take advantage of the sparsity of the matrix. Experiments indicate that the results are competitive with or better than the current state-of-the-art multiclass segmentation algorithms.
Spectral Clustering with Epidemic Diffusion
Oct 04, 2013
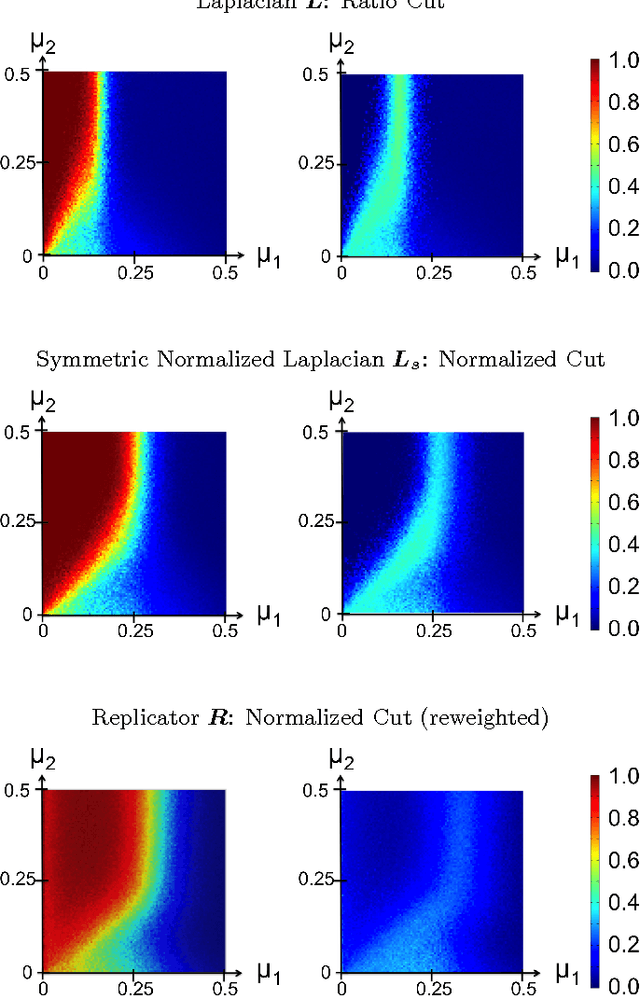
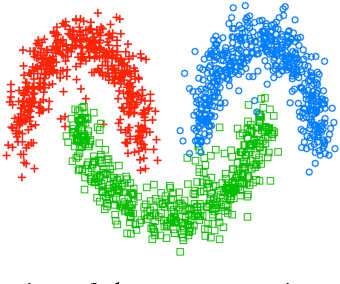
Abstract:Spectral clustering is widely used to partition graphs into distinct modules or communities. Existing methods for spectral clustering use the eigenvalues and eigenvectors of the graph Laplacian, an operator that is closely associated with random walks on graphs. We propose a new spectral partitioning method that exploits the properties of epidemic diffusion. An epidemic is a dynamic process that, unlike the random walk, simultaneously transitions to all the neighbors of a given node. We show that the replicator, an operator describing epidemic diffusion, is equivalent to the symmetric normalized Laplacian of a reweighted graph with edges reweighted by the eigenvector centralities of their incident nodes. Thus, more weight is given to edges connecting more central nodes. We describe a method that partitions the nodes based on the componentwise ratio of the replicator's second eigenvector to the first, and compare its performance to traditional spectral clustering techniques on synthetic graphs with known community structure. We demonstrate that the replicator gives preference to dense, clique-like structures, enabling it to more effectively discover communities that may be obscured by dense intercommunity linking.
Multiclass Semi-Supervised Learning on Graphs using Ginzburg-Landau Functional Minimization
Jun 06, 2013


Abstract:We present a graph-based variational algorithm for classification of high-dimensional data, generalizing the binary diffuse interface model to the case of multiple classes. Motivated by total variation techniques, the method involves minimizing an energy functional made up of three terms. The first two terms promote a stepwise continuous classification function with sharp transitions between classes, while preserving symmetry among the class labels. The third term is a data fidelity term, allowing us to incorporate prior information into the model in a semi-supervised framework. The performance of the algorithm on synthetic data, as well as on the COIL and MNIST benchmark datasets, is competitive with state-of-the-art graph-based multiclass segmentation methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge