In-Group Love, Out-Group Hate: A Framework to Measure Affective Polarization via Contentious Online Discussions

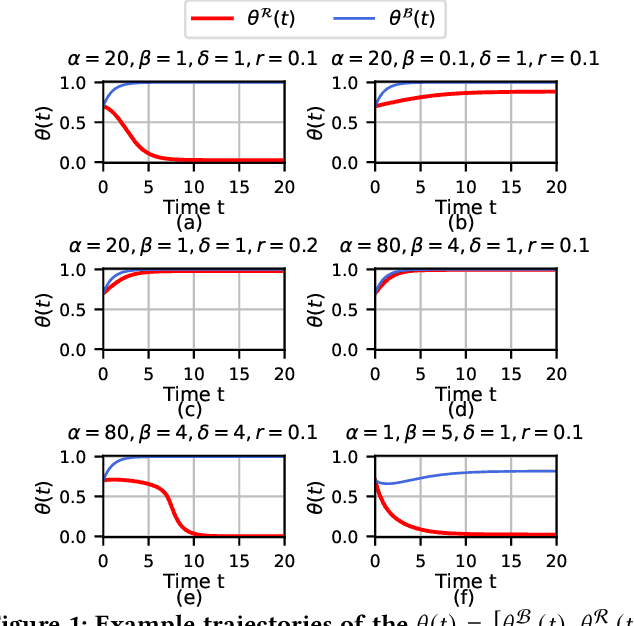
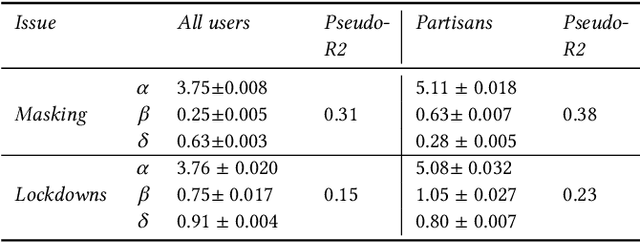
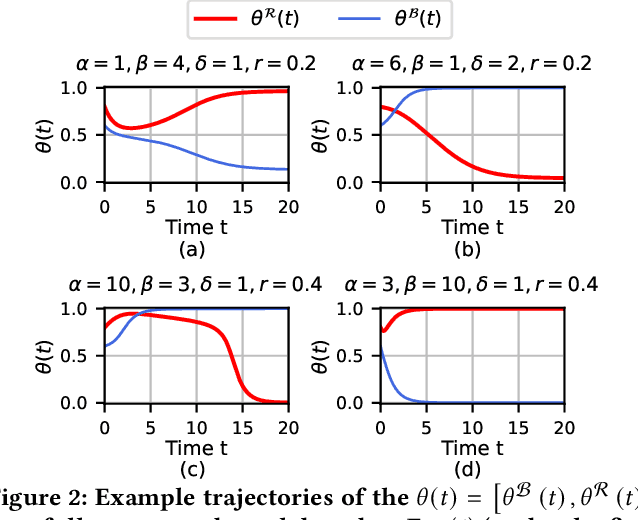
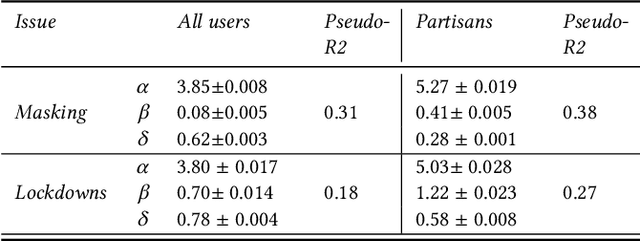
Affective polarization, the emotional divide between ideological groups marked by in-group love and out-group hate, has intensified in the United States, driving contentious issues like masking and lockdowns during the COVID-19 pandemic. Despite its societal impact, existing models of opinion change fail to account for emotional dynamics nor offer methods to quantify affective polarization robustly and in real-time. In this paper, we introduce a discrete choice model that captures decision-making within affectively polarized social networks and propose a statistical inference method estimate key parameters -- in-group love and out-group hate -- from social media data. Through empirical validation from online discussions about the COVID-19 pandemic, we demonstrate that our approach accurately captures real-world polarization dynamics and explains the rapid emergence of a partisan gap in attitudes towards masking and lockdowns. This framework allows for tracking affective polarization across contentious issues has broad implications for fostering constructive online dialogues in digital spaces.

Multiclass Data Segmentation using Diffuse Interface Methods on Graphs

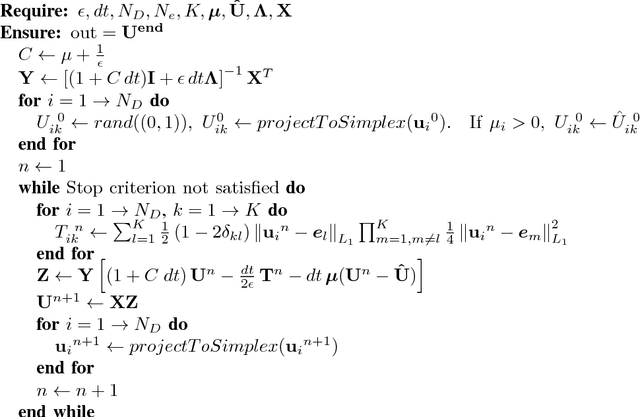
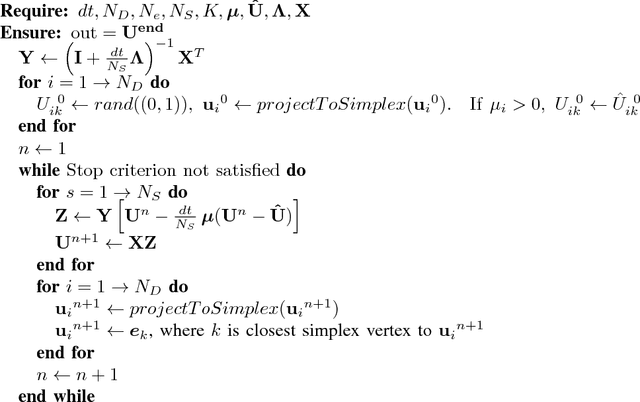
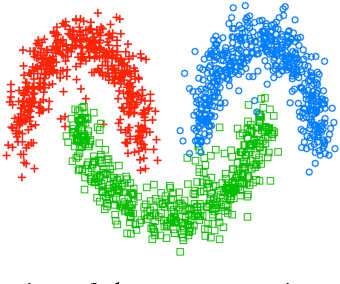
We present two graph-based algorithms for multiclass segmentation of high-dimensional data. The algorithms use a diffuse interface model based on the Ginzburg-Landau functional, related to total variation compressed sensing and image processing. A multiclass extension is introduced using the Gibbs simplex, with the functional's double-well potential modified to handle the multiclass case. The first algorithm minimizes the functional using a convex splitting numerical scheme. The second algorithm is a uses a graph adaptation of the classical numerical Merriman-Bence-Osher (MBO) scheme, which alternates between diffusion and thresholding. We demonstrate the performance of both algorithms experimentally on synthetic data, grayscale and color images, and several benchmark data sets such as MNIST, COIL and WebKB. We also make use of fast numerical solvers for finding the eigenvectors and eigenvalues of the graph Laplacian, and take advantage of the sparsity of the matrix. Experiments indicate that the results are competitive with or better than the current state-of-the-art multiclass segmentation algorithms.