In-Group Love, Out-Group Hate: A Framework to Measure Affective Polarization via Contentious Online Discussions

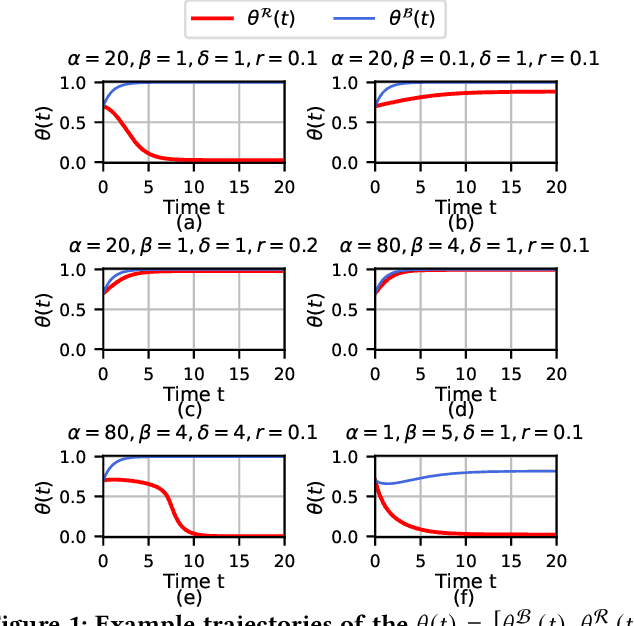
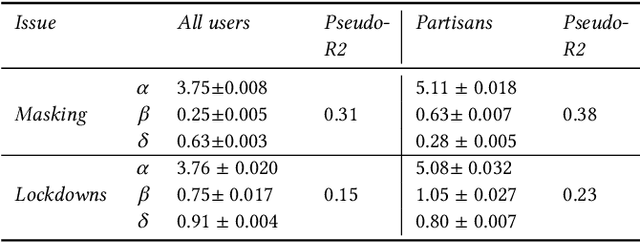
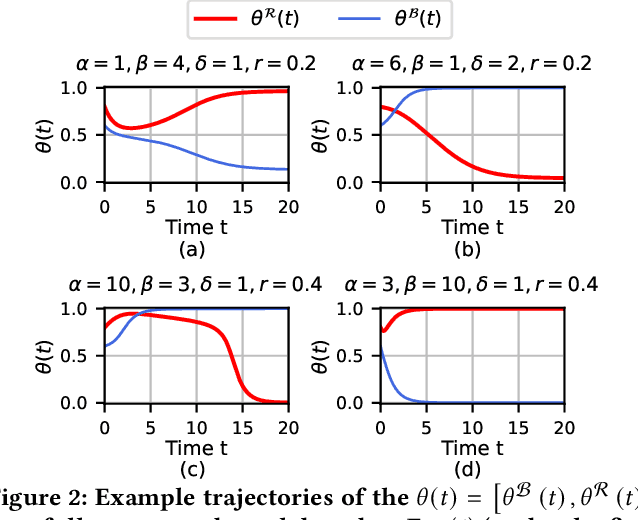
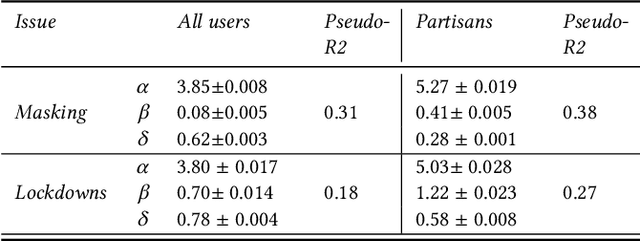
Affective polarization, the emotional divide between ideological groups marked by in-group love and out-group hate, has intensified in the United States, driving contentious issues like masking and lockdowns during the COVID-19 pandemic. Despite its societal impact, existing models of opinion change fail to account for emotional dynamics nor offer methods to quantify affective polarization robustly and in real-time. In this paper, we introduce a discrete choice model that captures decision-making within affectively polarized social networks and propose a statistical inference method estimate key parameters -- in-group love and out-group hate -- from social media data. Through empirical validation from online discussions about the COVID-19 pandemic, we demonstrate that our approach accurately captures real-world polarization dynamics and explains the rapid emergence of a partisan gap in attitudes towards masking and lockdowns. This framework allows for tracking affective polarization across contentious issues has broad implications for fostering constructive online dialogues in digital spaces.

Extending Conformal Prediction to Hidden Markov Models with Exact Validity via de Finetti's Theorem for Markov Chains

Conformal prediction is a widely used method to quantify uncertainty in settings where the data is independent and identically distributed (IID), or more generally, exchangeable. Conformal prediction takes in a pre-trained classifier, a calibration dataset and a confidence level as inputs, and returns a function which maps feature vectors to subsets of classes. The output of the returned function for a new feature vector (i.e., a test data point) is guaranteed to contain the true class with the pre-specified confidence. Despite its success and usefulness in IID settings, extending conformal prediction to non-exchangeable (e.g., Markovian) data in a manner that provably preserves all desirable theoretical properties has largely remained an open problem. As a solution, we extend conformal prediction to the setting of a Hidden Markov Model (HMM) with unknown parameters. The key idea behind the proposed method is to partition the non-exchangeable Markovian data from the HMM into exchangeable blocks by exploiting the de Finetti's Theorem for Markov Chains discovered by Diaconis and Freedman (1980). The permutations of the exchangeable blocks are then viewed as randomizations of the observed Markovian data from the HMM. The proposed method provably retains all desirable theoretical guarantees offered by the classical conformal prediction framework and is general enough to be useful in many sequential prediction problems.

Estimating Exposure to Information on Social Networks

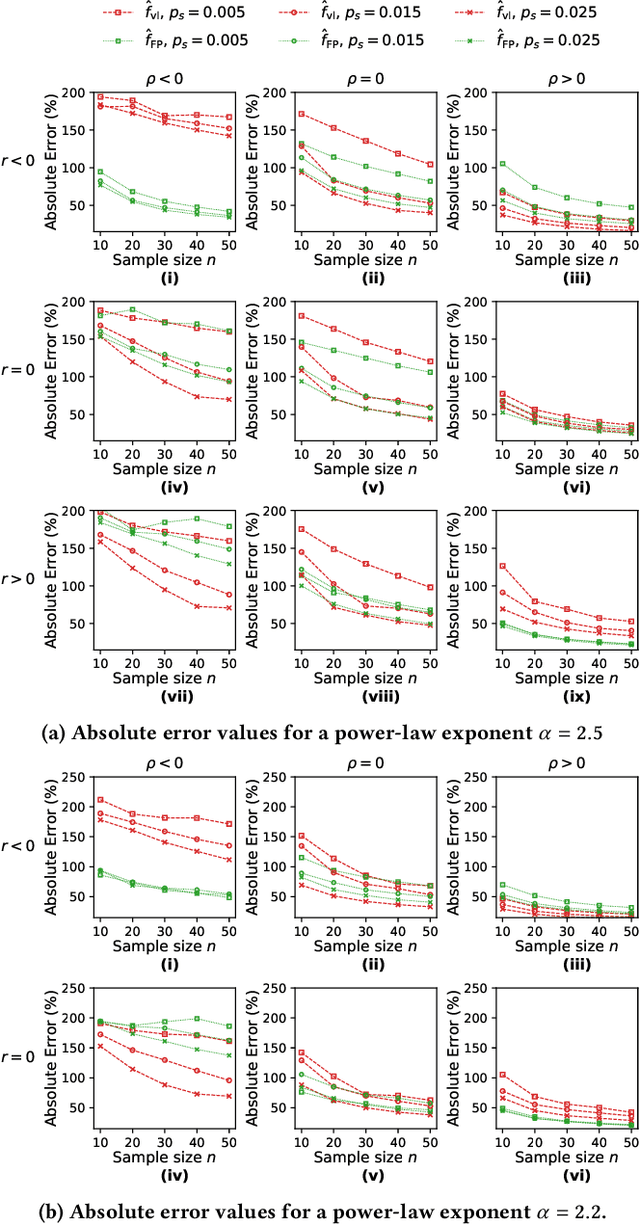
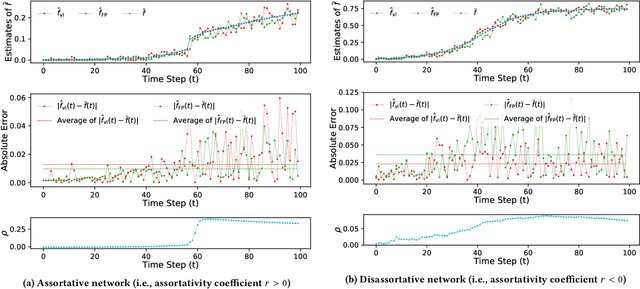
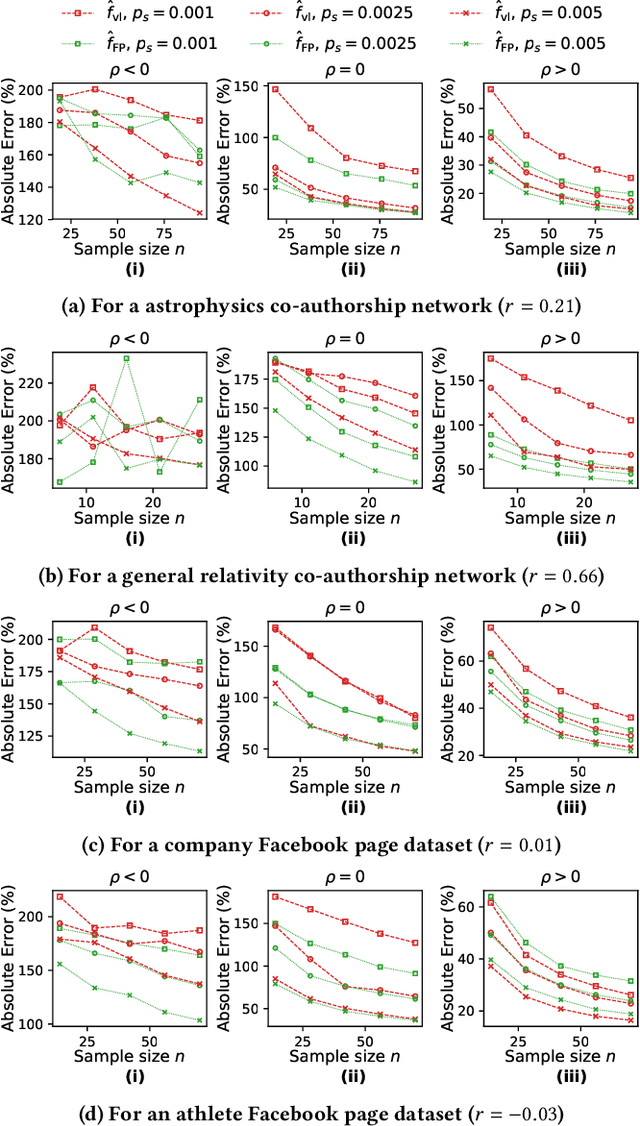
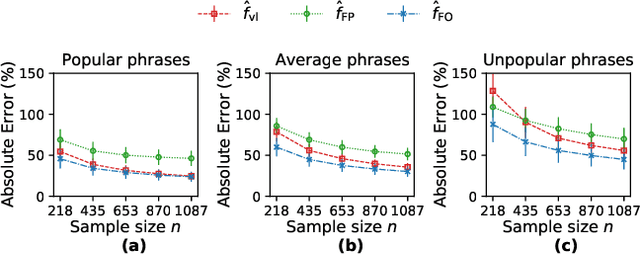
This paper considers the problem of estimating exposure to information in a social network. Given a piece of information (e.g., a URL of a news article on Facebook, a hashtag on Twitter), our aim is to find the fraction of people on the network who have been exposed to it. The exact value of exposure to a piece of information is determined by two features: the structure of the underlying social network and the set of people who shared the piece of information. Often, both features are not publicly available (i.e., access to the two features is limited only to the internal administrators of the platform) and difficult to be estimated from data. As a solution, we propose two methods to estimate the exposure to a piece of information in an unbiased manner: a vanilla method which is based on sampling the network uniformly and a method which non-uniformly samples the network motivated by the Friendship Paradox. We provide theoretical results which characterize the conditions (in terms of properties of the network and the piece of information) under which one method outperforms the other. Further, we outline extensions of the proposed methods to dynamic information cascades (where the exposure needs to be tracked in real-time). We demonstrate the practical feasibility of the proposed methods via experiments on multiple synthetic and real-world datasets.

Anomalous Edge Detection in Edge Exchangeable Social Network Models

This paper studies detecting anomalous edges in directed graphs that model social networks. We exploit edge exchangeability as a criterion for distinguishing anomalous edges from normal edges. Then we present an anomaly detector based on conformal prediction theory; this detector has a guaranteed upper bound for false positive rate. In numerical experiments, we show that the proposed algorithm achieves superior performance to baseline methods.

Echo Chambers and Segregation in Social Networks: Markov Bridge Models and Estimation

This paper deals with the modeling and estimation of the sociological phenomena called echo chambers and segregation in social networks. Specifically, we present a novel community-based graph model that represents the emergence of segregated echo chambers as a Markov bridge process. A Markov bridge is a one-dimensional Markov random field that facilitates modeling the formation and disassociation of communities at deterministic times which is important in social networks with known timed events. We justify the proposed model with six real world examples and examine its performance on a recent Twitter dataset. We provide model parameter estimation algorithm based on maximum likelihood and, a Bayesian filtering algorithm for recursively estimating the level of segregation using noisy samples obtained from the network. Numerical results indicate that the proposed filtering algorithm outperforms the conventional hidden Markov modeling in terms of the mean-squared error. The proposed filtering method is useful in computational social science where data-driven estimation of the level of segregation from noisy data is required.