Conditional Korhunen-Loéve regression model with Basis Adaptation for high-dimensional problems: uncertainty quantification and inverse modeling

We propose a methodology for improving the accuracy of surrogate models of the observable response of physical systems as a function of the systems' spatially heterogeneous parameter fields with applications to uncertainty quantification and parameter estimation in high-dimensional problems. Practitioners often formulate finite-dimensional representations of spatially heterogeneous parameter fields using truncated unconditional Karhunen-Lo\'{e}ve expansions (KLEs) for a certain choice of unconditional covariance kernel and construct surrogate models of the observable response with respect to the random variables in the KLE. When direct measurements of the parameter fields are available, we propose improving the accuracy of these surrogate models by representing the parameter fields via conditional Karhunen-Lo\'{e}ve expansions (CKLEs). CKLEs are constructed by conditioning the covariance kernel of the unconditional expansion on the direct measurements via Gaussian process regression and then truncating the corresponding KLE. We apply the proposed methodology to constructing surrogate models via the Basis Adaptation (BA) method of the stationary hydraulic head response, measured at spatially discrete observation locations, of a groundwater flow model of the Hanford Site, as a function of the 1,000-dimensional representation of the model's log-transmissivity field. We find that BA surrogate models of the hydraulic head based on CKLEs are more accurate than BA surrogate models based on unconditional expansions for forward uncertainty quantification tasks. Furthermore, we find that inverse estimates of the hydraulic transmissivity field computed using CKLE-based BA surrogate models are more accurate than those computed using unconditional BA surrogate models.

Extending Conformal Prediction to Hidden Markov Models with Exact Validity via de Finetti's Theorem for Markov Chains

Conformal prediction is a widely used method to quantify uncertainty in settings where the data is independent and identically distributed (IID), or more generally, exchangeable. Conformal prediction takes in a pre-trained classifier, a calibration dataset and a confidence level as inputs, and returns a function which maps feature vectors to subsets of classes. The output of the returned function for a new feature vector (i.e., a test data point) is guaranteed to contain the true class with the pre-specified confidence. Despite its success and usefulness in IID settings, extending conformal prediction to non-exchangeable (e.g., Markovian) data in a manner that provably preserves all desirable theoretical properties has largely remained an open problem. As a solution, we extend conformal prediction to the setting of a Hidden Markov Model (HMM) with unknown parameters. The key idea behind the proposed method is to partition the non-exchangeable Markovian data from the HMM into exchangeable blocks by exploiting the de Finetti's Theorem for Markov Chains discovered by Diaconis and Freedman (1980). The permutations of the exchangeable blocks are then viewed as randomizations of the observed Markovian data from the HMM. The proposed method provably retains all desirable theoretical guarantees offered by the classical conformal prediction framework and is general enough to be useful in many sequential prediction problems.

Lorenz System State Stability Identification using Neural Networks

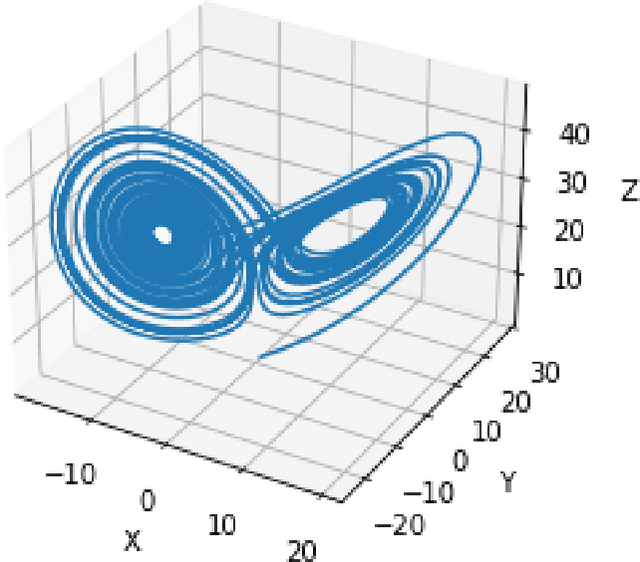
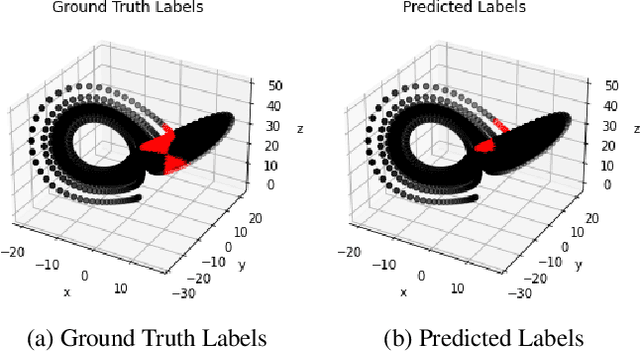
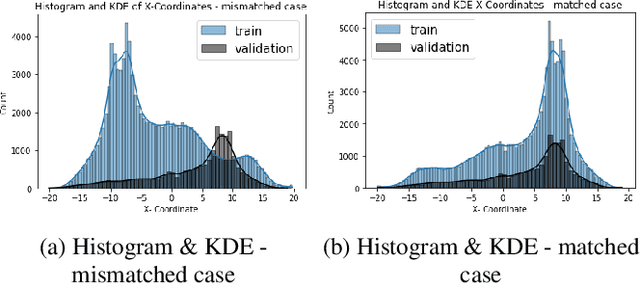
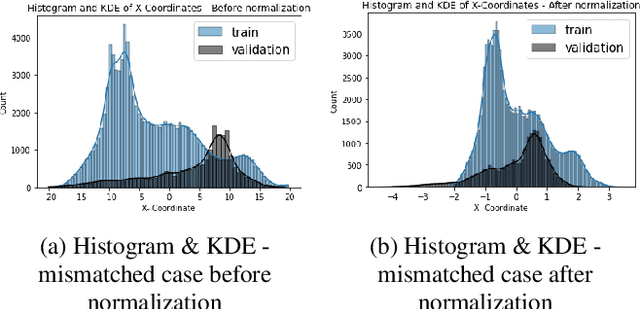
Nonlinear dynamical systems such as Lorenz63 equations are known to be chaotic in nature and sensitive to initial conditions. As a result, a small perturbation in the initial conditions results in deviation in state trajectory after a few time steps. The algorithms and computational resources needed to accurately identify the system states vary depending on whether the solution is in transition region or not. We refer to the transition and non-transition regions as unstable and stable regions respectively. We label a system state to be stable if it's immediate past and future states reside in the same regime. However, at a given time step we don't have the prior knowledge about whether system is in stable or unstable region. In this paper, we develop and train a feed forward (multi-layer perceptron) Neural Network to classify the system states of a Lorenz system as stable and unstable. We pose this task as a supervised learning problem where we train the neural network on Lorenz system which have states labeled as stable or unstable. We then test the ability of the neural network models to identify the stable and unstable states on a different Lorenz system that is generated using different initial conditions. We also evaluate the classification performance in the mismatched case i.e., when the initial conditions for training and validation data are sampled from different intervals. We show that certain normalization schemes can greatly improve the performance of neural networks in especially these mismatched scenarios. The classification framework developed in the paper can be a preprocessor for a larger context of sequential decision making framework where the decision making is performed based on observed stable or unstable states.

Physics-Informed Gaussian Process Regression for Probabilistic States Estimation and Forecasting in Power Grids

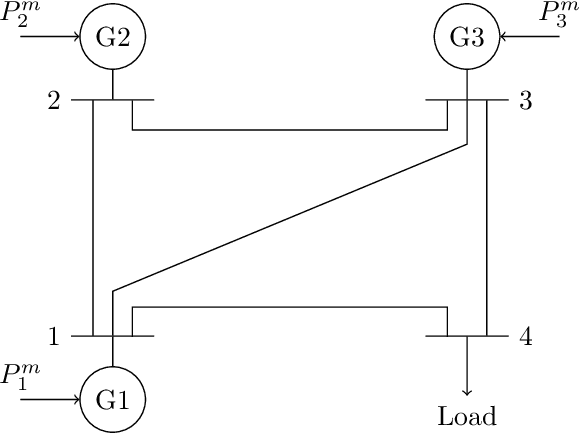
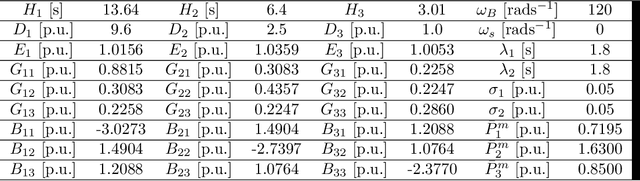
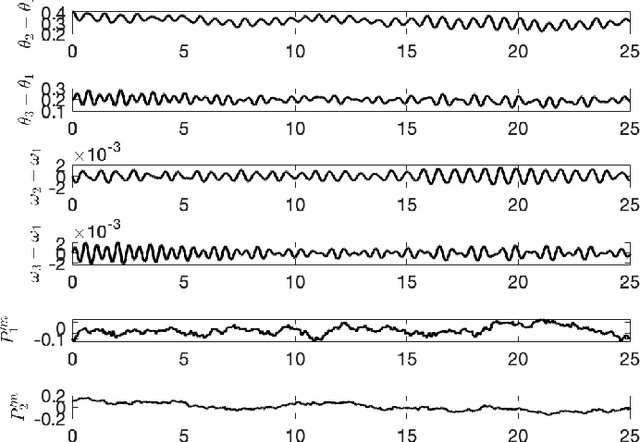
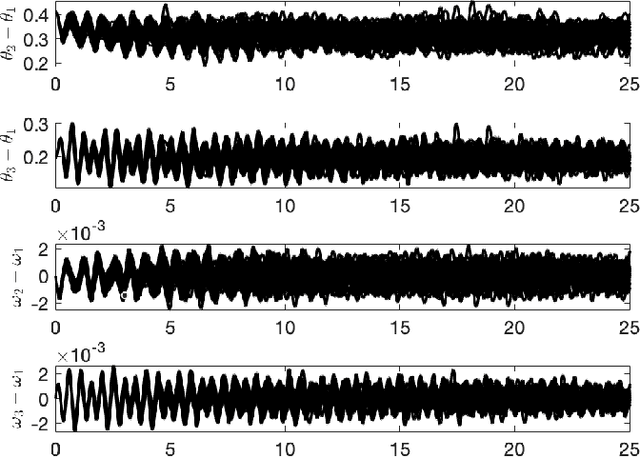
Real-time state estimation and forecasting is critical for efficient operation of power grids. In this paper, a physics-informed Gaussian process regression (PhI-GPR) method is presented and used for probabilistic forecasting and estimating the phase angle, angular speed, and wind mechanical power of a three-generator power grid system using sparse measurements. In standard data-driven Gaussian process regression (GPR), parameterized models for the prior statistics are fit by maximizing the marginal likelihood of observed data, whereas in PhI-GPR, we compute the prior statistics by solving stochastic equations governing power grid dynamics. The short-term forecast of a power grid system dominated by wind generation is complicated by the stochastic nature of the wind and the resulting uncertain mechanical wind power. Here, we assume that the power-grid dynamic is governed by the swing equations, and we treat the unknown terms in the swing equations (specifically, the mechanical wind power) as random processes, which turns these equations into stochastic differential equations. We solve these equations for the mean and variance of the power grid system using the Monte Carlo simulations method. We demonstrate that the proposed PhI-GPR method can accurately forecast and estimate both observed and unobserved states, including the mean behavior and associated uncertainty. For observed states, we show that PhI-GPR provides a forecast comparable to the standard data-driven GPR, with both forecasts being significantly more accurate than the autoregressive integrated moving average (ARIMA) forecast. We also show that the ARIMA forecast is much more sensitive to observation frequency and measurement errors than the PhI-GPR forecast.

Electric Load and Power Forecasting Using Ensemble Gaussian Process Regression

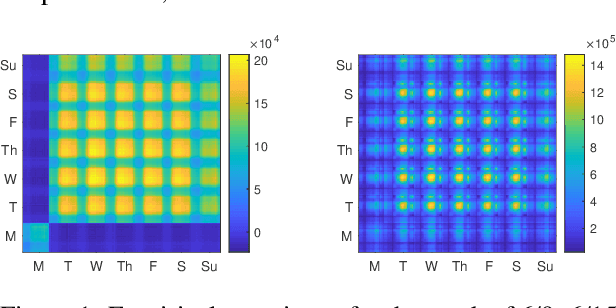
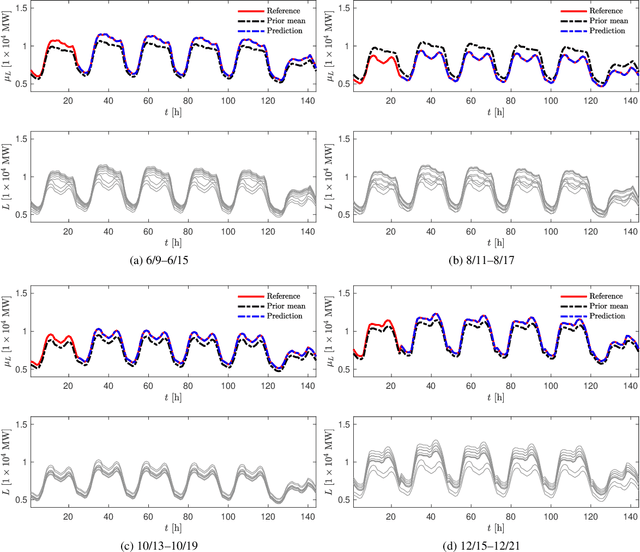
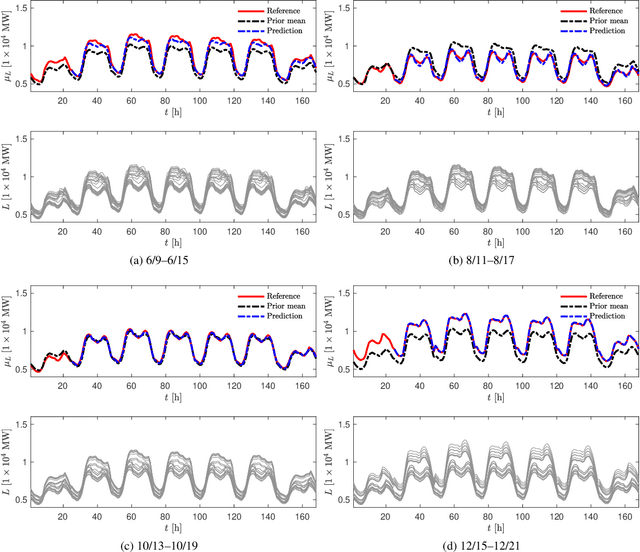
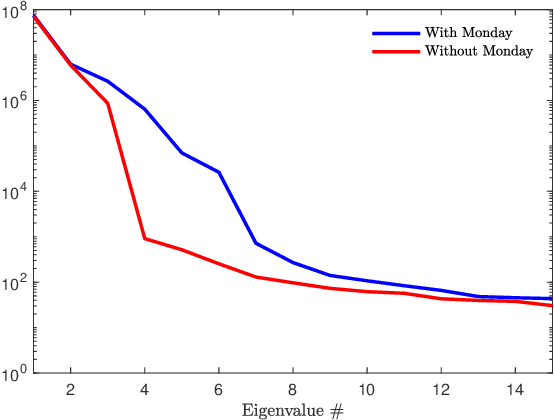
We propose a new forecasting method for predicting load demand and generation scheduling. Accurate week-long forecasting of load demand and optimal power generation is critical for efficient operation of power grid systems. In this work, we use a synthetic data set describing a power grid with 700 buses and 134 generators over a 365-days period with data synthetically generated at an hourly rate. The proposed approach for week-long forecasting is based on the Gaussian process regression (GPR) method, with prior covariance matrices of the quantities of interest (QoI) computed from ensembles formed by up to twenty preceding weeks of QoI observations. Then, we use these covariances within the GPR framework to forecast the QoIs for the following week. We demonstrate that the the proposed ensemble GPR (EGPR) method is capable of accurately forecasting weekly total load demand and power generation profiles. The EGPR method is shown to outperform traditional forecasting methods including the standard GPR and autoregressive integrated moving average (ARIMA) methods.

A comparative study of physics-informed neural network models for learning unknown dynamics and constitutive relations

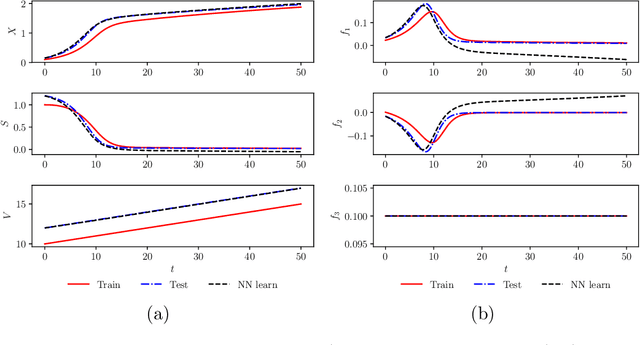
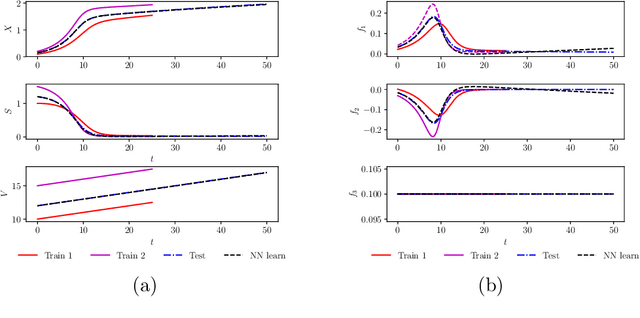
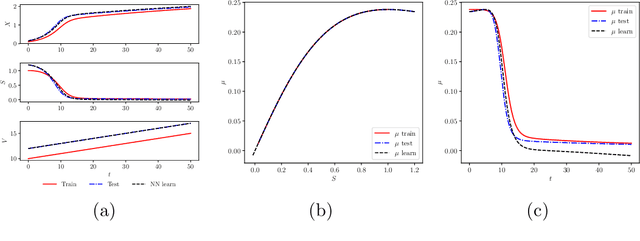
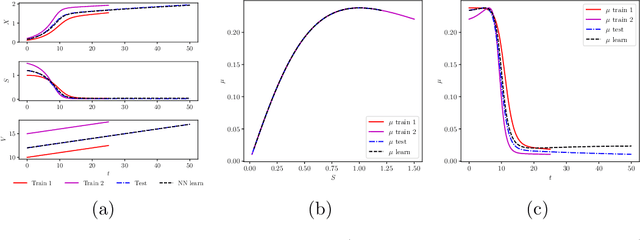
We investigate the use of discrete and continuous versions of physics-informed neural network methods for learning unknown dynamics or constitutive relations of a dynamical system. For the case of unknown dynamics, we represent all the dynamics with a deep neural network (DNN). When the dynamics of the system are known up to the specification of constitutive relations (that can depend on the state of the system), we represent these constitutive relations with a DNN. The discrete versions combine classical multistep discretization methods for dynamical systems with neural network based machine learning methods. On the other hand, the continuous versions utilize deep neural networks to minimize the residual function for the continuous governing equations. We use the case of a fedbatch bioreactor system to study the effectiveness of these approaches and discuss conditions for their applicability. Our results indicate that the accuracy of the trained neural network models is much higher for the cases where we only have to learn a constitutive relation instead of the whole dynamics. This finding corroborates the well-known fact from scientific computing that building as much structural information is available into an algorithm can enhance its efficiency and/or accuracy.