Physics-Informed Gaussian Process Regression for Probabilistic States Estimation and Forecasting in Power Grids

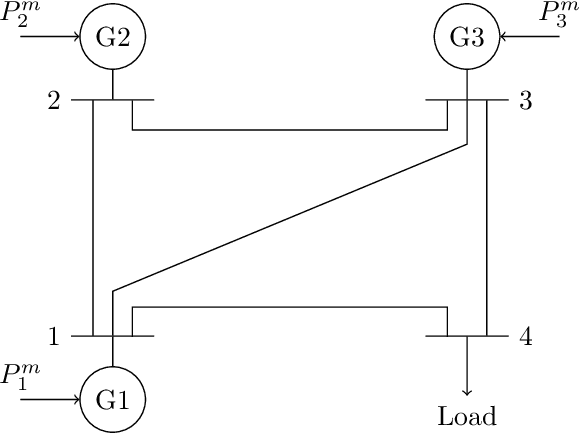
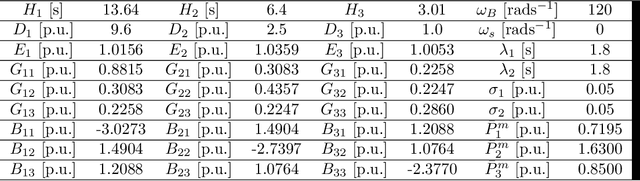
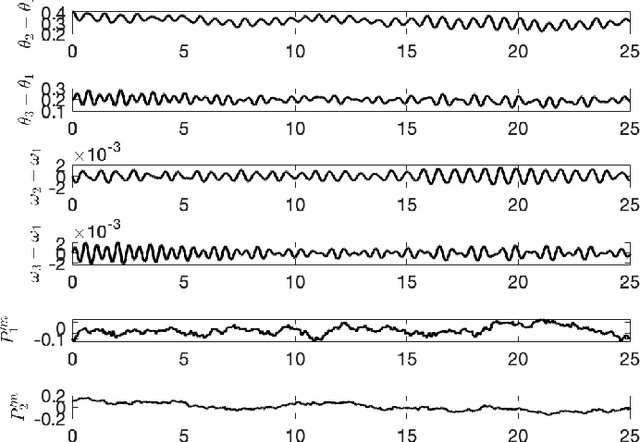
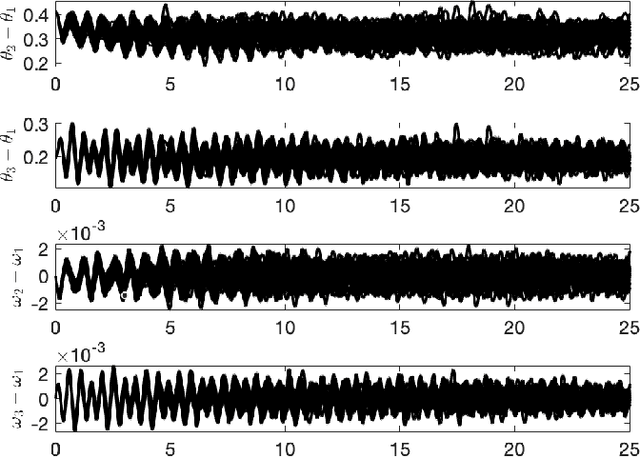
Real-time state estimation and forecasting is critical for efficient operation of power grids. In this paper, a physics-informed Gaussian process regression (PhI-GPR) method is presented and used for probabilistic forecasting and estimating the phase angle, angular speed, and wind mechanical power of a three-generator power grid system using sparse measurements. In standard data-driven Gaussian process regression (GPR), parameterized models for the prior statistics are fit by maximizing the marginal likelihood of observed data, whereas in PhI-GPR, we compute the prior statistics by solving stochastic equations governing power grid dynamics. The short-term forecast of a power grid system dominated by wind generation is complicated by the stochastic nature of the wind and the resulting uncertain mechanical wind power. Here, we assume that the power-grid dynamic is governed by the swing equations, and we treat the unknown terms in the swing equations (specifically, the mechanical wind power) as random processes, which turns these equations into stochastic differential equations. We solve these equations for the mean and variance of the power grid system using the Monte Carlo simulations method. We demonstrate that the proposed PhI-GPR method can accurately forecast and estimate both observed and unobserved states, including the mean behavior and associated uncertainty. For observed states, we show that PhI-GPR provides a forecast comparable to the standard data-driven GPR, with both forecasts being significantly more accurate than the autoregressive integrated moving average (ARIMA) forecast. We also show that the ARIMA forecast is much more sensitive to observation frequency and measurement errors than the PhI-GPR forecast.

Dynamic mode decomposition for forecasting and analysis of power grid load data

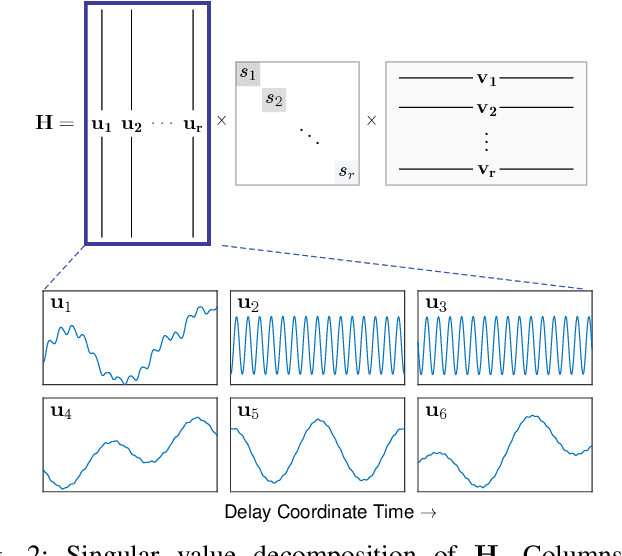
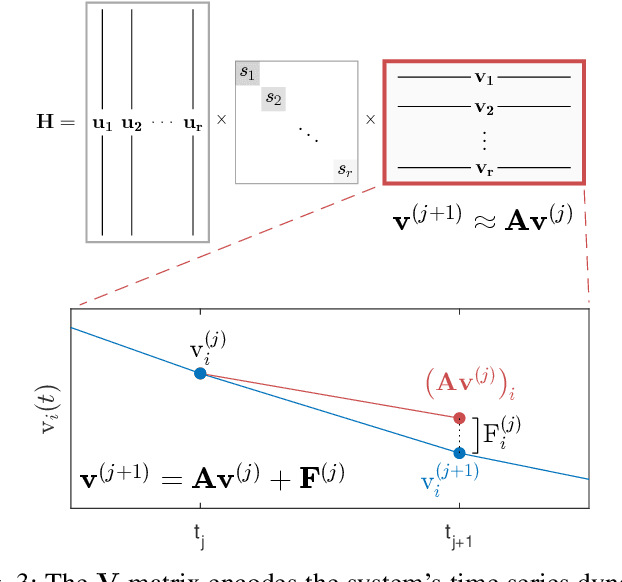
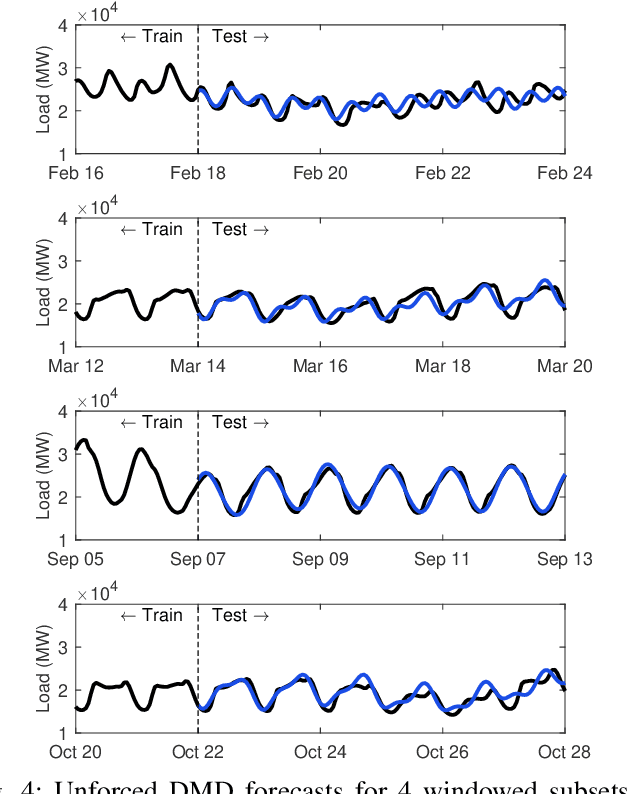
Time series forecasting remains a central challenge problem in almost all scientific disciplines, including load modeling in power systems engineering. The ability to produce accurate forecasts has major implications for real-time control, pricing, maintenance, and security decisions. We introduce a novel load forecasting method in which observed dynamics are modeled as a forced linear system using Dynamic Mode Decomposition (DMD) in time delay coordinates. Central to this approach is the insight that grid load, like many observables on complex real-world systems, has an "almost-periodic" character, i.e., a continuous Fourier spectrum punctuated by dominant peaks, which capture regular (e.g., daily or weekly) recurrences in the dynamics. The forecasting method presented takes advantage of this property by (i) regressing to a deterministic linear model whose eigenspectrum maps onto those peaks, and (ii) simultaneously learning a stochastic Gaussian process regression (GPR) process to actuate this system. Our forecasting algorithm is compared against state-of-the-art forecasting techniques not using additional explanatory variables and is shown to produce superior performance. Moreover, its use of linear intrinsic dynamics offers a number of desirable properties in terms of interpretability and parsimony.

Electric Load and Power Forecasting Using Ensemble Gaussian Process Regression

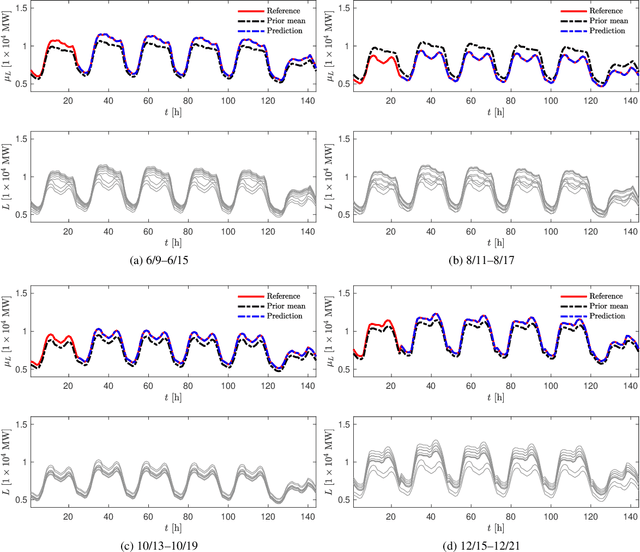
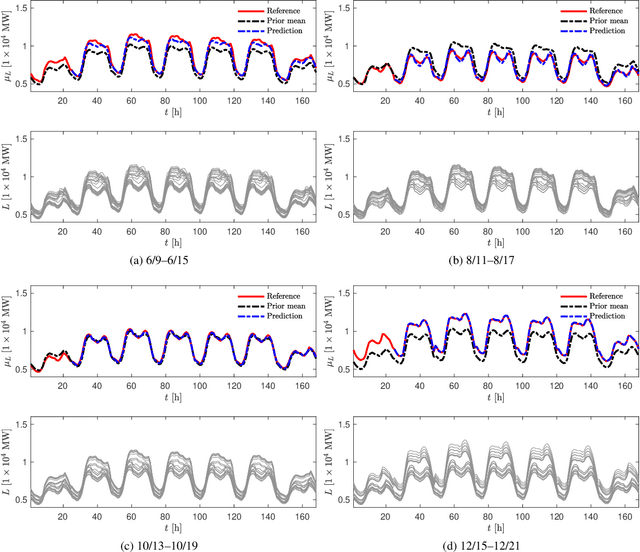
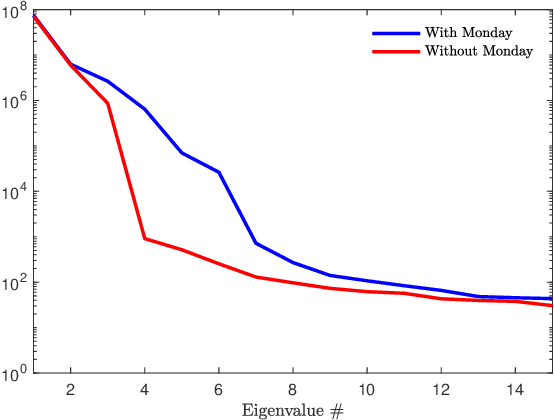
We propose a new forecasting method for predicting load demand and generation scheduling. Accurate week-long forecasting of load demand and optimal power generation is critical for efficient operation of power grid systems. In this work, we use a synthetic data set describing a power grid with 700 buses and 134 generators over a 365-days period with data synthetically generated at an hourly rate. The proposed approach for week-long forecasting is based on the Gaussian process regression (GPR) method, with prior covariance matrices of the quantities of interest (QoI) computed from ensembles formed by up to twenty preceding weeks of QoI observations. Then, we use these covariances within the GPR framework to forecast the QoIs for the following week. We demonstrate that the the proposed ensemble GPR (EGPR) method is capable of accurately forecasting weekly total load demand and power generation profiles. The EGPR method is shown to outperform traditional forecasting methods including the standard GPR and autoregressive integrated moving average (ARIMA) methods.