Dynamic mode decomposition for forecasting and analysis of power grid load data

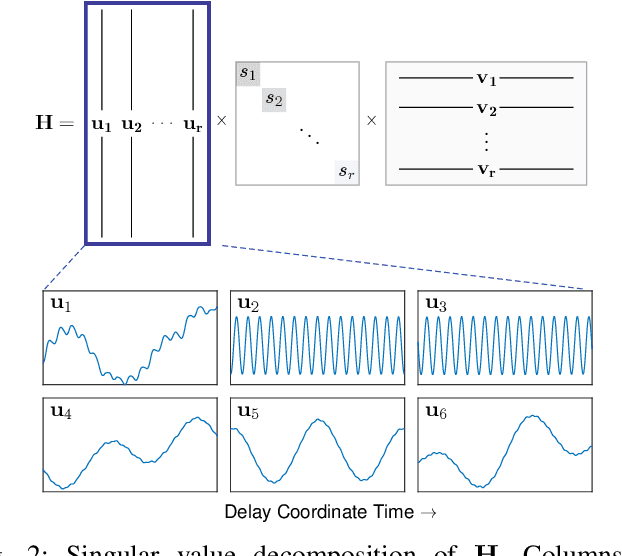
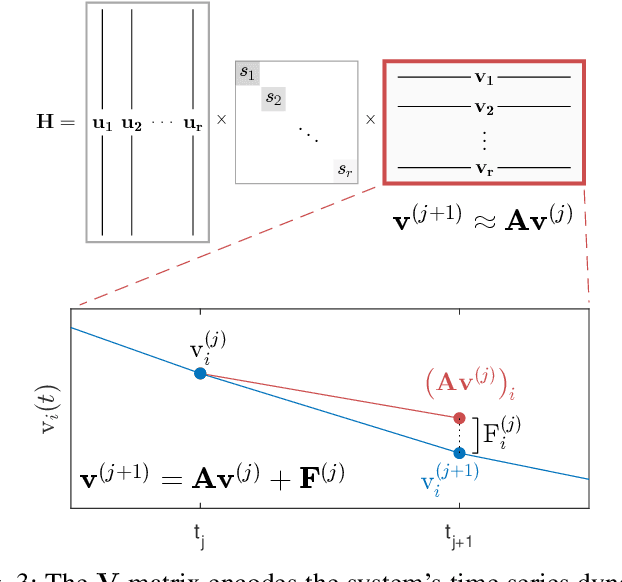
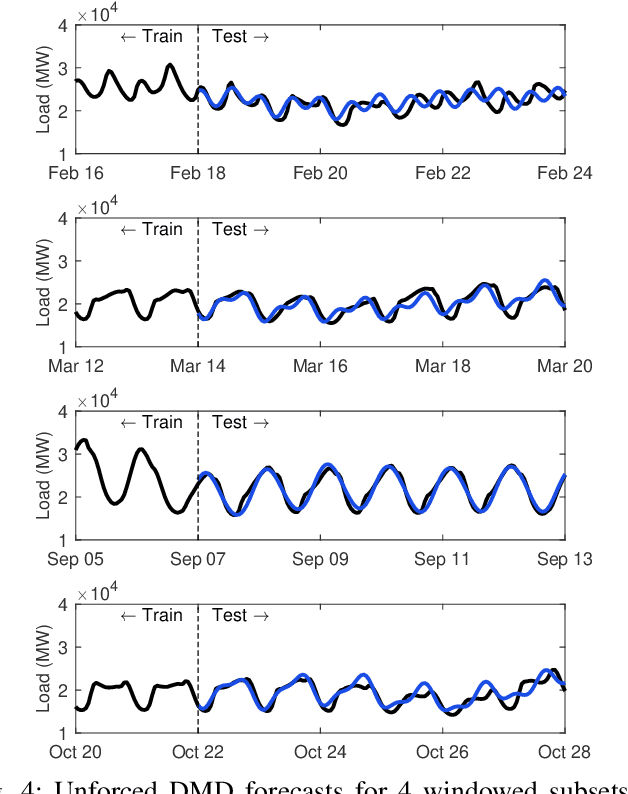
Time series forecasting remains a central challenge problem in almost all scientific disciplines, including load modeling in power systems engineering. The ability to produce accurate forecasts has major implications for real-time control, pricing, maintenance, and security decisions. We introduce a novel load forecasting method in which observed dynamics are modeled as a forced linear system using Dynamic Mode Decomposition (DMD) in time delay coordinates. Central to this approach is the insight that grid load, like many observables on complex real-world systems, has an "almost-periodic" character, i.e., a continuous Fourier spectrum punctuated by dominant peaks, which capture regular (e.g., daily or weekly) recurrences in the dynamics. The forecasting method presented takes advantage of this property by (i) regressing to a deterministic linear model whose eigenspectrum maps onto those peaks, and (ii) simultaneously learning a stochastic Gaussian process regression (GPR) process to actuate this system. Our forecasting algorithm is compared against state-of-the-art forecasting techniques not using additional explanatory variables and is shown to produce superior performance. Moreover, its use of linear intrinsic dynamics offers a number of desirable properties in terms of interpretability and parsimony.