VAE-DNN: Energy-Efficient Trainable-by-Parts Surrogate Model For Parametric Partial Differential Equations

We propose a trainable-by-parts surrogate model for solving forward and inverse parameterized nonlinear partial differential equations. Like several other surrogate and operator learning models, the proposed approach employs an encoder to reduce the high-dimensional input $y(\bm{x})$ to a lower-dimensional latent space, $\bm\mu_{\bm\phi_y}$. Then, a fully connected neural network is used to map $\bm\mu_{\bm\phi_y}$ to the latent space, $\bm\mu_{\bm\phi_h}$, of the PDE solution $h(\bm{x},t)$. Finally, a decoder is utilized to reconstruct $h(\bm{x},t)$. The innovative aspect of our model is its ability to train its three components independently. This approach leads to a substantial decrease in both the time and energy required for training when compared to leading operator learning models such as FNO and DeepONet. The separable training is achieved by training the encoder as part of the variational autoencoder (VAE) for $y(\bm{x})$ and the decoder as part of the $h(\bm{x},t)$ VAE. We refer to this model as the VAE-DNN model. VAE-DNN is compared to the FNO and DeepONet models for obtaining forward and inverse solutions to the nonlinear diffusion equation governing groundwater flow in an unconfined aquifer. Our findings indicate that VAE-DNN not only demonstrates greater efficiency but also delivers superior accuracy in both forward and inverse solutions compared to the FNO and DeepONet models.

Total Uncertainty Quantification in Inverse PDE Solutions Obtained with Reduced-Order Deep Learning Surrogate Models

We propose an approximate Bayesian method for quantifying the total uncertainty in inverse PDE solutions obtained with machine learning surrogate models, including operator learning models. The proposed method accounts for uncertainty in the observations and PDE and surrogate models. First, we use the surrogate model to formulate a minimization problem in the reduced space for the maximum a posteriori (MAP) inverse solution. Then, we randomize the MAP objective function and obtain samples of the posterior distribution by minimizing different realizations of the objective function. We test the proposed framework by comparing it with the iterative ensemble smoother and deep ensembling methods for a non-linear diffusion equation with an unknown space-dependent diffusion coefficient. Among other problems, this equation describes groundwater flow in an unconfined aquifer. Depending on the training dataset and ensemble sizes, the proposed method provides similar or more descriptive posteriors of the parameters and states than the iterative ensemble smoother method. Deep ensembling underestimates uncertainty and provides less informative posteriors than the other two methods.

Randomized Physics-Informed Neural Networks for Bayesian Data Assimilation

We propose a randomized physics-informed neural network (PINN) or rPINN method for uncertainty quantification in inverse partial differential equation (PDE) problems with noisy data. This method is used to quantify uncertainty in the inverse PDE PINN solutions. Recently, the Bayesian PINN (BPINN) method was proposed, where the posterior distribution of the PINN parameters was formulated using the Bayes' theorem and sampled using approximate inference methods such as the Hamiltonian Monte Carlo (HMC) and variational inference (VI) methods. In this work, we demonstrate that HMC fails to converge for non-linear inverse PDE problems. As an alternative to HMC, we sample the distribution by solving the stochastic optimization problem obtained by randomizing the PINN loss function. The effectiveness of the rPINN method is tested for linear and non-linear Poisson equations, and the diffusion equation with a high-dimensional space-dependent diffusion coefficient. The rPINN method provides informative distributions for all considered problems. For the linear Poisson equation, HMC and rPINN produce similar distributions, but rPINN is on average 27 times faster than HMC. For the non-linear Poison and diffusion equations, the HMC method fails to converge because a single HMC chain cannot sample multiple modes of the posterior distribution of the PINN parameters in a reasonable amount of time.

Randomized Physics-Informed Machine Learning for Uncertainty Quantification in High-Dimensional Inverse Problems

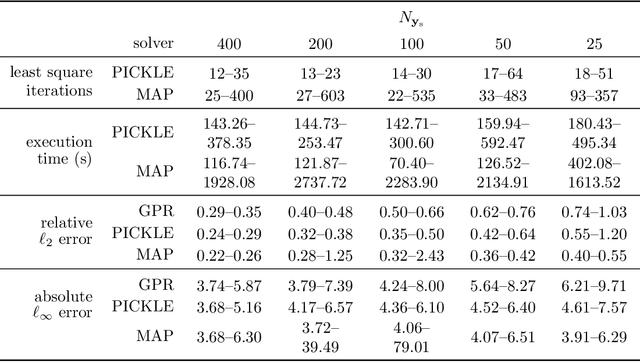
We propose a physics-informed machine learning method for uncertainty quantification in high-dimensional inverse problems. In this method, the states and parameters of partial differential equations (PDEs) are approximated with truncated conditional Karhunen-Lo\`eve expansions (CKLEs), which, by construction, match the measurements of the respective variables. The maximum a posteriori (MAP) solution of the inverse problem is formulated as a minimization problem over CKLE coefficients where the loss function is the sum of the norm of PDE residuals and the $\ell_2$ regularization term. This MAP formulation is known as the physics-informed CKLE (PICKLE) method. Uncertainty in the inverse solution is quantified in terms of the posterior distribution of CKLE coefficients, and we sample the posterior by solving a randomized PICKLE minimization problem, formulated by adding zero-mean Gaussian perturbations in the PICKLE loss function. We call the proposed approach the randomized PICKLE (rPICKLE) method. For linear and low-dimensional nonlinear problems (15 CKLE parameters), we show analytically and through comparison with Hamiltonian Monte Carlo (HMC) that the rPICKLE posterior converges to the true posterior given by the Bayes rule. For high-dimensional non-linear problems with 2000 CKLE parameters, we numerically demonstrate that rPICKLE posteriors are highly informative--they provide mean estimates with an accuracy comparable to the estimates given by the MAP solution and the confidence interval that mostly covers the reference solution. We are not able to obtain the HMC posterior to validate rPICKLE's convergence to the true posterior due to the HMC's prohibitive computational cost for the considered high-dimensional problems. Our results demonstrate the advantages of rPICKLE over HMC for approximately sampling high-dimensional posterior distributions subject to physics constraints.

Conditional Korhunen-Loéve regression model with Basis Adaptation for high-dimensional problems: uncertainty quantification and inverse modeling

We propose a methodology for improving the accuracy of surrogate models of the observable response of physical systems as a function of the systems' spatially heterogeneous parameter fields with applications to uncertainty quantification and parameter estimation in high-dimensional problems. Practitioners often formulate finite-dimensional representations of spatially heterogeneous parameter fields using truncated unconditional Karhunen-Lo\'{e}ve expansions (KLEs) for a certain choice of unconditional covariance kernel and construct surrogate models of the observable response with respect to the random variables in the KLE. When direct measurements of the parameter fields are available, we propose improving the accuracy of these surrogate models by representing the parameter fields via conditional Karhunen-Lo\'{e}ve expansions (CKLEs). CKLEs are constructed by conditioning the covariance kernel of the unconditional expansion on the direct measurements via Gaussian process regression and then truncating the corresponding KLE. We apply the proposed methodology to constructing surrogate models via the Basis Adaptation (BA) method of the stationary hydraulic head response, measured at spatially discrete observation locations, of a groundwater flow model of the Hanford Site, as a function of the 1,000-dimensional representation of the model's log-transmissivity field. We find that BA surrogate models of the hydraulic head based on CKLEs are more accurate than BA surrogate models based on unconditional expansions for forward uncertainty quantification tasks. Furthermore, we find that inverse estimates of the hydraulic transmissivity field computed using CKLE-based BA surrogate models are more accurate than those computed using unconditional BA surrogate models.

Gaussian process regression and conditional Karhunen-Loéve models for data assimilation in inverse problems

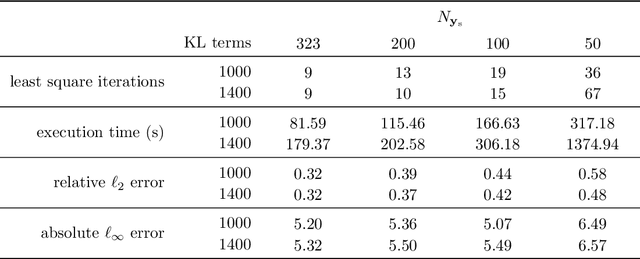
We present a model inversion algorithm, CKLEMAP, for data assimilation and parameter estimation in partial differential equation models of physical systems with spatially heterogeneous parameter fields. These fields are approximated using low-dimensional conditional Karhunen-Lo\'{e}ve expansions, which are constructed using Gaussian process regression models of these fields trained on the parameters' measurements. We then assimilate measurements of the state of the system and compute the maximum a posteriori estimate of the CKLE coefficients by solving a nonlinear least-squares problem. When solving this optimization problem, we efficiently compute the Jacobian of the vector objective by exploiting the sparsity structure of the linear system of equations associated with the forward solution of the physics problem. The CKLEMAP method provides better scalability compared to the standard MAP method. In the MAP method, the number of unknowns to be estimated is equal to the number of elements in the numerical forward model. On the other hand, in CKLEMAP, the number of unknowns (CKLE coefficients) is controlled by the smoothness of the parameter field and the number of measurements, and is in general much smaller than the number of discretization nodes, which leads to a significant reduction of computational cost with respect to the standard MAP method. To show its advantage in scalability, we apply CKLEMAP to estimate the transmissivity field in a two-dimensional steady-state subsurface flow model of the Hanford Site by assimilating synthetic measurements of transmissivity and hydraulic head. We find that the execution time of CKLEMAP scales nearly linearly as $N^{1.33}$, where $N$ is the number of discretization nodes, while the execution time of standard MAP scales as $N^{2.91}$. The CKLEMAP method improved execution time without sacrificing accuracy when compared to the standard MAP.

Physics-Informed Neural Network Method for Parabolic Differential Equations with Sharply Perturbed Initial Conditions

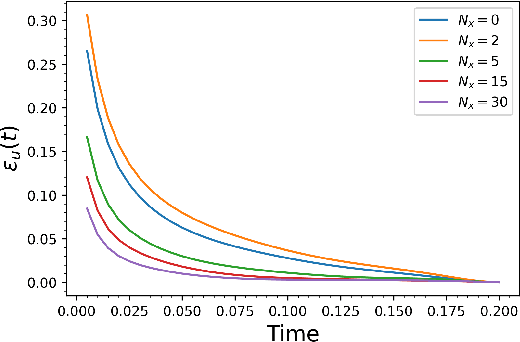
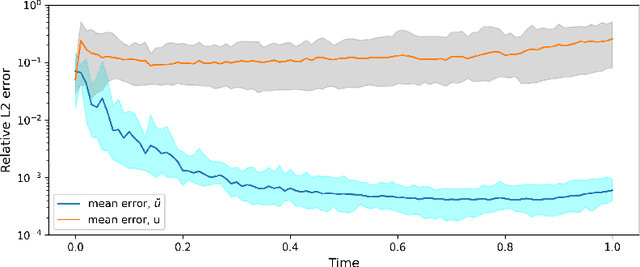
In this paper, we develop a physics-informed neural network (PINN) model for parabolic problems with a sharply perturbed initial condition. As an example of a parabolic problem, we consider the advection-dispersion equation (ADE) with a point (Gaussian) source initial condition. In the $d$-dimensional ADE, perturbations in the initial condition decay with time $t$ as $t^{-d/2}$, which can cause a large approximation error in the PINN solution. Localized large gradients in the ADE solution make the (common in PINN) Latin hypercube sampling of the equation's residual highly inefficient. Finally, the PINN solution of parabolic equations is sensitive to the choice of weights in the loss function. We propose a normalized form of ADE where the initial perturbation of the solution does not decrease in amplitude and demonstrate that this normalization significantly reduces the PINN approximation error. We propose criteria for weights in the loss function that produce a more accurate PINN solution than those obtained with the weights selected via other methods. Finally, we proposed an adaptive sampling scheme that significantly reduces the PINN solution error for the same number of the sampling (residual) points. We demonstrate the accuracy of the proposed PINN model for forward, inverse, and backward ADEs.

Physics-Informed Machine Learning Method for Large-Scale Data Assimilation Problems

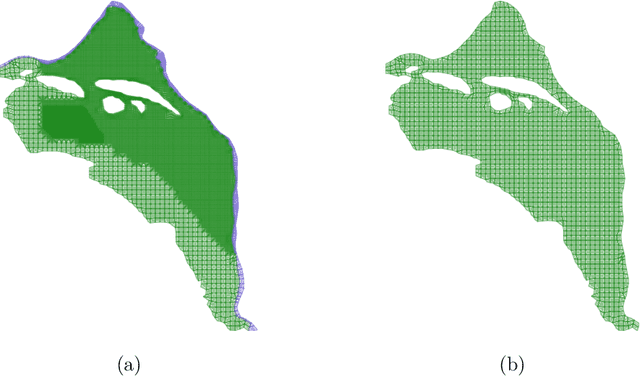
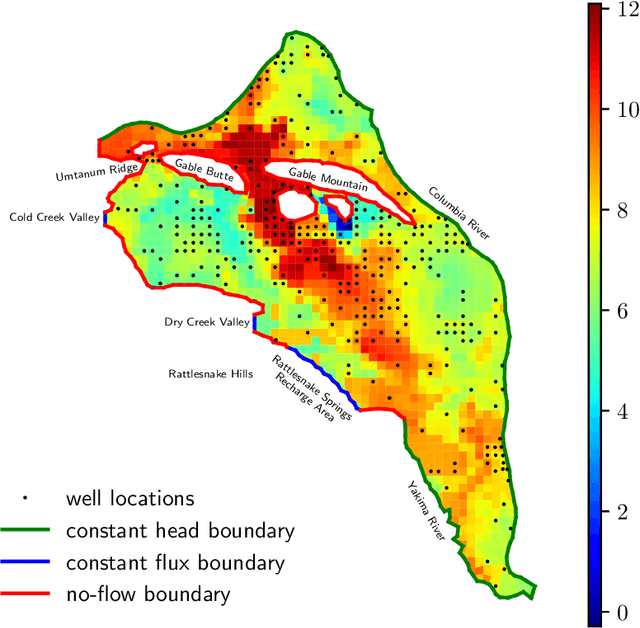
We develop a physics-informed machine learning approach for large-scale data assimilation and parameter estimation and apply it for estimating transmissivity and hydraulic head in the two-dimensional steady-state subsurface flow model of the Hanford Site given synthetic measurements of said variables. In our approach, we extend the physics-informed conditional Karhunen-Lo\'{e}ve expansion (PICKLE) method for modeling subsurface flow with unknown flux (Neumann) and varying head (Dirichlet) boundary conditions. We demonstrate that the PICKLE method is comparable in accuracy with the standard maximum a posteriori (MAP) method, but is significantly faster than MAP for large-scale problems. Both methods use a mesh to discretize the computational domain. In MAP, the parameters and states are discretized on the mesh; therefore, the size of the MAP parameter estimation problem directly depends on the mesh size. In PICKLE, the mesh is used to evaluate the residuals of the governing equation, while the parameters and states are approximated by the truncated conditional Karhunen-Lo\'{e}ve expansions with the number of parameters controlled by the smoothness of the parameter and state fields, and not by the mesh size. For a considered example, we demonstrate that the computational cost of PICKLE increases near linearly (as $N_{FV}^{1.15}$) with the number of grid points $N_{FV}$, while that of MAP increases much faster as $N_{FV}^{3.28}$. We demonstrated that once trained for one set of Dirichlet boundary conditions (i.e., one river stage), the PICKLE method provides accurate estimates of the hydraulic head for any value of the Dirichlet boundary conditions (i.e., for any river stage).

Physics-informed CoKriging model of a redox flow battery

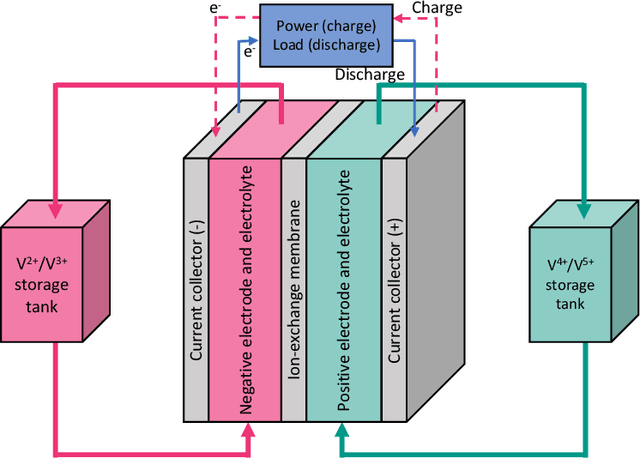
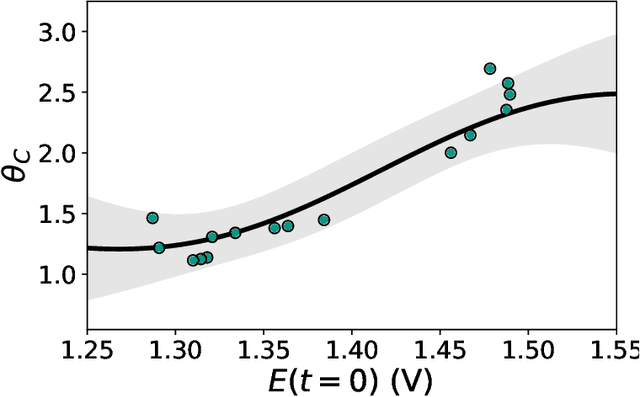
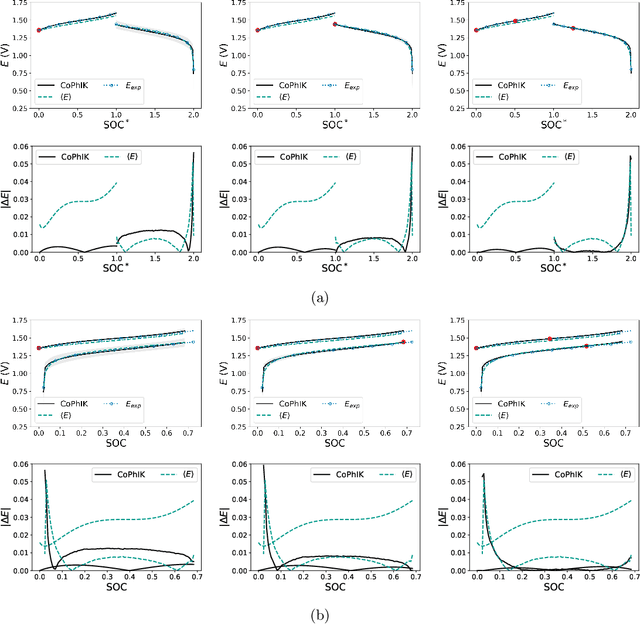
Redox flow batteries (RFBs) offer the capability to store large amounts of energy cheaply and efficiently, however, there is a need for fast and accurate models of the charge-discharge curve of a RFB to potentially improve the battery capacity and performance. We develop a multifidelity model for predicting the charge-discharge curve of a RFB. In the multifidelity model, we use the Physics-informed CoKriging (CoPhIK) machine learning method that is trained on experimental data and constrained by the so-called "zero-dimensional" physics-based model. Here we demonstrate that the model shows good agreement with experimental results and significant improvements over existing zero-dimensional models. We show that the proposed model is robust as it is not sensitive to the input parameters in the zero-dimensional model. We also show that only a small amount of high-fidelity experimental datasets are needed for accurate predictions for the range of considered input parameters, which include current density, flow rate, and initial concentrations.

Physics-Informed Gaussian Process Regression for Probabilistic States Estimation and Forecasting in Power Grids

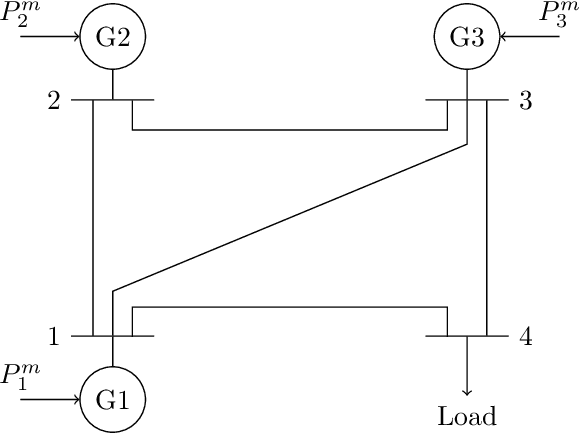
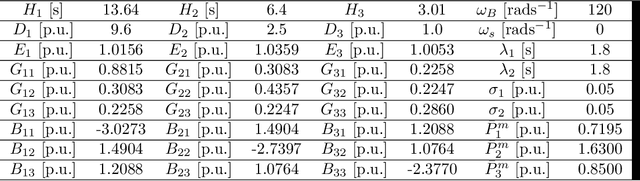
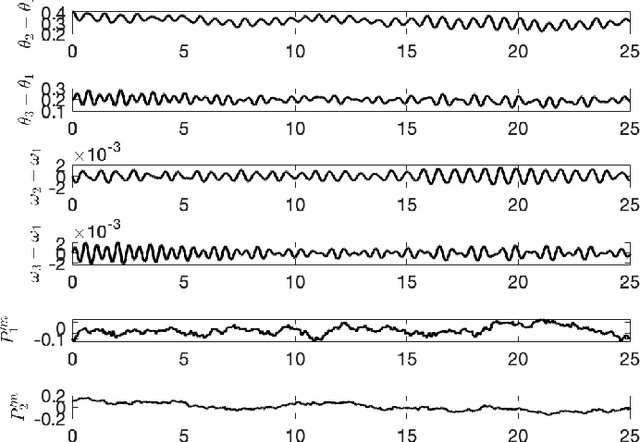
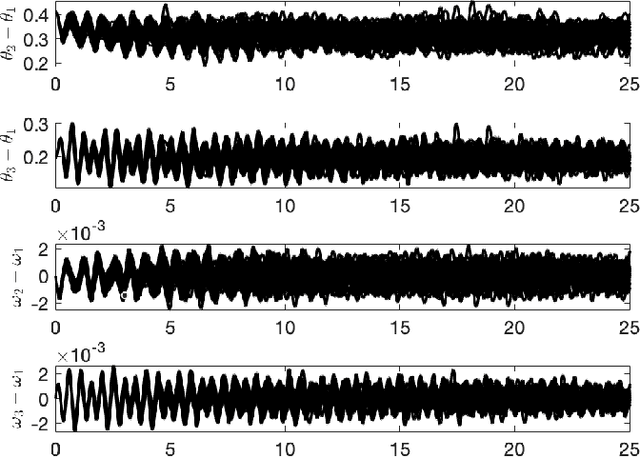
Real-time state estimation and forecasting is critical for efficient operation of power grids. In this paper, a physics-informed Gaussian process regression (PhI-GPR) method is presented and used for probabilistic forecasting and estimating the phase angle, angular speed, and wind mechanical power of a three-generator power grid system using sparse measurements. In standard data-driven Gaussian process regression (GPR), parameterized models for the prior statistics are fit by maximizing the marginal likelihood of observed data, whereas in PhI-GPR, we compute the prior statistics by solving stochastic equations governing power grid dynamics. The short-term forecast of a power grid system dominated by wind generation is complicated by the stochastic nature of the wind and the resulting uncertain mechanical wind power. Here, we assume that the power-grid dynamic is governed by the swing equations, and we treat the unknown terms in the swing equations (specifically, the mechanical wind power) as random processes, which turns these equations into stochastic differential equations. We solve these equations for the mean and variance of the power grid system using the Monte Carlo simulations method. We demonstrate that the proposed PhI-GPR method can accurately forecast and estimate both observed and unobserved states, including the mean behavior and associated uncertainty. For observed states, we show that PhI-GPR provides a forecast comparable to the standard data-driven GPR, with both forecasts being significantly more accurate than the autoregressive integrated moving average (ARIMA) forecast. We also show that the ARIMA forecast is much more sensitive to observation frequency and measurement errors than the PhI-GPR forecast.