VAE-DNN: Energy-Efficient Trainable-by-Parts Surrogate Model For Parametric Partial Differential Equations

We propose a trainable-by-parts surrogate model for solving forward and inverse parameterized nonlinear partial differential equations. Like several other surrogate and operator learning models, the proposed approach employs an encoder to reduce the high-dimensional input $y(\bm{x})$ to a lower-dimensional latent space, $\bm\mu_{\bm\phi_y}$. Then, a fully connected neural network is used to map $\bm\mu_{\bm\phi_y}$ to the latent space, $\bm\mu_{\bm\phi_h}$, of the PDE solution $h(\bm{x},t)$. Finally, a decoder is utilized to reconstruct $h(\bm{x},t)$. The innovative aspect of our model is its ability to train its three components independently. This approach leads to a substantial decrease in both the time and energy required for training when compared to leading operator learning models such as FNO and DeepONet. The separable training is achieved by training the encoder as part of the variational autoencoder (VAE) for $y(\bm{x})$ and the decoder as part of the $h(\bm{x},t)$ VAE. We refer to this model as the VAE-DNN model. VAE-DNN is compared to the FNO and DeepONet models for obtaining forward and inverse solutions to the nonlinear diffusion equation governing groundwater flow in an unconfined aquifer. Our findings indicate that VAE-DNN not only demonstrates greater efficiency but also delivers superior accuracy in both forward and inverse solutions compared to the FNO and DeepONet models.

Mathematics of Digital Twins and Transfer Learning for PDE Models

We define a digital twin (DT) of a physical system governed by partial differential equations (PDEs) as a model for real-time simulations and control of the system behavior under changing conditions. We construct DTs using the Karhunen-Lo\`{e}ve Neural Network (KL-NN) surrogate model and transfer learning (TL). The surrogate model allows fast inference and differentiability with respect to control parameters for control and optimization. TL is used to retrain the model for new conditions with minimal additional data. We employ the moment equations to analyze TL and identify parameters that can be transferred to new conditions. The proposed analysis also guides the control variable selection in DT to facilitate efficient TL. For linear PDE problems, the non-transferable parameters in the KL-NN surrogate model can be exactly estimated from a single solution of the PDE corresponding to the mean values of the control variables under new target conditions. Retraining an ML model with a single solution sample is known as one-shot learning, and our analysis shows that the one-shot TL is exact for linear PDEs. For nonlinear PDE problems, transferring of any parameters introduces errors. For a nonlinear diffusion PDE model, we find that for a relatively small range of control variables, some surrogate model parameters can be transferred without introducing a significant error, some can be approximately estimated from the mean-field equation, and the rest can be found using a linear residual least square problem or an ordinary linear least square problem if a small labeled dataset for new conditions is available. The former approach results in a one-shot TL while the latter approach is an example of a few-shot TL. Both methods are approximate for the nonlinear PDEs.

Randomized Physics-Informed Neural Networks for Bayesian Data Assimilation

We propose a randomized physics-informed neural network (PINN) or rPINN method for uncertainty quantification in inverse partial differential equation (PDE) problems with noisy data. This method is used to quantify uncertainty in the inverse PDE PINN solutions. Recently, the Bayesian PINN (BPINN) method was proposed, where the posterior distribution of the PINN parameters was formulated using the Bayes' theorem and sampled using approximate inference methods such as the Hamiltonian Monte Carlo (HMC) and variational inference (VI) methods. In this work, we demonstrate that HMC fails to converge for non-linear inverse PDE problems. As an alternative to HMC, we sample the distribution by solving the stochastic optimization problem obtained by randomizing the PINN loss function. The effectiveness of the rPINN method is tested for linear and non-linear Poisson equations, and the diffusion equation with a high-dimensional space-dependent diffusion coefficient. The rPINN method provides informative distributions for all considered problems. For the linear Poisson equation, HMC and rPINN produce similar distributions, but rPINN is on average 27 times faster than HMC. For the non-linear Poison and diffusion equations, the HMC method fails to converge because a single HMC chain cannot sample multiple modes of the posterior distribution of the PINN parameters in a reasonable amount of time.

Randomized Physics-Informed Machine Learning for Uncertainty Quantification in High-Dimensional Inverse Problems

We propose a physics-informed machine learning method for uncertainty quantification in high-dimensional inverse problems. In this method, the states and parameters of partial differential equations (PDEs) are approximated with truncated conditional Karhunen-Lo\`eve expansions (CKLEs), which, by construction, match the measurements of the respective variables. The maximum a posteriori (MAP) solution of the inverse problem is formulated as a minimization problem over CKLE coefficients where the loss function is the sum of the norm of PDE residuals and the $\ell_2$ regularization term. This MAP formulation is known as the physics-informed CKLE (PICKLE) method. Uncertainty in the inverse solution is quantified in terms of the posterior distribution of CKLE coefficients, and we sample the posterior by solving a randomized PICKLE minimization problem, formulated by adding zero-mean Gaussian perturbations in the PICKLE loss function. We call the proposed approach the randomized PICKLE (rPICKLE) method. For linear and low-dimensional nonlinear problems (15 CKLE parameters), we show analytically and through comparison with Hamiltonian Monte Carlo (HMC) that the rPICKLE posterior converges to the true posterior given by the Bayes rule. For high-dimensional non-linear problems with 2000 CKLE parameters, we numerically demonstrate that rPICKLE posteriors are highly informative--they provide mean estimates with an accuracy comparable to the estimates given by the MAP solution and the confidence interval that mostly covers the reference solution. We are not able to obtain the HMC posterior to validate rPICKLE's convergence to the true posterior due to the HMC's prohibitive computational cost for the considered high-dimensional problems. Our results demonstrate the advantages of rPICKLE over HMC for approximately sampling high-dimensional posterior distributions subject to physics constraints.

Physics-Informed Neural Network Method for Parabolic Differential Equations with Sharply Perturbed Initial Conditions

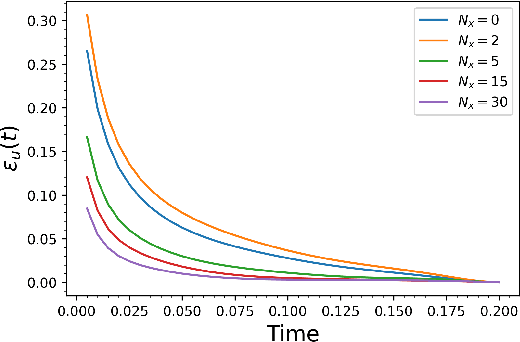
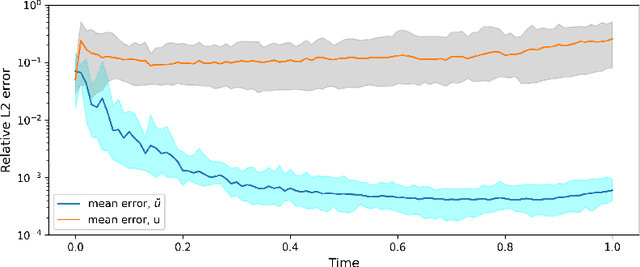
In this paper, we develop a physics-informed neural network (PINN) model for parabolic problems with a sharply perturbed initial condition. As an example of a parabolic problem, we consider the advection-dispersion equation (ADE) with a point (Gaussian) source initial condition. In the $d$-dimensional ADE, perturbations in the initial condition decay with time $t$ as $t^{-d/2}$, which can cause a large approximation error in the PINN solution. Localized large gradients in the ADE solution make the (common in PINN) Latin hypercube sampling of the equation's residual highly inefficient. Finally, the PINN solution of parabolic equations is sensitive to the choice of weights in the loss function. We propose a normalized form of ADE where the initial perturbation of the solution does not decrease in amplitude and demonstrate that this normalization significantly reduces the PINN approximation error. We propose criteria for weights in the loss function that produce a more accurate PINN solution than those obtained with the weights selected via other methods. Finally, we proposed an adaptive sampling scheme that significantly reduces the PINN solution error for the same number of the sampling (residual) points. We demonstrate the accuracy of the proposed PINN model for forward, inverse, and backward ADEs.